OLED器件壽命衰退模型的MATLAB分析計算

王憶鋒，唐利斌，岳 清

(昆明物理研究所， 昆明650223)

有機發光二極管(Organic Light Emitting Diode，OLED)是由光刻電極基板與有機發光材料構成的顯示器件，長壽命、高亮度、低功耗是OLED器件的發展方向[1-2]。驅動電壓的變化規律在某種程度上是OLED壽命衰退機制的反映。一般而言，驅動電壓隨著點亮時間的延長而增加，亮度(或電發光效率)隨時間而降低[3]。在實際測試過程中，即使電流密度恒定，驅動電壓也會發生變化。本文從計算的角度，介紹了OLED器件壽命衰退模型的MATLAB分析方法。

1 OLED驅動電壓與離子濃度的關系

通常的OLED器件壽命測試是在一定電流密度下檢測器件亮度隨點亮時間的變化關系，然后外推到器件亮度衰減至起始亮度的一半時進行評估的。一般認為OLED器件的偏置電壓引入一個與外部電場方向相反的內部極化電場，使得驅動電壓隨著點亮時間的延長而增加。引起內部極化電場的機制有若干種，其中之一是運動離子在外加偏置電壓下的重新分布[3]。

OLED中瞬態運動離子的分布及其與驅動電壓的關系可由下列方程描述[3]

式中， C(x， t)為運動離子濃度；D為擴散系數， μ為遷移率， E為電場強度；ΔV(t)為驅動電壓的變化量， q為電子電荷量， ε0為真空介電常數， εr為相對介電常數；L為OLED陰極與陽極之間的距離。

式(1)是一個線性偏微分方程，其初始條件為

另外

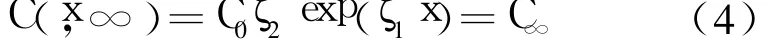
其中

粒子數守恒要求

根據上述條件，利用MATLAB提供的laplace()命令對式(1)做拉普拉斯變換，有

式(7)是一個常微分方程，調用MATLAB的dsolve()命令，可以求出

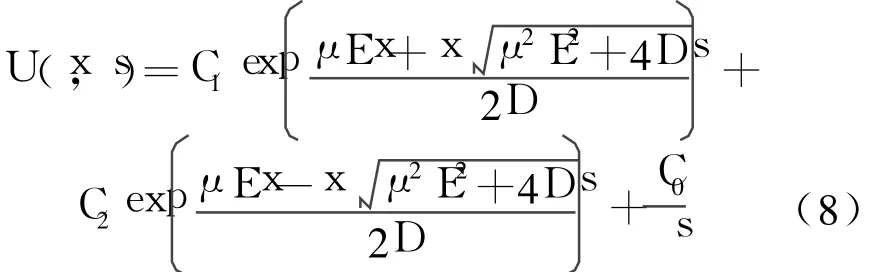
如果能求出上式的拉普拉斯逆變換，那么即可得到C(x， t)。但是利用MATLAB提供的拉普拉斯逆變換命令ilaplace()，無法求解式(8)。

如果引入變量

則式(8)可以化為

雖然可以用 ilaplace()命令求出式(10)對應的C(x， T)，但是要實現從C(x， T)→C(x， t)的轉換并不容易。事實上，利用數學物理方程理論中介紹的常見方法均無法求出該模型的解析解。

2 模型的近似求解

滿足式(3)和(4)的函數C(x， t)應該具有下列形式

其中待定函數f(ξt)要滿足條件f(0)=1， f(∞)=0。若干這樣的函數形態可以列出如下

式中， erf()為誤差函數，定義為

erfc()為余誤差函數，定義為

MATLAB中有erf()和erfc()命令可供直接調用。另外，由于負指數函數可以用有理函數近似[4]，所以實際上f(ξt)最終可歸為負指數函數和誤差函數兩種形式。

因為ξ與t之乘積應是一個無量綱的數值，故關于ξ的選取應考慮兩個因素，首先其量綱應為1/s；其次為了引入空間位置變化的影響， ξ中應包含坐標變量x。

擴散率D的量綱為cm2/s， 電場 E的量綱為V/cm，遷移率μ的量綱為cm2/V?s；故對于指數函數可以取

而對于誤差函數erf()，可以取

3 模型計算與參數擬合

將式(11)代回式(2)，可以寫出

其中

注意到在MATLAB中當f(ξt)為誤差函數時，I1和I2兩項積分不易做符號計算，故本文中選用負指數函數，即取式(15)，這時可以利用MATLAB的int()命令計算出式(19)所示的三個定積分的值，進一步整理后可得，

其中

另外，類似于在PN結IV特性曲線中的引入理想因子的做法[4-5]，在式(20)中引入三個參數α、β和γ，即

以此來描述實際測試數據與理論模型之間的偏離程度。已知測試數據后， 這三個參數容易通過調用MATLAB的最小二乘曲線擬合命令lsqcurvefit()求出[6]。

若假設OLED器件內的電場為常量，則電場E與施加的偏置電壓V及長度L之間有如下關系

將式(24)代入式(23)，可以得到ΔV(t)與不同偏壓之間的關系。

4 恒流離子源條件下模型的有限差分矩陣計算

在實際使用過程中， OLED電極材料中的離子可能會發生遷移，形成一個恒流離子源，與這種情況對應的條件是

另設初始條件仍為式(3)。在這兩個條件下，利用數學物理方法理論中介紹的各種技巧，很難求解式(1)；用試湊法也不易找到同時滿足這兩個條件的解析表達式。下面介紹基于有限差分的數值算法。

如圖1所示，在x軸方向以Δx為間距，將求解區域等間距劃分為M個區域，計有(M+1)個節點，其中邊界節點2個。設n為時間坐標，將時間坐標上的計算區域劃分為T個等份，共有(T+1)時間節點，兩個時間節點之間的間隔Δt稱為時間步長。引入時間量后的節點坐標記為Ψ(mΔx， nΔt)，省略各步長項后可寫為Ψ(m， n)，或者進一步簡記為Ψ(n)(m)。

圖1 順序排列的等間距網格節點

差分法的基本思想是在各網格節點對函數做泰勒級數展開并取近似，用差商代替導數，將偏微分方程轉化為一個線性方程組形式的差分方程，通過求解線性方程組得到微分方程的近似解。差分有不同的格式。設已知(m， n)的值。在(m， n+1)處，時間導數用向后差分近似，空間導數用中心差分近似，可得古典隱格式的差分格式。古典隱格式是絕對穩定的[7]。

具體到這里的離子濃度函數C(x， t)，在(m，n+1)處，其對坐標x的偏導數可以用(n+1)時刻的中心差分近似為

C(x， t)對時間坐標t的一階偏導數可以用(n+1)時刻的向后差分近似為

將式(26)～(28)代入式(1)，可以得到古典隱格式的差分方程

其中

對整個OLED器件結構離散化，即從m=2 開始直到m=M +1，逐點寫出式(29)；當進行到最后一個節點時，會出現標號為(M +2)的節點，這時后退一格。整理后可得下列形式的矩陣方程

式中，Γ是一個M×M階的三對角線矩陣，定義為在MATLAB中可用spdiags()命令生成Γ矩陣[8]。

C(n+1)和C(n)均為M×1階矩陣，分別定義如下C(n)為初始值或前一時刻離子濃度值及恒流離子源的數值構成的已知量， 其中對式(25)取向前差分，即

C(n+1)為待求未知量，構造出Γ矩陣和C(n)矩陣后， 利用 MATLAB的矩陣左除命令即可求出C(n+1)的值；因為計算得到的C(n+1)本身為離散值，這時利用MATLAB的樣條插值積分命令如fnint()等[6，9]，即可 計 算出(n+1)時 刻 的ΔV(t)值， 即式(2)；再將C(n+1)作為已知量代入第n+2 個時間步長計算C(n+2)的值，如此循環往復直至達到所設定的時間步長時為止。最后利用MATLAB提供的多項式擬合命令polyfit()，對各時刻得到的ΔV(t)值做擬合，可以獲得驅動電壓的變化量ΔV與時間t之間的多項式函數表達式。

5 結束語

影響OLED器件壽命的主要因素有材料的物理化學穩定性、器件結構的合理性、密封膜層的有效性、有害離子的遷移性等，多數情況下這些因素相互影響和制約，使得對于器件性能衰退機制的全面理解錯綜復雜。 OLED器件壽命衰退機制的探討可以粗略地分為兩條路徑，一條是實驗研究與分析，另一條是模型的理論計算與仿真。本文介紹的方法具有一定的普適性，可以有效地解決OLED衰退模型的計算問題；通過擬合，還可以進一步建立模型與測試數據之間的對應關系，從而將理論模型與工藝或實驗有機地聯系起來。

[ 1] 袁永波，連加容，周翔.空穴阻擋層對有機發光二極管壽命的影響[ J] .電子器件， 2008， 31(1)：25-28.

[ 2] 李大勇， 劉明.采用 Al2O3/ITO陽極的有機電致發光器件[ J] .電子器件， 2008， 31(1)：22-24.

[ 3] Shen J， Wang D， Langlois E， et al.Degradation Mechanisms in Organic Light Em itting Diodes[ J].Synthetic Metals， 2000，(111/112)：233-236.

[ 4] 王憶鋒，毛京湘.根據IV曲線形態定性判斷PN結性能的一種簡易方法[ J] .紅外， 2008， 29(4)：20-23.

[ 5] Robert F Pierret著.黃如，王漪，等譯.半導體器件基礎[ M].北京：電子工業出版社， 2004年11月.

[ 6] 薛定宇，陳陽泉.高等應用數學問題的MATLAB求解[ M] .北京：清華大學出版社， 2004年8月.

[ 7] 陸君安，尚濤，謝進，等.偏微分方程的MATLAB解法[ M] .武漢：武漢大學出版社， 2001年8月.

[ 8] 王憶鋒，唐利斌.利用有限差分和MATLAB矩陣運算直接求解二維泊松方程[ J].紅外技術， 2010， 32(4)：213-216.

[ 9] 王憶鋒，毛京湘.用MATLAB和樣條函數擬合紅外探測器相對光譜響應曲線[ J].光電技術應用， 2008， 23(2)：46-49.