一種高動態性能數字DC-DC算法建模與芯片設計*

周浬皋，李冬梅

1.清華大學微電子學研究所， 北京100084；

2.清華大學電子工程系， 北京100084

手機、掌上電腦、MP4等多媒體設備需要精度高且穩定的供電，因此會配有專門的電源管理芯片。降壓型DC-DC是電源芯片當中的主要模塊，它將隨不穩定的電池電壓轉換成基帶芯片所要求的電壓，并且在負載變化的情況下依舊能保持電壓穩定。本文采用了一種新的結構，對反饋系統進行了優化，并以手機基帶供電為背景，提出指標，完成仿真和芯片設計。

文章第1部分簡單介紹降壓型DC-DC的工作原理和重要組成模塊；第2 部分描述算法設計的思路，接下來的第3部分介紹如何用硬件實現算法構想；最后給出了仿真結果、分析和結論。

1 工作原理

降壓型DC-DC的組成如圖1所示，虛線框以上為功率電路部分，它將電源電壓轉換成負載所要求的電壓，虛線框內是反饋控制部分，它將輸出電壓穩定在要求范圍內，使其不隨電源電壓、負載大小的變化而變化。其原理是利用反饋系統，對輸出電壓進行檢測，并通過補償算法來調整輸出脈沖的占空比，從而控制1、2開關的通斷時間，繼而控制輸出電壓。公式表示中， D代表輸出脈寬的占空比[1]：

圖1 數字降壓型DC-DC原理[2]

以手機基帶芯片供電這一應用為例， Vg代表手機電池，其輸出電壓變化范圍為2.4 V到3.3 V。R相當于基帶芯片負載，它是一個隨時變化的量。輸出電壓V則是芯片所獲得的電壓。虛線框內為數字校正部分，它由模數轉換器、補償算法、數字脈沖寬度調制器三部分組成。

2 算法分析

2.1 直接數字法介紹[ 3 ～5]

對于數字控制系統，通常有兩種建模的辦法：數字映射法和直接數字法。數字映射法是指先在模擬域內考慮補償函數，然后再將其轉化為數字信號來處理；直接數字法是將所有的模擬模塊全部建模成數字信號，直接在數字域里面尋找補償函數。數字映射法可以將模擬算法映射為數字算法，這樣可以利用模擬電路的豐富積累。但如果考慮功率轉換電路的相位裕度和帶寬，以及負載的瞬態響應，直接數字法是有優勢的。一來它是在一個更保守的環境下設計系統，這樣提高了設計的可靠性；二來直接數字法能夠更方便的控制階躍響應的波形。

2.2 系統建模[ 6]

功率電路的傳輸函數為：

利用直接數字法，將整個系統進行數字建模。先假定整個環路的延遲為一個周期，并且考慮DPWM的零階抽樣保持。

2.3 補償函數的尋找

對于BULK電路，在0 db時，相位為-180°，其相位裕度接近于零，見圖2。系統不穩定，須引入補償算法。

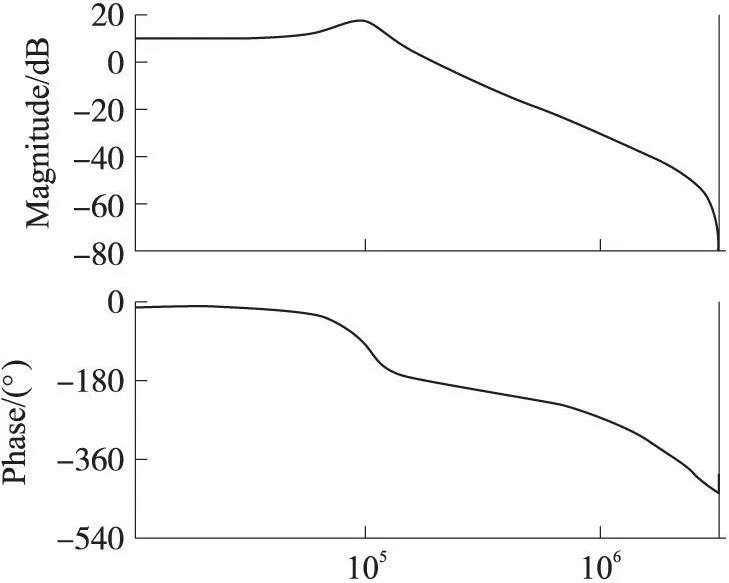
圖2 BULK電路開環波特圖

設補償算法的傳輸函數為C(z)，系統開環傳遞函數為Hop，閉環傳遞函數為Hcl。

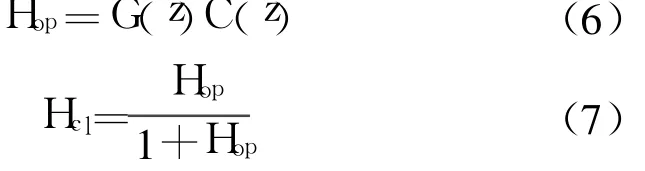
設補償函數具有如下形勢：

需要根據G(z)的特點，并且結合數字電路的可實現性，來確定補償函數零極點的個數和位置，從而使得閉環系統有良好的階躍響應。

傳統的方法是采用零極點相消，得到一個相位裕度足夠的開環波特圖，從而判斷其階躍響應。但這種方法對階躍響應的過沖、穩定時間的控制并不直觀。而利用MATLAB，在根軌跡中粗調補償零極點的位置，并且對開環波特圖進行細調，從而能夠更直接的控制階躍響應的波形，也提高了對波形精度的控制能力，使它更能貼近需求[7]。所得補償函數如下[8]：

2.4 周期個數對動態性能的影響

前面在建立系統函數的時候，假定系統在一個周期內能完成反饋。而通常的情況是輸出電壓經過模數轉換器需要一個周期，算法需要一個周期，脈寬調制器也可能增加一個周期。每增加一個周期，系統的相位裕度就會變差一些。對Z域而言，每多一個周期，就多了一個極點，這樣使得補償難度更大，階躍響應的動態性能更差。

表1對比了在此系統環境下，環路不同周期的延遲對階躍響應造成的影響。可以看出，周期的減少對動態性能與穩定性能均有較大的影響。因此本文嘗試用一個周期完成整個反饋過程。

表1 周期與階躍的關系

3 電路的實現

若要一個周期完成整個反饋運算，那么數模轉換與補償算法要在一個周期內完成，并且在下一個周期開始的那一刻，脈沖寬度調制器置為高電平，且輸出有效脈寬。系統的工作頻率為1 MHz，時序安排如圖3所示。

圖3 系統時序分配

3.1 ADC的設計

對于數字降壓型DC-DC而言，為使得輸出紋波較低(低于8 mV)，同時又不出現極限環效應， ADC的最低有效位LSB的選取應該滿足如下關系：

其中Vr為最小輸出紋波， LSB為ADC最小采樣精度，最左邊的表達式是指輸出電壓的最小調節精度， n是指pwm的位數。結合電路指標， ADC的LSB選擇為5 mV。

在DC-DC的設計中，轉換效率是很重要的指標，因此ADC的功耗不能太大。同時，由于時序的要求，需要ADC在不到一個周期的時間內產生輸出。結合這些特點， ADC采用如圖4所示的結構[9]：

圖4 ADC的結構

左邊MOS開關與采樣電容、高增益運放構成一個采樣保持電路，其指標為50 ns內建立到0.1%，因此運放的增益要求為70 dB，帶寬為150 MHz。右邊是一個低壓VCO[10-11]，其中心頻點約在1.25 V附近。此部分電路完成了對Vo信號的采樣，后面接計數器，將模擬量數字化，并完成校正和做差。

整個ADC的工作原理是，前50 ns采樣，然后用450 ns讓VCO起振，計數器記下VCO的震蕩個數，然后與預置的標準數做差，從而得出Vo與Vref誤差的數字輸出，見圖5 。

圖5 ADC的算法

3.2 算法的設計

在任何閉環系統的設計當中，開環增益是極其重要的參數，它直接影響反饋系統的穩定性以及建立精度。在DC-DC設計當中，最難的問題是確定系統的開環增益。整個環路中包括開關、ADC、PWM等模塊，因此不能簡單的認為補償函數與功率函數的總增益便是開環增益。目前尚沒有精確的理論分析來給出開環增益的推導過程，只好另辟途徑，采用測試的辦法。

在整個系統搭建起來之后，將系統在Vo與ADC的連接處斷開，并設補償函數的增益為1。在ADC的輸入端加入一個合適的電壓差量，并測量輸出Vo的值，相比得到的增益，便是算法增益歸一時的環路增益。將算法增益代入，便能得到整個系統的開環增益。

考慮一個周期的延遲，將補償函數轉化為差分方程：

3.3 DPWM的設計

這里需要一個10位的數字脈沖調制器(DPWM)，脈寬的變化范圍是0 ns到1 023 ns，每個數值對應1 ns。傳統的結構是用32個的延遲單元構成低5位的延遲，然后再用一個5位的計數器，來實現高5位的延遲[12]。考慮功耗、面積等因素，本文依然沿用這一結構，但這一結構由于包含了豐富的數字電路，而脈寬最小單位為1 ns，因此容易產生競爭，尤其是在極小或極大輸出脈寬的情況下， RS觸發器無法正常啟動或復位，從而導致輸出脈寬產生根本性的誤差[13]。

考慮到輸出電壓一般是穩定在Vref附近，因此占空比在Vref/Vo附近的精度要求是最高的，而對于兩個極端情況，其精度對系統的影響可以忽略。因此，在算法部分，將容易使DPWM產生沖突的數值濾除掉，從而在不影響系統性能的情況下，極大的增加了系統的穩定性[14]。

4 結果分析

圖6所示是芯片的后仿結果，由圖可知，當負載從50 mA跳變到800 mA時，電路能夠在140 μs內穩定到1.25 V附近，紋波不超過5 mV，穩定的精度能達到0.5%。

圖6 仿真結果

實際電路仿真已取得良好的動態性能以及較高的建立精度，但與系統函數的仿真結果仍有少許差距：在負載跳變時，會出現短時間的震蕩。這主要是因為，在將系統數字化實現時，出現了參數量化、有限字長、高階極限環等效應的影響[15]。若要減少這些效應的影響，需要增加量化的精度，乘法器的位數等，這樣系統芯片的面積、功耗等開銷會有所增加。在實際應用中，可以根據情況進行折中。

[ 1] RobertW Erickson， Dragan Maksimovic.Fundamentals of Power Electronics SECOND EDITION[ M] .Page(s)， 37-61.

[ 2] 孟浩.數字控制DC-DC開關電源研究[ D] .清華大學碩士學位論文， 2007.

[ 3]Peng H， Prodic A.Modeling of Quantization Effects in Digitally Controlled DC-DCConverters[ J] .IEEE Transactionson Power Electronics， 22(1)：208-215.

[ 4] Lukic Z， Rahman N.MultibitΣ– PWM Digital Controller IC for DC-DCConverters Operating at Switching Frequencies beyond 10MH[ J].IEEE Transactions on Power Electronics， 22(5)：1693-1707.

[ 5] A larcon E， Pao L.Proximate Time-Optimal Digital Control for DCDCConverters For Peer Review[ J] .IEEE Transactions on Power ElectronicsManuscript ID：TPEL-2007-07-0343 Manuscript Type：Regular Paper.

[ 6] Trevisan D， PMattavelli.Digital ControlofSingle-InductorMultiple-Output Step-Down DC–DCConverters in CCM.IEEE Transactions on Industrial Electronics， 55(9)：3476-3483.

[ 7]Franklin G F， Powell JD， Workman M.Digital Control of Dynamic Systems[ M] .北京，清華大學出版社， 2001， 222-238.

[ 8] Bryant B， Kazimierczuk M.Voltage Loop ofBoost PWM DC-DCConverterswith Peak Current-Mode Control[ J].IEEE Transactions on Circuits and Systems Part 1：Regular Papers， 53(1)：99-105.

[ 9] Chui Martin YeungKei， Ki W ingHung， Tsui ChiY ing.An Integrated Digital Controller for DC-DCSwitching Converterwith Dual-Band Switching[ C] //2003 Svmposium on VLSl Circuits Digest of Technical Papers.

[ 10] Straayer M， Perrott M.A 12-Bit， 10-MHz Bandwidth， Continuous-Time SigmaDelta ADC with a 5-Bit， 950-MS/s VCOBased Quantizer.IEEE Journal of Solid-State Circuits， 43(4)：805-814.

[ 11] Wei P， Min P.Design of New CMOSQuadrature VCO[ J] .Chinese Journal of Electron Devices.

[ 12] Abram Dancy， Anantha Chandrakasan.A Reconfigurable Dual Output Low Power Digital PWM Power Converter[ J] .Low Power Electronics and Design， 1998， Page(s)：191-196.

[ 13] Choe S， Ahn J.Dynam ic Simulator for a PEM Fuel Cell System with a PWM DC/DC Converter[ J] .IEEE Transactions on Energy Conversion， 23(2)：669.

[ 14] Lukic Z， Wang K.Multibit 6 0 1 PWM Digital Controller IC for DC-DC Converters Operating at Switching Frequencies Beyond 10 MHz[ J] .IEEE Trans.Power Electron.22(5)：1693-1707.

[ 15] 程佩青.數字信號處理教程(第二版)[M].北京：清華大學出版社， 2004， 392-440.