風險的兩種度量方法
——信息熵與方差
趙秀菊
(襄樊學院 數學與計算機科學學院, 湖北 襄樊 441053)
風險的兩種度量方法
——信息熵與方差
趙秀菊
(襄樊學院 數學與計算機科學學院, 湖北 襄樊 441053)
信息熵和方差都被用作不確定性的度量,之間理應存在一定的科學關系. 從信息熵與方差的公式入手討論信息熵和方差在風險度量時的優缺點,指出之間的關系. 最后給出它們在一些領域的應用.
風險度量;信息熵;方差;概率分布
在Markowitz的均值—方差模型中,用方差度量風險;Massoumi and Racine[1]考慮到有時候我們并不能很好的了解金融市場的概率分布時,信息熵更適合度量不確定性;Mccauley[2]論述了信息熵可以反映股票市場的紊亂性和不確定性;Reesor. R,Ou. Jianshe[3]分別從相對熵、增加的熵的角度考慮了風險的度量.信息熵和方差都被用作不確定的度量,那它們之間有何關系呢?它們又有哪些應用呢?本文將對此作以討論.
1 信息熵和方差的基本定義
信息熵原本是熱力學中表征系統能量分布均勻程度或系統內部粒子無序程度的一個物理學基本概念,20世紀40年代信息論之父Shannon將其引入了信息論的范疇并取名為信息熵,用以度量信源的平均信息量. 他當時的思路是:能否定義一個量在某種意義上能度量作為這個過程所產生的信息是多少?或者信息速率是多少?他把信息量作為信息論的中心概念,在這樣思想指導下,用Markov過程的統計特性,即它的“熵”來表征信源的特性,給出下面的信息熵公式[4].
1.1 離散型分布的信息熵和方差
對于某個離散型隨機變量X,設X的分布律為{pi},其中(i = 1,2,,n),則信息熵作為風險變量X的風險度量為:
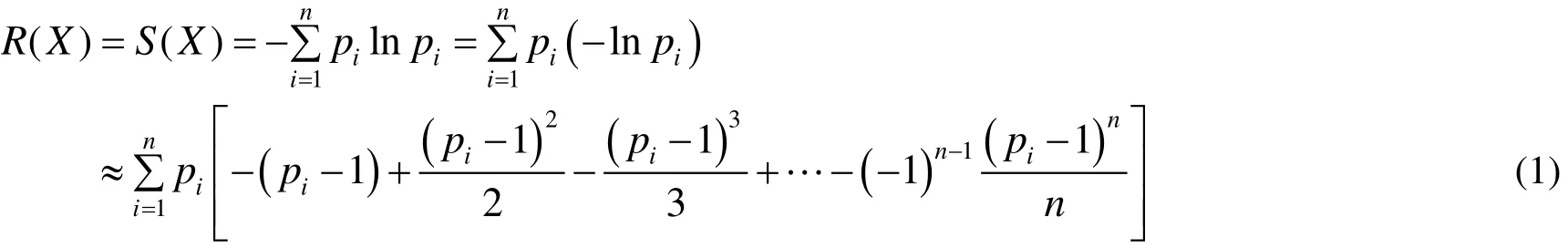
而方差作為風險變量X的風險度量R( X)為:
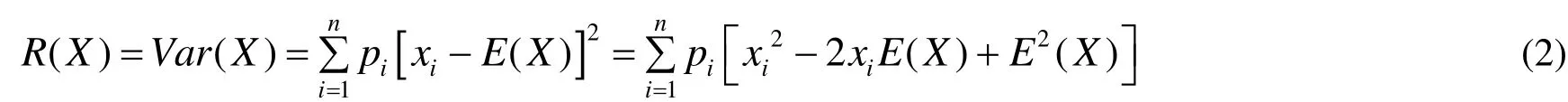
1.2 連續型分布的信息熵和方差
對于某個連續型隨機變量X,其概率密度函數為p( x),則該連續型隨機變量X的信息熵和方差分別為:

應用以上公式應注意以下幾點[5]:
1) Shannon認為信息是不確定性的減小或消除,即得到的信息越多,信源的不確定性就越小,所以信息熵是從平均意義上來表征信源總體信息的側度,是隨機變量不確定性程度的度量,其值越小,不確定性程度越小、隨機性越小,但這種度量是整體性的、平均的.
2) 信源的輸出是隨機的,即可以用概率分布來描述信源,這是信息論的一條假設.
3) 通過數學方法可以證明,當信源可能出現的各種狀態等概率時,此時信息熵最大,信源的平均不確定性最大,這一結論稱為最大熵原理.
2 信息熵與和方差的比較
早在20世紀50年代諾貝爾經濟學獎獲得者Markowitz就提出了用方差作為風險的度量,時至今日該方法仍得到了空前廣泛的應用.Luce通過考察風險行動的特定變換對于風險感知的影響,提出了風險度量的信息熵方法.下面對這兩種方法的異同總結如下:
1) 信息熵是對系統整體的一種度量,而且在已知矩約束的條件下可以推測出最“無偏”的概率分布;而方差反映了隨機變量的取值與其數學期望的偏離程度,是集中在隨機變量數學期望附近的度量.
2) 當且僅當一個隨機變量的概率為1時,其信息熵值為0;方差也是如此.
3) 對于相互獨立的狀態,其信息熵的和等于和的熵;方差也是如此.
4) 方差度量風險只適用于損失的概率分布為對稱的情況,當概率分布非對稱時,僅用方差來度量風險大小顯然是不夠的,還應該包括高階矩的信息,例如對小概率的極端事件對應的風險,只用方差度量風險顯然不夠;而信息熵度量方法對風險變量的分布沒有要求.
5) 方差只刻畫出風險變量的二階矩特征;而信息熵則可以表達風險變量的多階矩特征,能更好地描述風險的情況[6].
6) 方差是在已知統計數據序列下進行計算的,具有滯后性;而信息熵是對概率分布的一種無偏估計,因此是可以起到預測作用,信息熵的這一特性是目前眾多度量方法所不具備的.
7) 度量風險的信息熵和方差變大,說明風險變量的風險較大;反之亦然.
8) 方差不是單調函數,所以,當收益率高于期望收益率時,仍然要對方差函數進行懲罰,不符合投資者的心理狀況;而信息熵函數是單調的.
9) 在金融資產的風險度量方面,信息熵方法和方差法具有一致性[6].
10) 用方差來度量風險,需要進行方差協方差矩陣的計算,計算量相當復雜;而用信息熵來表示風險就不存在這種復雜的計算,計算方法相對簡單.
11) 信息熵的表達式中只含有P,所以只是計算風險變量X的概率分布;而方差的表達式中既含有變量X,又含有P,可以計算收益或損失,但方差表示的是正負兩種偏差.
12) 信息熵和方差都是P的連續函數.
13) 方差度量無法比較不同金融系統之間的不確定性;而信息熵度量方法使不同金融系統之間的比較成為可能,這也是現有度量方法鮮有的功能.
為了更好的了解信息熵和方差的直接關系,下面舉幾個特例,把信息熵寫成方差的函數.下面來討論狀態為連續型的隨機變量,對于一些特殊分布,兩者之間的關系.
1) 當狀態θ服從正態分布 N(μ, σ2),θ的密度函數為:
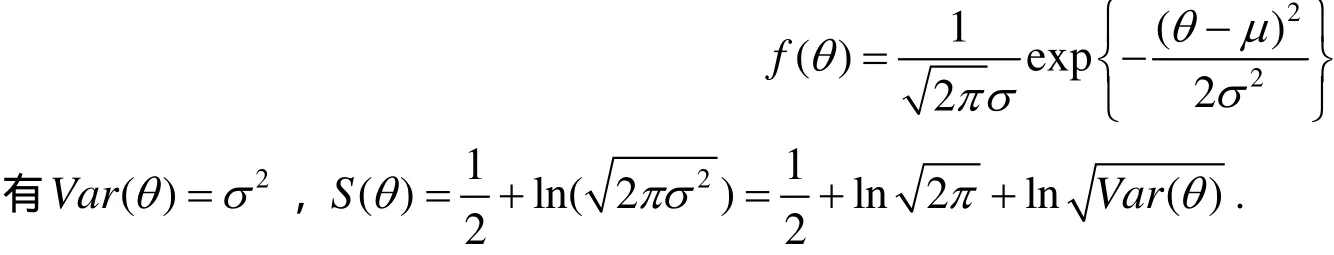
2) 當狀態θ服從以λ為參數的指數分布,密度函數為:
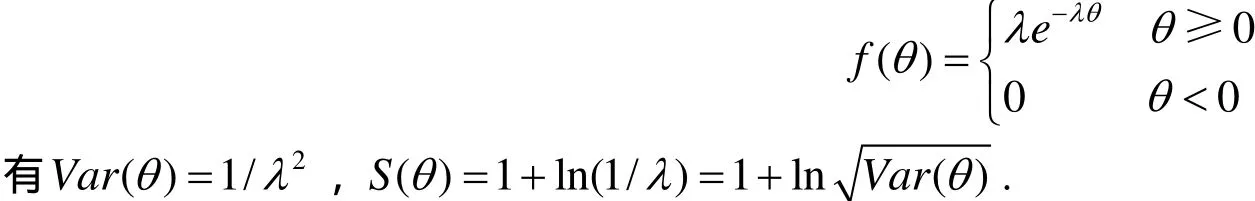
3) 當狀態θ服從U[ a, b]的均勻分布(a 可以看出,在上面三個分布中,信息熵是方差的單調遞增函數. 二者作為風險的度量進行決策行動排序是一致的. 但對于離散型隨機變量,信息熵與方差無關. 這個性質揭示出兩種常見的隨機變量之間的本質性差異. 3.1 在學校教學質量評價體系上的應用 當然可以利用方差來評價成績狀況,但是方差存在一定的片面性與局限性,為克服這方面的不足,可以用信息熵定義如下公式: 式中,A為分析對象的總分數,iθ為設定區域的總分數,n為區域的個數. 例如考察某科目的統考成績,A為各班成績的總和,iθ為各班成績,n為班級的個數. 實踐表明,若成績呈正態分布時,S值一般在1.5~1.7之間,當S<1.2時,成績的概率分布趨于集中,說明試卷的區分度小. 3.2 在股票投資中的應用 1) 李百吉,郭正權[6]選擇上證50指數50只樣本股作為研究樣本,進行數據處理,得到每個期望收益率所對應的信息熵和方差,在同一個圖中做出信息熵和方差關于期望收益率的變化趨勢圖,從圖可以看出,信息熵的變化趨勢和方差的變化趨勢基本上是一致的,而且信息熵曲線和方差曲線基本上是一種平行關系,這說明在度量股票風險方面,信息熵和方差方法是一致的. 2) 李英華[7]等給出了信息熵-標準差模型 其中:R( X)表示事件X的風險, SX(θ)為風險事件X在θ狀態的信息熵,0<λ≤1為常數,是決策者的風險偏好系數,王昕[8]將其用于股票投資中. 3.3 在證券投資組合中的應用 馬科維茨以證券收益率的方差作為投資風險的測度建立了組合證券投資的均值-方差模型,李華建立了均值-熵模型[9]: 其中: X = (x1, x2,,xn)T為投資比例向量;C表示證券收益率的方差協方差矩陣;E是投資者經過投資組合之后經過一個階段期望達到的收益. 李華[9]通過一個具體的實例利用兩個模型分別計算進行比較發現:所得結果是一致的. 3.4 在比例再保險中的應用 根據比例再保險的特點,Markowitz的均值-方差模型被應用于再保險問題的研究中,但是由上面討論知方差在度量風險時存在缺陷,我建立了均值-方差-熵優化模型: 其中: α= (α1,α2,,αn)T為自留額向量; L = (l1, l2,,ln)T為附加保費向量; V= [σij]n×n是向量X= (X1,X2,,Xn)T的協方差矩陣, X1,X2,,Xn是分出公司承保的n個險種,這里假定V是正定矩陣;e= (1,1,,1)T是一個所有分量均為1的向量;c表示分出公司的預期收益。那么保險公司分保后的問題是選取合適的自留比例向量α,使期望總收益最大和總風險最小.實證結果表明,采用均值-方差-熵優化模型所求的自留額分保后,能大大降低風險. 3.5 在保險定價中的應用 張闞[10]等定義的最大熵-均值方差保費原則為: 其中,P為保費,E( X)和Var( X)分別是基于最大熵分布的均值和方差,S是最大信息熵值,λ是一個大于零的常數. 在傳統均值方差保費原則基礎上了熵值附加項,建立了最大熵-均值方差保費原則,體現了保費制定的合理性,且易于求解. 隨著各學科的相互滲透和科學綜合化發展,熵概念已遠遠超出其最初的范疇. 目前,信息熵的概念在自然和社會科學的許多領域中得到廣泛的推廣和應用,信息熵已成為了一種新的世界觀. 本文討論了信息熵和方差在度量不確定性方面的異同,將他們的優缺點進行了詳細的歸類,還列舉了他們在其它領域的一些應用. 為風險度量的研究者提供了該方面的情況,并為進一步研究奠定了基礎. [1] MASSOUMI E, RACINE J. Entropy and predictability of stock market returns [J]. Journal of Econometrics, 2002, 107: 291-212. [2] MCCAULEY J. Thermodynamic analogies in economics and finance: on stability of markets [J]. Physica. A, 2003, 329: 199-212. [3] OU JIANSHE. Theory of portfolio and risk based on incremental entropy [J]. Journal of risk finance, 2005, 6(1): 31-39. [4] SHANNON C E. A mathematical theory of communication[J]. ACMSIGMOBILE Mobile Computing and Communication Review, 2001, 5(1): 3-55. [5] 孫 亮, 徐友全, 王德東, 等. 信息熵在設計風險管理中的應用研究[J]. 山東建筑大學學報, 2009, 24(6): 518-521. [6] 李百吉, 郭正權. 股票風險度量的熵方法和方差法的一致性的實證研究[J]. 金融經濟, 2005, 8: 70-71. [7] 李英華, 李興斯, 姜昱汐. 信息熵度量風險的探究[J]. 運籌與管理, 2007, 16(5): 111-116. [8] 王 昕. 信息熵風險函數在股票投資中的實證研究[J]. 北京機械工業學院學報, 2008, 23(3): 64-67. [9] 李 華, 李興斯. 證券投資組合理論的一種新模型及其應用[J]. 運籌與管理, 2003, 12(6): 83-86. [10] 張 闞, 豐 雪. 最大熵分布在投資組合中的應用研究[J]. 沈陽農業大學學報, 2007, 38(6): 881-884. (責任編輯:饒 超) Two Solutions to Risk Measurement: Information Entropy and Variance ZHAO Xiu-ju Both information entropy and variance are used for the measurement of uncertainty, there should be certain scientific relationship between these two. This paper discusses advantages and disadvantages in risk measurement by information entropy and variance from their calculation formulas. At last, their applications are offered. Risk measurement; Information entropy; Variance; Probability distribution O211.5 A 1009-2854(2010)02-0012-04 2009-12-20 趙秀菊(1980— ), 女, 湖北鐘祥人, 襄樊學院數學與計算機科學學院講師.
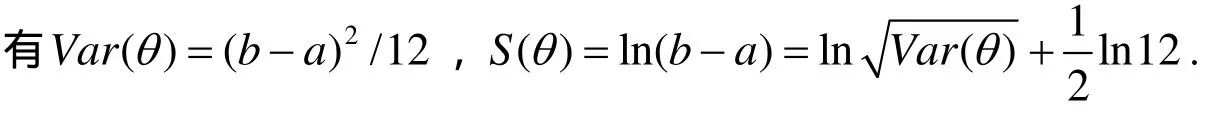
3 信息熵與方差的應用
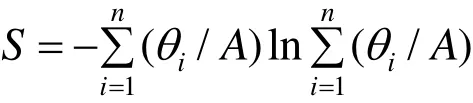
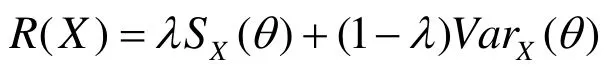
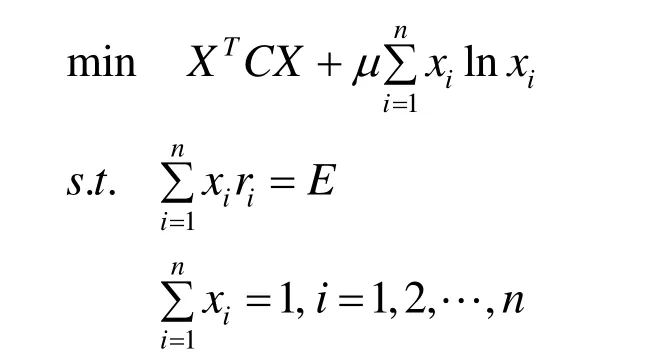
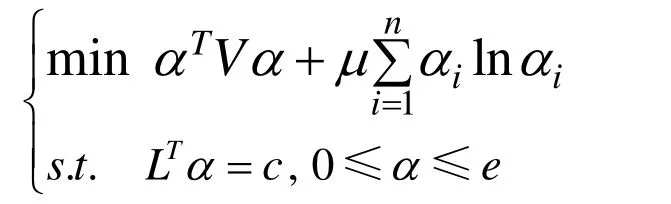

4 結語
(School of Mathematical & Computer Sciences, Xiangfan University, Xiangfan 441053, China)

