狀態預報值服從污染正態的抗差估計

莊常陵

(襄樊學院 數學與計算機學院, 湖北 襄樊 441053)

狀態預報值服從污染正態的抗差估計

莊常陵

(襄樊學院 數學與計算機學院, 湖北 襄樊 441053)

利用等價權原理，討論了狀態預報值服從污染正態分布的抗差估計，并利用影響函數，說明所給出的估計的確能減免粗差干擾，并針對估值的計算問題進行了討論.

抗差估計；污染正態分布；影響函數

離散時間狀態系統可以同時用狀態方程:

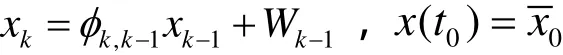
和觀測方程:

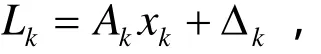
來描述. 假設狀態輸入噪聲{Wk}與觀測噪聲{Δk}均為期望為0的“白噪聲”序列，{Wk}、{Δk}和系統的初態互不相關，{Wk}、{Δk}均為服從正態分布的隨機序列. 則Kalman給出的最優估計x?k的遞推公式[1]:

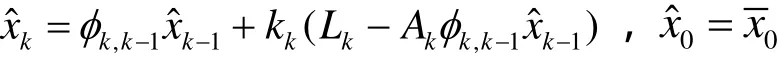
或

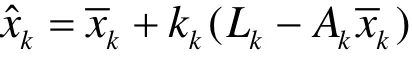
然而，實踐證明嚴格服從某一特定分布的觀測數據是不存在的. 如果狀態輸入噪聲向量和觀測噪聲中含異常噪聲而不服從正態分布，即狀態預報值和狀態觀測值Lk受到異常干擾時，Kalman給出的估值不但不是系統狀態的最優估值，甚至會偏離真值，造成難以預料的影響. 文獻[2]討論狀態觀測值Lk服從污染正態分布，但狀態預報值服從正態分布的抗差估計，下面將討論狀態觀測值Lk服從正態分布，但狀態預報值服從污染正態分布的抗差估計.

1 參數估計

狀態觀測值Lk服從正態分布，但狀態預報值服從污染正態分布，即

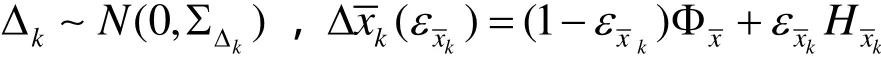
其中，Φx為標準正態分布，Hxk為干擾分布， εxk為污染率.

式中，kP為觀測值的權陣

式(1)求級值，并令 β′(?) =η(?)得

式(2)中， [η( δ x?k)]為列向量，其形式可選為常見的φ函數形式[1]. 取等價權元素為:

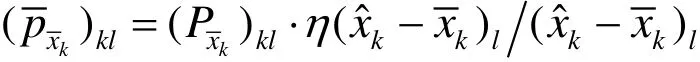
迭代解式為:

另一種解法是將準則(1)式改成:

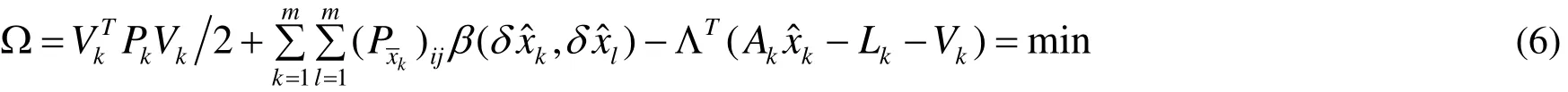
(6)式分別對Vk，求導并令為零，得:

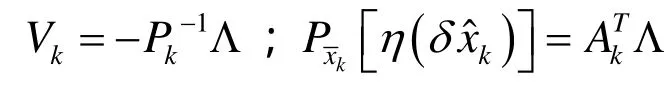
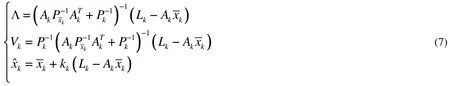
2 估值的抗差分析

將式(2)表示成泛函形式

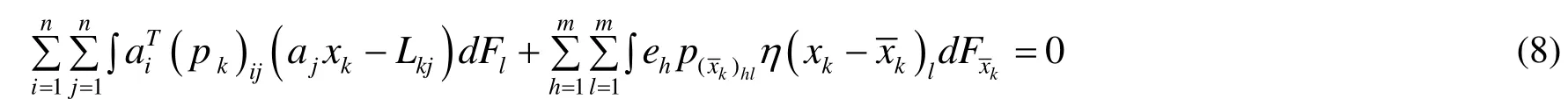
同理，觀測值Lkj對x?k的影響函數可寫為:

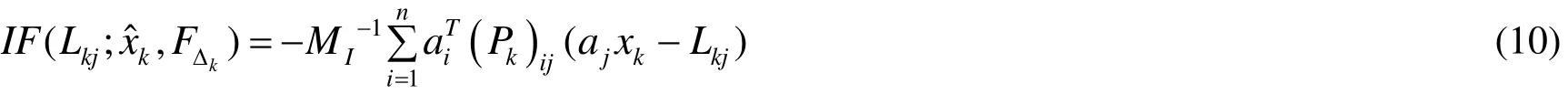
從Lkj對x?k的影響函數(10)式可以看出，因為假設觀測值Lk未受粗差污染，所以對觀測值未施加控制.

3 估值的驗后協方差陣

式(5)兩端同時減去參數的真值xk再乘以相應的轉置后取數學期望，得驗后協方差:

4 關于計算問題的討論

LS—M 估計的計算與一般估計相似，但計算時采用不同的解式其計算量和迭代收斂速度是不相同.一般情況下，當觀測值的個數少于狀態未知參數個數即nm時，可采用式(5)求估計值. 式(4)還可寫成:

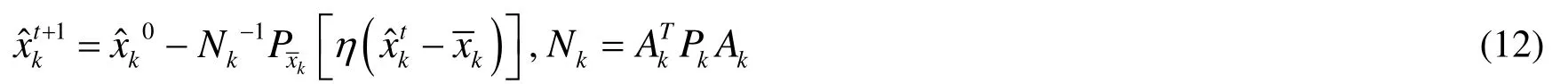
[1] 陳希孺, 趙林城. 線性模型中的M方法[M]. 上海: 上海科學技術出版社, 1996.

[2] 莊常陵. 觀測值服從污染正態分布的抗差估計[J]. 襄樊學院學報, 2008(2): 14-17.

[3] 莊常陵. 混合型正態分布的抗差最小二乘估計[J]. 襄樊學院學報, 2007(2): 5-8.

[4] 周江文, 黃幼才, 楊元喜, 等. 抗差最小二乘法[M]. 武漢: 華中理工大學出版社, 1997.

（責任編輯：饒 超）

Robust Filtering Whose Status Prediction Value Obeys Polluted Normal Distribution

ZHUANG Chang-ling
(School of Mathematical & Computer Sciences, Xiangfan University, Xiangfan 441053, China)

With equivalent weight principle, the robust filtering whose status prediction value obeys polluted normal distribution is discussed. With the help of influence function, it holds that the filter given can indeed derate disturbance of gross error. At last, the calculating issues of estimate value are also discussed.

Robust filtering; Polluted normal distribution; Influence function

O21

A

1009-2854(2010)02-0005-03

2009-12-29

湖北省教育廳科研項目(B200725002)

莊常陵(1968— ), 女, 江蘇常州人, 襄樊學院數學與計算機學院副教授.