海森伯格XY模型的負值度

劉思平

(襄樊學院 物理與電子工程學院, 湖北 襄樊 441053)

海森伯格XY模型的負值度

劉思平

(襄樊學院 物理與電子工程學院, 湖北 襄樊 441053)

利用一種通用量子糾纏度——負值度(Negativity)，研究熱平衡時在外加磁場(沿z軸)下兩量子比特海森伯格XY模型的熱糾纏. 當各向異性系數γ足夠大時，出現糾纏復蘇現象，而且對于一有限溫度，可以調節外加磁場來產生糾纏. 而對各向同性，當溫度比臨界溫度高時，負值度為零，與外加磁場無關.

量子糾纏；海森伯格模型；負值度；熱糾纏；

量子糾纏現象是量子理論最重要的特性之一，是能夠實現經典信息不可能實現的新功能的源泉. 量子信息學直接推動了糾纏態理論的發展. 糾纏態在量子態傳輸[1]、密鑰分配[2]等方面都起著關鍵的作用. 對糾纏定量的描述即糾纏態的度量是一個復雜而困難的問題，也是量子信息理論中一個重要的課題. 現在關于兩粒子系統純態糾纏理論已經相當完善[3]. 為了度量兩體混合態的糾纏，文獻[4-5]提出了多種糾纏度，其中負值度(Negativity)[6]是一種好的糾纏度量，對兩體混合態可以很方便的計算其糾纏. 糾纏的潛在應用價值激勵著人們去研究和控制它，除溫度以外，外加磁場是控制糾纏的另一參數. 在熱平衡下，由系統的哈密頓量H描述的態為ρ(T )= exp (? H/ k T)/Z ，其中 Z =Tr ??exp (? H/ kT )??為配分函數，k為玻爾茲曼常數. ρ( T)表示熱狀態，其糾纏即為熱糾纏[7]. 對兩量子比特各向同性的海森伯格模型在反鐵磁性情況下存在熱糾纏，但在鐵磁性情況下卻不存在熱糾纏[8]. 而對各向異性的海森伯格模型，其熱糾纏卻有不同，如XXZ模型的熱糾纏

[9]. 在本文中利用負值度(Negativity)計算了兩量子比特各向異性海森伯格 XY模型的熱糾纏，研究在熱平衡時溫度和外加磁場對糾纏的影響. 對各向同性，當溫度比臨界溫度高時，糾纏消失，與外加磁場無關.當各向異性系數足夠大時，發生糾纏復蘇現象，對一有限溫度，可以調節外加磁場來產生糾纏.

1 負值度(Negativity)

由Peres可分離判據[10]，對兩體低維2?2和2?3的系統，其部分轉置正定是判定是否為可分離態的充分必要條件，但對于其它情況這只是一個必要的條件. Vidal和Werner根據這一思想提出了一種通用的量子糾纏度量——負值度(Negativity)[6]，對兩量子比特來說，其定義為[11-12]：

其中，μmin為ρ的部分轉置的最小的本征值. 已經證明對兩量子比特可分離態其部分轉置只有一個負的本征值.對兩體糾纏，負值度可方便的計算其糾纏.

2 XY模型的負值度

兩量子比特各向異性Heisenberg XY模型在外加磁場B下(沿z軸)的哈密頓量為：

σi(i = x, y, z )為泡利算符，糾纏密度矩陣：Z為配分函數. J>0表示反鐵磁性情況，J<0表示鐵磁性情況.為簡單化，以下取k=1.

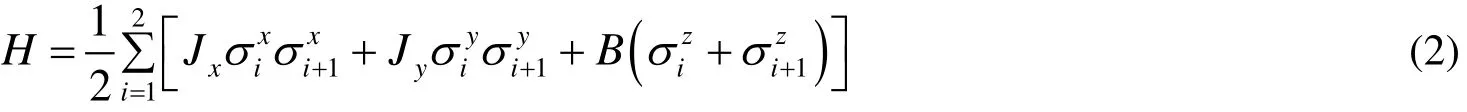
系統的本征態和本征值分別為：

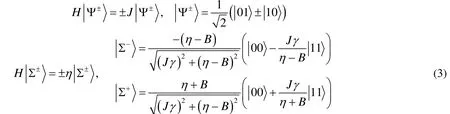
糾纏密度矩陣為:

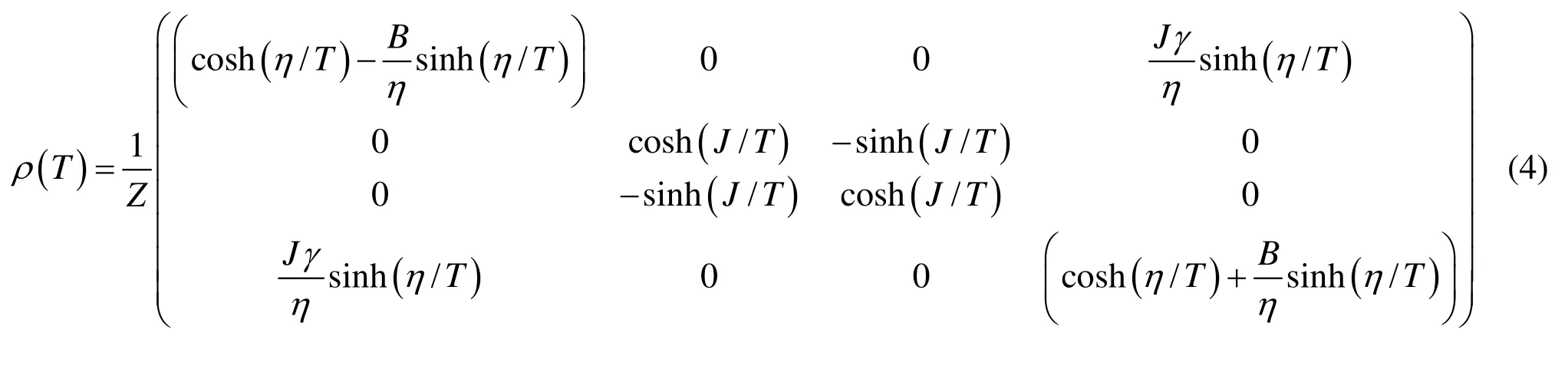
密度矩陣部分轉值的本征值為：

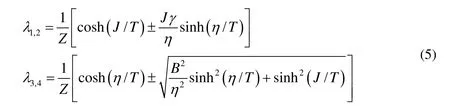
當各向異性系數 γ= 0,0.3,0.6時，利用式(1)畫出負值度與溫度和磁場的關系圖，如圖1和圖2. 由圖可以看出，它們有相似之處，當T=0和B=0時，負值度都為最大值，因為此時，系統為基態，即最大糾纏態Bell態.當γ=0各向同性時，如圖1所示，當T=0時，隨著磁場的增加，負值度保持一最大值不變即最大糾纏態，當B達到一臨界值BC時，負值度迅速減小到零，其中 BC=J=1.實際上，當B>J，基態是非糾纏態，在臨界點(T = 0,B = BC= J )發生了量子相變[13].

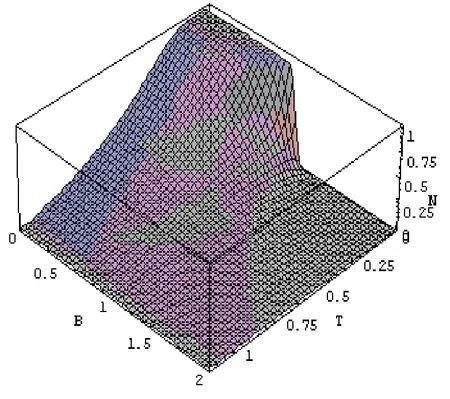
圖1 海森伯格XY模型的負值度與溫度和外加磁場的關系( J= 1,γ = 0)

對各向異性的情況，如圖2所示，當T=0時，隨著B的增加，起初負值度保持一定值等于其最大值，當B達到一臨界值BC時，負值度突然下降，這與各向同性的情況相似，所不同的是，當 B>BC時，負值度并不降為零，而且當γ足夠大時，負值度由最小值突然增加，經歷了一個糾纏復蘇過程，如圖2(b).

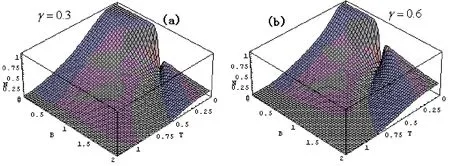
圖2 負值度與溫度和外加磁場的關系(J=1)

其實 B>BC時，當γ≥0.6都會發生糾纏的復蘇，如圖3畫出負值度與B的關系，對γ=0.3，當 B=BC，負值度急劇下降，當 B>BC，值值度單調下降.對γ≥0.6，當 B=BC，負值度急劇下降但并不降為零，當B>BC，負值度出現了復蘇，對γ=0.8同樣如此.

從密度矩陣可以看出，當ηJ時，系統的基態為仍為糾纏態，當具有相同的能量，都等于系統的最低能量.一般情況下，當T=0時，系統可表示為態的混合態，其密算符為，對，且當η=J時，，此時有即溫度T=0時，量子相變發生在系統為等概率混合的時候.

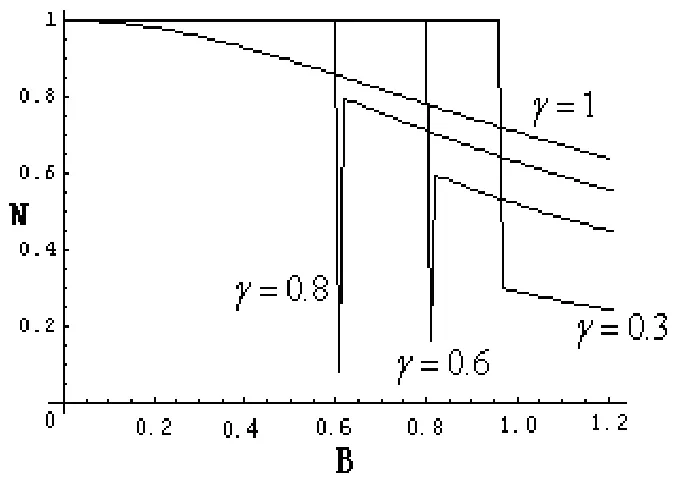
圖3 T=0時負值度N與磁場B的關系(J=1)

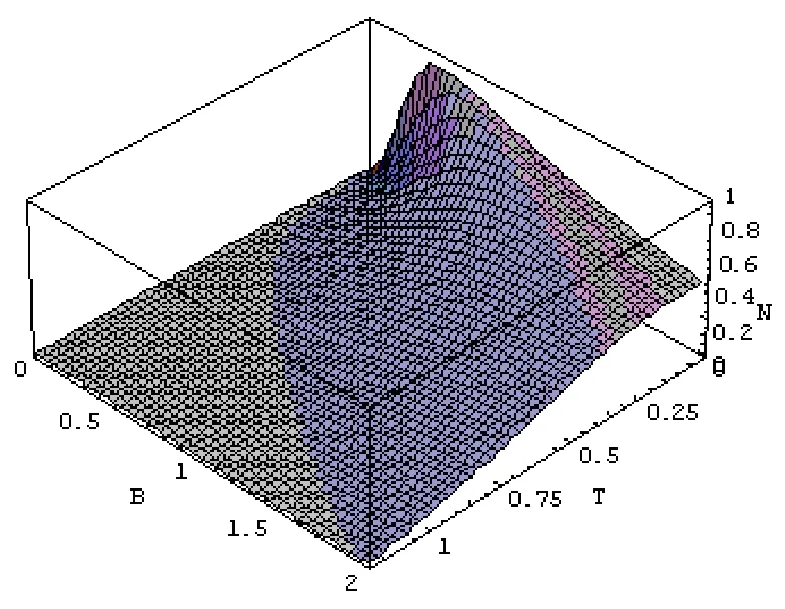
圖4 Ising模型的負值度( J= 1,γ = 1)

對Ising模型，即γ=1時，如圖4所示，當B=0時，系統負值度為零，即負值度僅由外加磁場決定.由圖3可以看出，當T=0時，隨著系數γ的增加，量子相變發生點不斷減小，當因為對Ising系統，當 B= 0,T = 0時，系統的態為Bell態的等概率混合，其糾纏為零.

3 結語

兩量子比特海森伯格XY模型的熱糾纏與各向異性系數γ、磁場B和溫度T有關. 對各向同性，當溫度高于臨界溫度高，系統沒有糾纏，與外加磁場無關，當γ足夠大時，存在糾纏復蘇現象，而且對于一有限溫度，可以調節外加磁場來產生糾纏.

[1] BENNETT C H, BRASSARD G, CREPEAU C, et al. Teleporting an unknown quantum state via dual classical and Einstein-Podolky-Rosen channels[J]. Phys. Rev. Lett., 1993, 70(13): 1895-1899.

[2] DEUTSCH D, EKERT A, JOZSA R, et al. Quantum privacy amplification and the security of quantum cryptography over noisy channels[J. Phys. Rev. Lett., 1996, 77(13): 2818-2821.

[3] 曾謹言, 裴壽鏞, 龍桂魯. 量子力學新進展:第二輯[M]. 北京: 北京大學出版社, 2001: 281.

[4] SCOTT HILL, WOOTTERS WILLIAM K. Entanglement of a pair of quantum bits[J]. Phys. Rev. Lett., 1997, 78: 5022-5025 .

[5] VEDRAL V, PLENIO M B, RIPPIN M A , et al. Quantifying entanglement[J]. Phys. Rev. Lett., 1997, 78: 2275-2279.

[6] VIDAL G, WERNER R F. A computable measure of entanglement[J]. Phys.Rev.A., 2002, 65:032314-032317.

[7] ARNESEN M C, BOSE S, VEDRAL V. Natural Thermal and magnetic Entanglement in 1D Heisenberg Model[J]. Phys. Rev. Lett., 2001, 87: 017901-017904.

[8] 劉思平. 海森伯格XXZ模型的熱糾纏[J]. 江漢大學學報: 自然科學版, 2009(3): 33-35.

[9] WANG XIAOGUANG. Effects of anisotropy on thermal entanglement[J]. Physics Letters A, 2001, 281(3): 101-104.

[10] PERES A. Separability criterion for density matrices[J]. Phys.Rev. Lett., 1996, 77: 1413-1415.

[11] ZYCZKOWSKI K, HORODECKI P, SANPERA A, et al. On the volume of the set of mixed entangled states[J]. Phys. Rev. A, 1998, 58: 883-892.

[12] EISERT J, PLENIO M B. A comparison of entanglement measures[J]. J. Mod. Opt., 1999, 46: 145-154.

[13] SACHDEV S. Quantum Phase Transitions[M]. Cambridge: Cambridge University Press, 1999.

（責任編輯：饒 超）

Negativity of Heisenberg XY Model

LIU Si-ping
(Physics and Electronics Information Technology Department, Xiangfan University, Xiangfan 441053, China)

Using a universal entanglement measure, negativity，we investigate the thermal entanglement of two-qubit Heisenberg XY model in thermal equilibrium at temperature T in the presence of an external magnetic field B. When anisotropy parameter γis large enough there occurs a revival of the entanglement. By adjusting the magnetic field B，one can produce entanglement for any finite T. For isotropic case there is no entanglement above a critical temperature that is independent of the external B field.

Entanglement; Heisenberg model; Negativity; Thermal entanglement

O431

A

1009-2854(2010)02-0008-04

2010-01-04

湖北省教育廳科學技術研究計劃優秀中青年人才項目(Q20082503)

劉思平(1975— ), 女, 重慶榮昌人, 襄樊學院物理與電子工程學院講師.