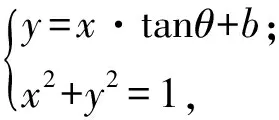一道應用題的變式教學及反思
● (通州高級中學 江蘇通州 226300)
教與學如同教學質量的2只翅膀,只有師與生雙翅有力,教與學兩翼互動,才能使教學質量飛揚.在解題教學中必須教與學并重,教與學有機結合.反思教學,既要強化教師教的反思,又要關注學生學的反思.這樣既能磨礪教師的教學本領,又能錘煉學生的學習能力.下面就一道試題的變式教學談談教與學的雙重反思,希望能帶給讀者一點啟示.
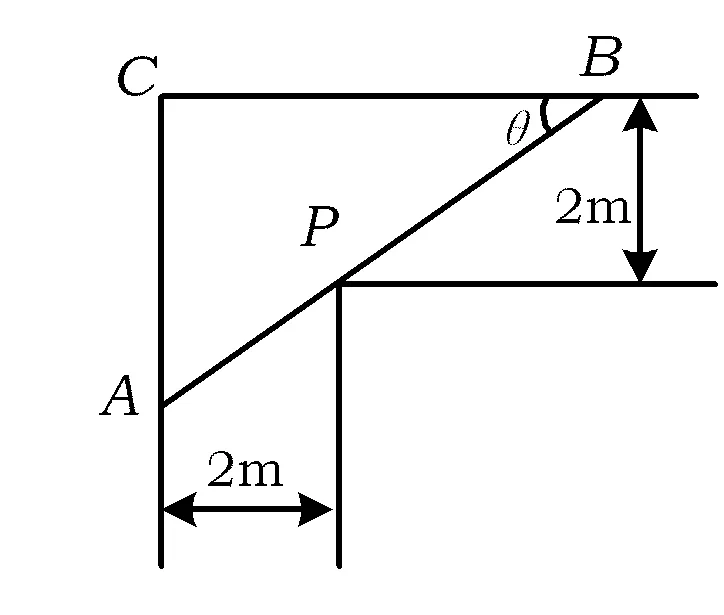
圖1
1 呈現典例
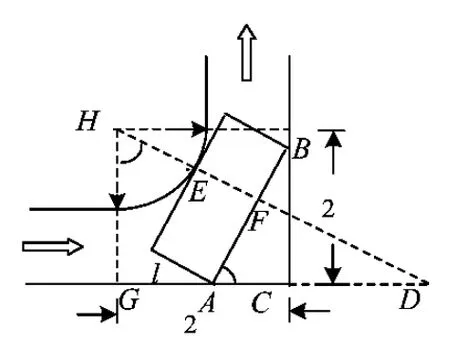
例1走廊的示意圖如圖1所示,其2邊走廊的寬度均為2 m.
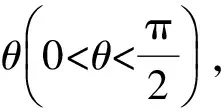
(2)一根長度為5 m的鐵棒能否水平(鐵棒與地面平行)通過該直角走廊?請說明理由(鐵棒的粗細忽略不計).
分析這是江蘇省南京市2009年高三期末調研測試題中的一道考題,是一道三角函數模型的應用題.第(1)小題需過建模關,第(2)小題需過閱讀分析關和運算關.
解(1)由題意得
(2)方法1通分得
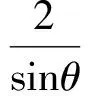
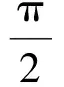
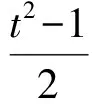
于是



因此
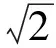
故鐵棒能水平通過該直角走廊.
方法2求導得

方法3平方得


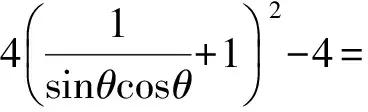
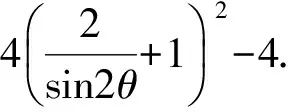
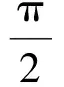
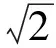
故鐵棒能水平通過該直角走廊.

0 于是 故鐵棒能水平通過該直角走廊. 于是 從而 故鐵棒能水平通過該直角走廊. 反思(1)解題關鍵點. 本題的建模過程應該不是很難,而運算應充分抓住原等式的結構特征,認真分析其結構的變化形式,靈活應變,多方位思考,然后使用不同的求解策略加以應對.通過這樣的反思,讓學生學會如何選擇思維的起點,開拓思路,積累破題的經驗和規律,培養思維的廣闊性. (2)解題技巧(運算技巧). 策略1利用三角關系式(sinθ+cosθ)2=1+2sinθ·cosθ,通過換元法來實施轉化,最終化為函數問題處理. 策略2直接利用導函數法求解. 策略3轉化成二次函數問題求解. 策略4直接利用基本不等式求解. 很多數學試題有多種解法,解題后要從多角度思考是否還有其他解法,通過尋找新的方法可以開拓思路,防止思維定勢,及時總結出各類解題技巧,養成“從優、從快”的解題思維方式,從而使思維更具有創造性. (3)解題易錯點. 在本題的建模過程中應注意實際問題的定義域,而第(2)小題中應注意到l越小越好,因此求的是l的最小值,運算中應注意θ的取值范圍和基本不等式中等號成立的條件. 變式1直角走廊的示意圖(如圖2所示),其2邊走廊的寬度均為1 m.現有一平板車,其平板面為矩形,它的長為2 m,寬為l m. (1)若平板車卡在走廊內,且∠CAB=θ,試求平板面的寬; (2)若平板車能順利通過走廊,其寬度不能超過多少米? 解(1)轉化為例1,如圖3,可知 MN=MD+DN=ME+EF+FN, 于是 得 圖2 圖3 變式2如圖4,一走廊拐彎處外側是直角形,內側是半徑為1 m的圓弧,走廊直道部分的寬均為1 m.現有一平板車,其平板面為矩形,它的長為2 m,寬為lm. (1)若平板車卡在走廊內,且∠CAB=θ,試求平板面的寬; (2)若平板車能順利通過走廊,其寬度不能超過多少米? 圖4 圖5 解法1(1)設H為圓弧的圓心,E為平板面的一邊與圓弧的切點,連結HE,并延長交AB于點F,交AC延長線于點D.因為 所以 AD=GD-GA=GD-(2-AC)= 2tanθ-2+2cosθ. 又 HD=HE+EF+FD=1+l+AD·sinθ, 所以 即 (2)令sinθ+cosθ=t,則 從而 圖6 解法2(1)由圓弧聯想到圓,即可建立直角坐標系,解決圓與直線的位置關系問題.如圖6,平板面的一邊與圓弧相切的直線為GH,則直線GH對應的方程為y=x·tanθ+b,圓O:x2+y2=1,得H(2,2tanθ+b).因為 HC=BC+BH, 所以 聯立 得 從而 (2)同解法1. 反思(1)解題關鍵點:能運用恰當的數學方法去建立解決數學模型,應該自己去領會、體驗,只有這樣才能將所學知識轉化為解決問題的能力. (2)解題技巧(建模技巧). 策略1從平面幾何的角度去建立和發現函數模型. 策略2從解析幾何的角度去建立和發現函數模型. (3)解題易錯點. 一道簡單的例題通過一系列的變式,合理控制和深化難度,可為訓練思維、深化認知、優化認知提供契機,這是培養解題能力、抽象概念能力的重要手段.通過變式教學,將知識串珠成線,從例題的典型性和規律性出發提高例題的“品味”,真正發揮經典例題、習題的多種功能;通過變式教學,不僅能使學生的思維始終處于極度興奮的狀態,思維得到升華,而且這也是課堂上開展研究型學習切實、有效的途徑.通過解題后的反思不僅能對知識的形成發展過程、解題思維過程有一個更清楚的認識,還有利于知識的深化、思維的縝密及高效課堂的形成.
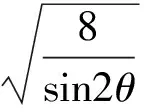

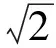

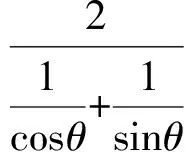
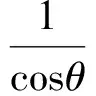
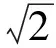
2 變式引申