一個不等式的推廣和完善

● (學軍中學 浙江杭州 310012)

《數學通報》2009年第12期數學問題解答中刊登的第1 824號問題是：

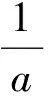
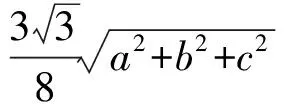
筆者根據供題人給出的解法對上述不等式進行了推廣，并給出了上面右邊式子的一個下界.

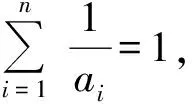
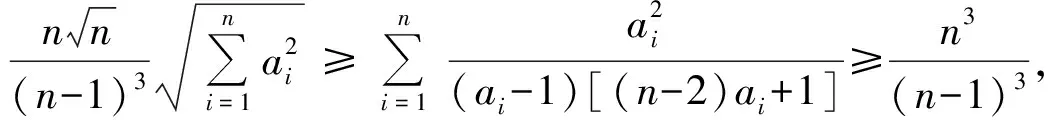
并當a1=a2=…=an=n時，取到等號.

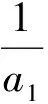
因為

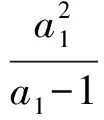
所以

故當n=2時，原不等式成立.

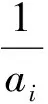
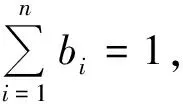
(1)先證明左邊的不等式.由柯西不等式可得

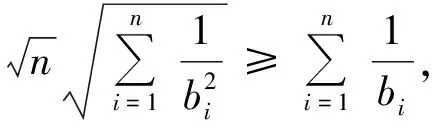
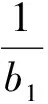
將上述n個式子相加可得

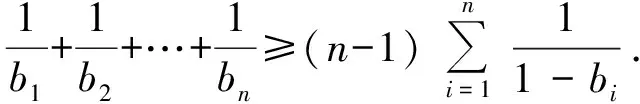
(1)

又由柯西不等式知

表5顯示，隨著青貯發酵時間的延長，5種不同比例混合青貯過程中大腸桿菌的數量大體呈先增加后逐漸減少的趨勢，直至最后檢測不出大腸桿菌的數量。0%、25%的青貯飼料中大腸桿菌數量在青貯發酵的第11 d左右達到高峰，為109數量級，50%的青貯飼料中大腸桿菌數量在青貯發酵的第20 d達到高峰，為109數量級。100%的青貯飼料中大腸桿菌數量在青貯發酵的第5 d左右達到高峰，為108數量級，到第45 d之后檢測不出大腸桿菌的存在。

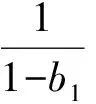
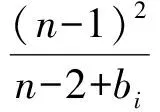
將上述n個式子相加可得到

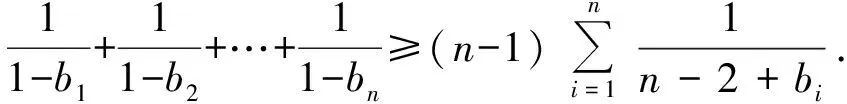
(2)

于是由式(1),式(2)可得

故

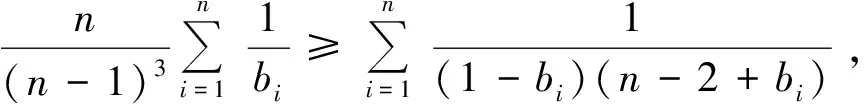
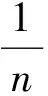
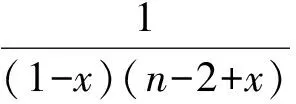
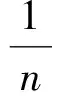
接下來證明:

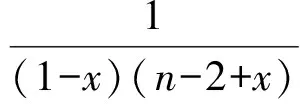
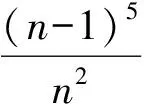
即

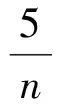
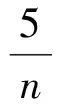
f′(x)=(nx-1)[(3n-6)x+2n-8x+9]，

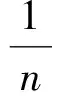
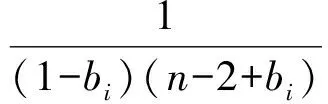
即

故

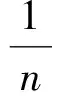
由(1),(2)可知,當n>2時，原不等式成立.