用代換法求無理函數的值域
2010-11-23 01:52:45常福一區90幢302室江蘇常熟215500
中學教研(數學) 2010年6期
● (常福一區90幢302室 江蘇常熟 215500)
用代換法求無理函數的值域
●周華生(常福一區90幢302室 江蘇常熟 215500)
用代換法求無理函數的值域,方法簡便、靈活,是一種很有用的解題方法.本文就4種常見的無理函數求值域問題從整體上分析一些解法和技巧,可供參考.為計算方便,本文使用以下3個公式(也可用判別式求):
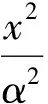
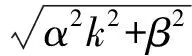

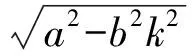
1 求y=+(a>0,c<0)的值域
當a,c同號時,用增減性解很方便.
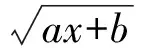
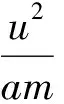
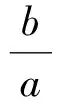
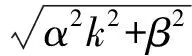
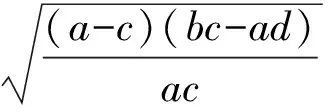
y的最小值可視具體情況通過所在的點來計算.
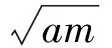
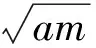
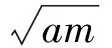
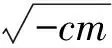
2 求y=-(a>0,c>0)的值域
當a,c異號時,可用增減性很方便地求解.
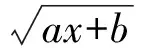

(1)
或
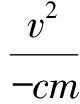
(2)
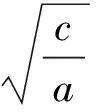

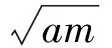
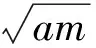
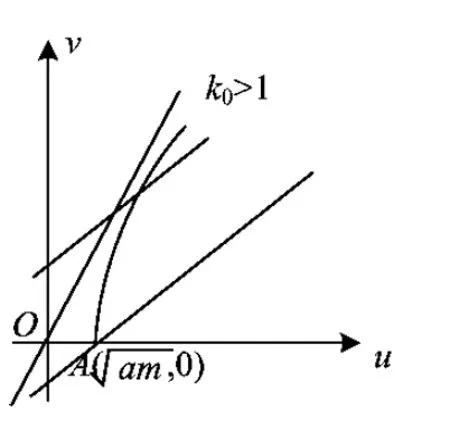
圖1
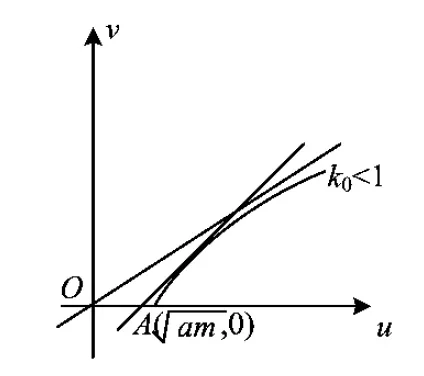
圖2
②當c 即 ②當c>a時,k0>1,如圖4.可按切線確定截距最小值,于是 即 圖3 圖4 或 流動資金暫按年運行費的10%計。流動資金從項目正常運行期的第1年初投入,隨項目運行,計算期末一次回收[3]。 (4) (1)當a>1,b>0時,如圖5,k0<1.由雙曲線方程(3),且切線確定截距最大值,得 即 圖5 圖6 即 即 圖7 圖8 (4)當0 從而 即 為避免復雜的討論,下面用實例來說明解題的方法. 解原方程可化為 其定義域由-2x2+13x-18≥0確定,即 即 即 解得 圖9 圖10 圖11 時,截距-s取最小值,此時 即 最后指出,本文前3個部分介紹的是一般的解題方法.對于具體問題,可按照所提方法直接求解,這比代公式方便許多.
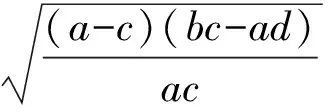

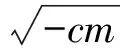

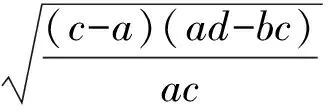
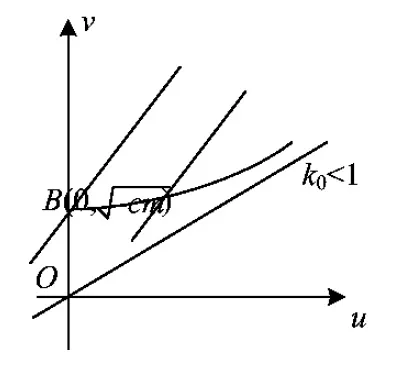

3 求y=-x(a>0,x≥0)的值域

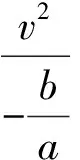
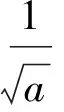

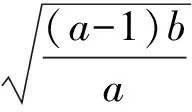
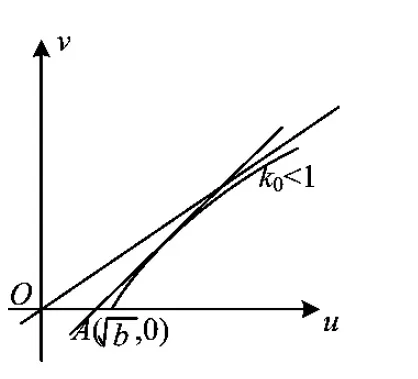

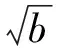
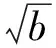
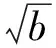
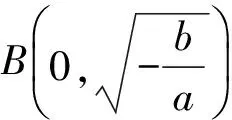


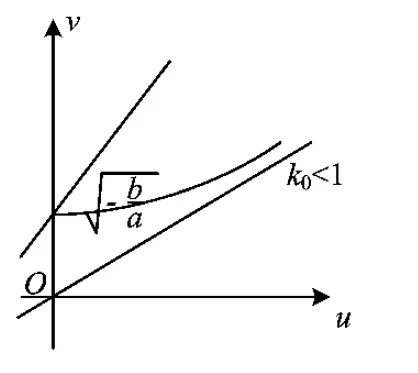
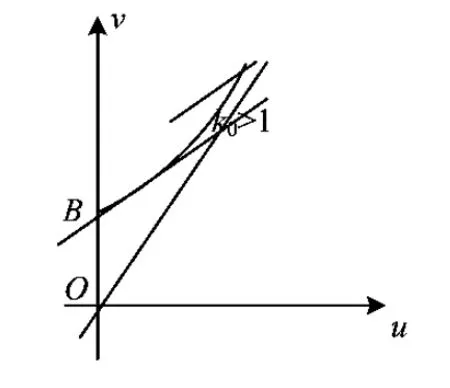
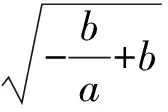
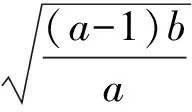
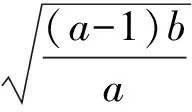
4 求y=kx+t+的值域
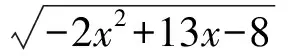
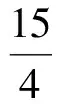
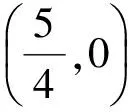

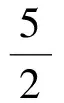
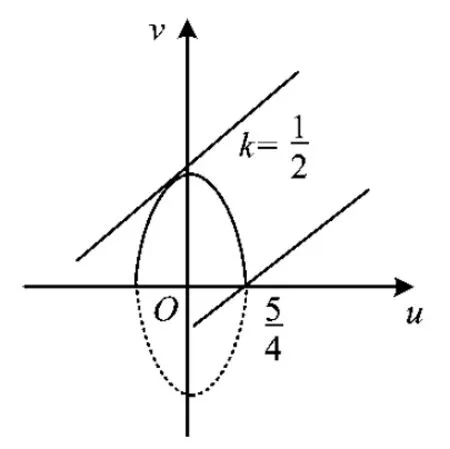
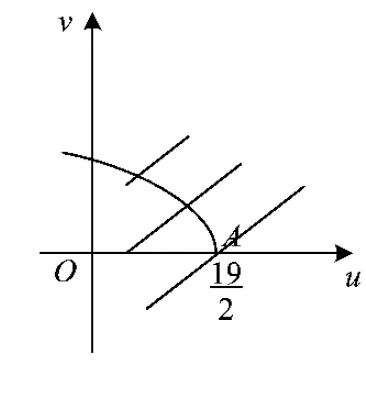
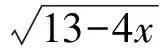
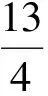




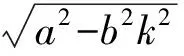
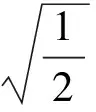
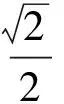
猜你喜歡
小學生學習指導(低年級)(2022年9期)2022-10-08 03:12:02
中學生數理化·中考版(2022年8期)2022-06-14 06:55:52
小學生學習指導(低年級)(2021年4期)2021-07-21 01:59:26
經濟技術協作信息(2018年11期)2019-01-14 03:07:16
中學生數理化·八年級數學人教版(2016年3期)2016-04-13 09:17:06
Coco薇(2016年2期)2016-03-22 02:42:52
Coco薇(2015年1期)2015-08-13 02:47:34
環球市場信息導報(2015年18期)2015-06-21 01:17:40
小雪花·成長指南(2015年4期)2015-05-19 14:47:56
溫州職業技術學院學報(2013年1期)2013-03-20 15:33:08

