四面體中的Cordon不等式

● (沙坡頭區宣和鎮洪學校 夏中衛 755006)

四面體中的Cordon不等式

●張寧(沙坡頭區宣和鎮張洪學校 寧夏中衛 755006)

1967年,V.O.Cordon建立了涉及三角形高與邊長之間的如下不等式[1]:

本文將三角形類比到四面體，得到下述定理.

定理1設四面體A1A2A3A4的側面面積分別為S1,S2,S3,S4，相應面上的高分別為h1,h2,h3,h4，外接球和內切球半徑分別為R,r,則

當且僅當四面體為正四面體A1A2A3A4時,等號成立.

定理的證明需要用到以下2個引理.

引理1[2]在四面體A1A2A3A4中，

引理2設四面體A1A2A3A4的體積為V，則

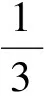
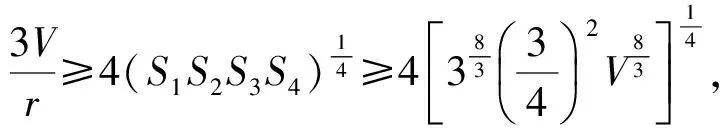
即

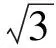
由文獻[3],可知

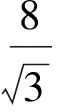
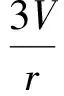
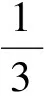
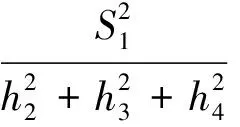
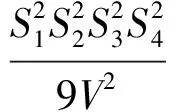
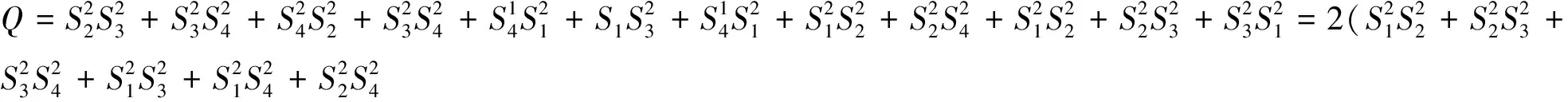
從而由式(4)及式(5),可得

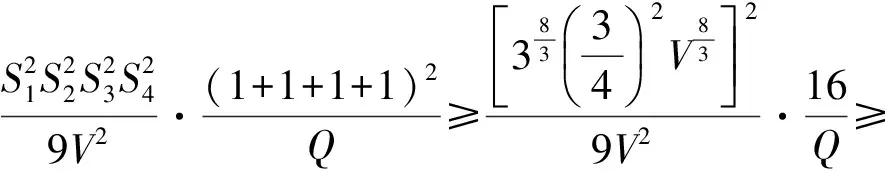
當四面體A1A2A3A4為正四面體時，R=3r.

由此可得如下推論1.

推論1在正四面體中，

定理2設四面體A1A2A3A4的側面面積分別為S1,S2,S3,S4，相應面上的高分別為h1,h2,h3,h4，外接球和內切球半徑分別為R,r,則

其中∏表示循環積.當且僅當四面體A1A2A3A4為正四面體時,等號成立.

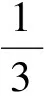
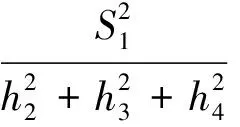
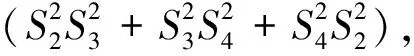
由定理1的證明可知

(8)

因此

結合引理1知

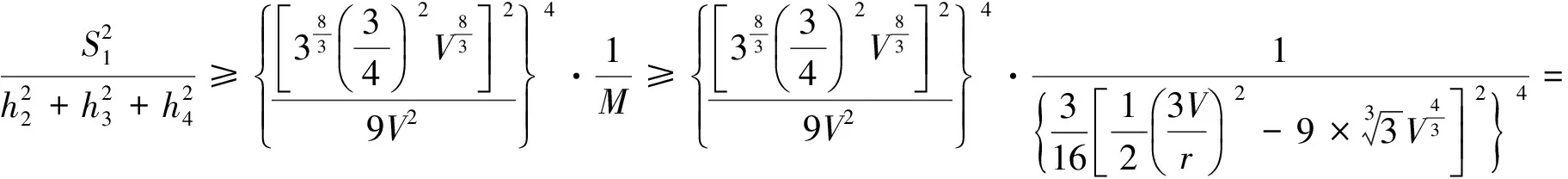
結合引理2易得

定理證畢.

當四面體A1A2A3A4為正四面體時，R=3r.

由此可得如下推論2.

推論2設正四面體A1A2A3A4的四面面積分別為S1,S2,S3,S4，相應面上的高分別為h1,h2,h3,h4，外接球半徑為R,則

[1] 匡繼昌.常用不等式[M].3版.濟南：山東科學技術出版社，2004:220.

[2] 楊路.來自四面體的挑戰[J].中學生數學,1987(1)：28.

[3] 孔令恩.三角形到四面體的又一個等價變換[J].數學通訊,1996(9):32-34.

[4] 陳計，王振.Neubery-Pedoe不等式的四面體推廣[J].數學通訊,1994(2)：22.