橫向受載空心樁動力性能研究

張永謀，楊 敏

（1.蘭州交通大學土木工程學院，甘肅蘭州730070；2.同濟大學地下建筑與工程系，上海200092）

0 引言

我國采用的計算推力樁的現行方法，如張有齡法、m法、c法等，都是單一參數法[1～4]，即在冪函數土抗力模數K=mxq中，q預先確定，只有一個待定參數m值的方法。用單一參數法計算推力樁，有一個共同的缺點，即樁在地面處的撓度、轉角、樁身最大彎矩及其所在的位置等，不能同時很好地符合實測值，只能湊合到較為接近的程度。其原因是待定參數的數目不夠，或選擇得不恰當所致。但是，對樁基礎的設計至關重要，是值得十分重視的問題。解決問題的途徑之一是增加參數，并且要求參數選擇得恰當。綜合剛度原理和雙參數法，用于推力樁的非線性分析和動響應分析，能取得比較滿意的效果。

1 無量綱差分方程式的推導

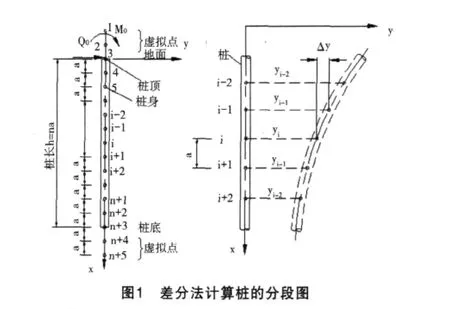
將樁身劃分為n個單元，則共有n+1個劃分點。要這n+1個點上都能建立差分方程式，則在樁軸兩端延伸線上分別設兩個點[5,8]。因此，最后得到樁身劃分點的編號如圖1所示。

現在，樁身的劃分點為n+1個，再加上樁頂以上和樁底以下各兩個虛擬點，則共有n+5個未知側移需要求解，但只有n+1個方程，所以需要根據樁底和樁頂處的邊界條件得出另外四個附加方程，連同上述n+1個方程，剛好聯立求解這n+5個點側移值。

根據有限差分法，得到樁身各節點位移函數：

式（2）即為樁身位移的遞推公式，它可用于樁身第i=3，4，…，n+3等點，得到n+1個方程，再加上4個邊界條件，共計n+5個方程，解這組n+5元聯立方程，就可以得出包括虛擬點在內的n+5個節點的位移yi，進而可以通過各階中心差分式求出各個節點的轉角和內力。

2 試驗樁實例計算

一樁基水平激振試驗如圖2所示，實驗在砂坑中進行，樁為150 cm長的鋼管，土礫砂，承臺為鋼筋混凝土，樁、土、承臺的基本資料見表1所列。

共振時頻率f=9.4 Hz，

地面處水平位移的模為|y0|=0.068 08 cm，

轉角的模為|φ0|=0.002 36 rad，

彎矩的模為|M0|=5.88 kN·cm，

表1 樁、土、承臺基本資料匯總表

剪力的模為|Q0|=0.347 kN。

用前述方法，取1/n=0.75，α=0.043 63 cm-1，綜合剛度EI=2.0202×108N·cm2時，

令Ωy=0，則從式(84)就得到車輪不旋轉時環向指數為m的固有頻率和振型。車輪旋轉時，有離心效應(由離心矩陣Mc描述)和陀螺效應(由陀螺矩陣G描述)，它們(尤其是陀螺矩陣G)的存在使得不旋轉車輪的一個固有頻率變成旋轉車輪的2個特征頻率。

2.1 系數計算

代入已知參數可求得各方程的系數。

2.2 列方程計算撓度

用遞推公式：

yi+2-4yi+1+ （6+ Ai）yi-4yi-1+yi-2=0可寫出16個方程。

用地面處樁頭邊界條件可寫出兩個方程，即：

用樁底邊界條件可寫出兩個方程，即：

聯立解線性方程組。

方程形式如：

AY=B

其中：用克拉默法則解此線性方程組，可解得撓度yi，用于后續計算。

2.3 轉角計算

2.4 彎矩計算

2.5 剪力計算

2.6 土抗力集度計算

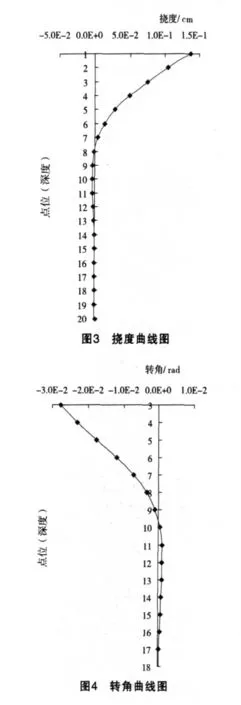
2.7 計算結果（見圖3～7）

3 實心樁與空心樁的對比

地質條件：0～14 m，中砂、中密、飽和；14～17 m，粗砂、中密、飽和；17～21 m，砂質粘土、密實、半堅硬。

荷載及比值：樁在地面處所受的動力矩幅值M0和橫向動力幅值Q0之比e=M0/Q0=0.25 m，其中Q0=60×104N。

表2 樁身彎矩與撓度的實測值和計算值匯總表

計算條件：1/n=0.5，m1=4.347 726 6 N·cm-3.5。

樁的物理幾何特征：

樁1：鉆孔灌注混凝土實心樁，樁徑D=1.62 m，樁的入土長度h=18.8 m，混凝土密度ρ=2.4×10-3kg/cm3，混凝土彈性模量Ep=3.0×106N/cm2，有鋼筋骨架。

樁2：鉆孔灌注混凝土空心樁，樁外徑D=1.62 m，樁內徑d=1.02 m，樁的入土長度h=18.8 m，混凝土密度ρ=2.4×10-3kg/cm3，混凝土彈性模量Ep=3.0×106N/cm2，有鋼筋骨架。

樁3：鉆孔灌注混凝土空心樁，樁外徑D=2.22 m，樁內徑d=1.52 m，樁的入土長度h=18.8 m，混凝土密度ρ=2.4×10-3kg/cm3，混凝土彈性模量Ep=3.0×106N/cm2，有鋼筋骨架。即，樁1樁身截面面積與樁3樁身截面面積相等，樁1實心樁面積為：2.060 15 m2，樁3空心樁面積為：2.055 13 m2。如圖8所示，樁1和樁3陰影部分面積相等。

計算參數見表3所列。

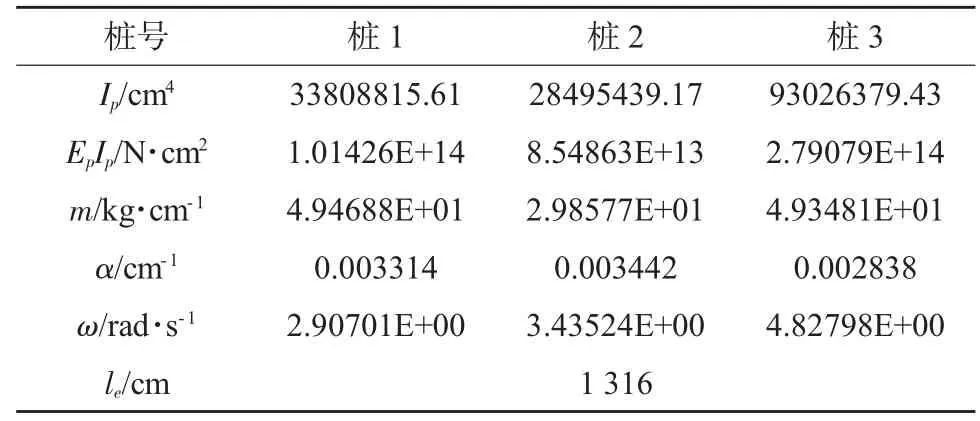
表3 計算參數表

圖9～13列出了樁1、樁2和樁3的撓度、轉角、彎矩、剪力和土抗力的對比曲線。

4 結論

該設計使用了等效懸臂法估算推力樁的固有頻率，之后，采用吳恒立提出的綜合剛度原理和雙參數法，計算共振時樁在地面處的撓度和轉角幅值，以及樁身最大彎矩的幅值及其發生的位置。選擇恰當的參數，分別計算了實心樁和相等外徑的空心樁及與實心樁有相同等效截面積的空心樁在橫向動荷載作用下樁在任意截面的撓度、轉角、彎矩、剪力和土抗力集度。并對計算結果進行了對比分析（撓度曲線、轉角曲線、彎矩曲線、剪力曲線、土抗力集度曲線），得出以下結論：

（1）外徑相同的實心樁與空心樁相比，實心樁各截面的撓度和轉角較空心樁的小。

（2）外徑相同的實心樁與空心樁相比，實心樁各截面所受彎矩和剪力較空心樁的大。

（3）有效截面積相等的實心樁和空心樁相比，實心樁地面處的撓度和轉角幾乎是空心樁的2倍。

（4）有效截面積相等的實心樁和空心樁相比，實心樁各截面所受彎矩和剪力比空心樁的大且隨樁在土中的深度衰減較慢。

[1]胡人禮. 橋梁樁基礎分析和設計[M]. 北京：鐵道出版社，1987.

[2]趙明化. 橋梁地基與基礎[M]. 北京：人民交通出版社，2004.

[3]橫山幸滿. 樁結構物的計算方法和計算實例[M]. 北京：中國交通出版社，1984.

[4]盧世深，林亞超. 樁基礎的計算和分析[M]. 北京：人民交通出版社，1987.

[5]吳恒立. 計算推力樁的綜合剛度原理和雙參數法（第二版）[M].北京：人民交通出版社，2000.

[6]陳仲頤，周景星，王洪瑾. 土力學[M]. 北京：清華大學出版社，1994.

[7]戴自航，沈蒲生. 推力樁計算的綜合剛度雙參數法半數值解[J].福州大學學報，2004，32(6)：741-746.

[8]蔡婧，吳恒立. 推力樁動力響應的計算[J]. 工程力學，1999，3(a03)：741-746.