自適應笛卡爾網格Ghost Cell方法研究

劉劍明,趙 寧,胡 偶,王東紅

(1.南京航空航天大學航空宇航學院,江蘇南京 210016；2.徐州師范大學數學系,江蘇徐州221116)

0 引 言

眾所周知,計算流體力學中一個持續的障礙是復雜幾何外形的網格生成。現今存在的流場離散方法主要包括非結構網格方法、結構網格方法和笛卡爾網格方法[1]。雖然如今網格生成技術得到了進一步的發展,但網格生成過程仍然是一個費時費事的工作。非結構網格主要在二維流場使用三角網格,三維使用四面體或棱柱,其主要優點是易于生成復雜外形的網格,但非結構網格生成費時,計算時間存儲量一般都比結構網格高。結構網格單獨使用單一的貼體網格很難處理復雜外形,而且會導致網格的高度傾斜,因而一般不會使用單一的結構網格處理高度復雜的幾何外形,通常使用嵌套網格和多塊對接網格等,雖然這些方法已經得到了成功的使用,但它們需要交換不同網格間的數據,以及處理其他的一些復雜問題。使用笛卡爾網格方法,物體與背景網格切割,或者使用物體內部的虛擬控制體利用嵌入邊界來處理與物體的相交。切割網格需要考慮不同情形的復雜切割單元形狀,而且切割單元可能會任意小,從而會產生剛性以及時間步長穩定性問題。使用浸入邊界Ghost Cell方法可以克服小網格穩定性限制問題,而且更易于實現。笛卡爾網格相對于結構網格、非結構網格來說,具有更多的優勢,其網格生成簡單,易于實現自動化、具有更強的自適應能力,更適合于處理復雜幾何外形的繞流和由于物體運動或變形等產生的非定常問題,故本文研究笛卡爾網格方法。

最近Dadone和Grossman在他們的一系列文章[2-4]中,系統研究了結構網格中的Ghost Cell方法,并把他們命名為ST(Symmetry Technique)方法以及CCST(Curvature Corrected Symmetry Technique)方法,而且這些有效的邊界處理方法也被他們推廣用于笛卡爾網格[5-7],并取名為GBCM方法。后來,Dadone等[6]利用遠場網格加粗,以及Iblanking方法[8]進行自適應。在Wang的文章[9]中,此類方法也被用于二維非結構網格,得到了很好的結果。此外,Forrer[10,11]等提出了一種有趣的浸入Ghost Cell邊界方法求解二維靜止與運動物體。本文把ST方法以及GBCM方法用于自適應叉樹結構的笛卡爾網格,比較了Forrer的浸入邊界方法,Dadone的GBCM方法,以及其他的一些可用的邊界處理方法。數值結果顯示GBCM方法熵誤差最小,但總壓誤差和其他的邊界方法基本差不多,而且ST方法與GBCM方法的阻力系數相對于其他方法都較小。此外,本文利用基于叉樹結構的自適應笛卡爾網格Ghost Cell方法,求解一個強激波問題以及翼型,數值結果顯示本文所使用的自適應方法具有很好的分辨率,且易于實現。

1 控制方程和數值方法

本文僅研究無粘可壓流體,考慮二維歐拉方程

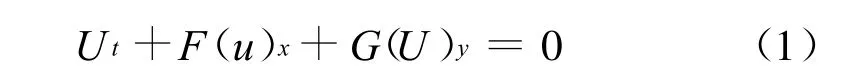
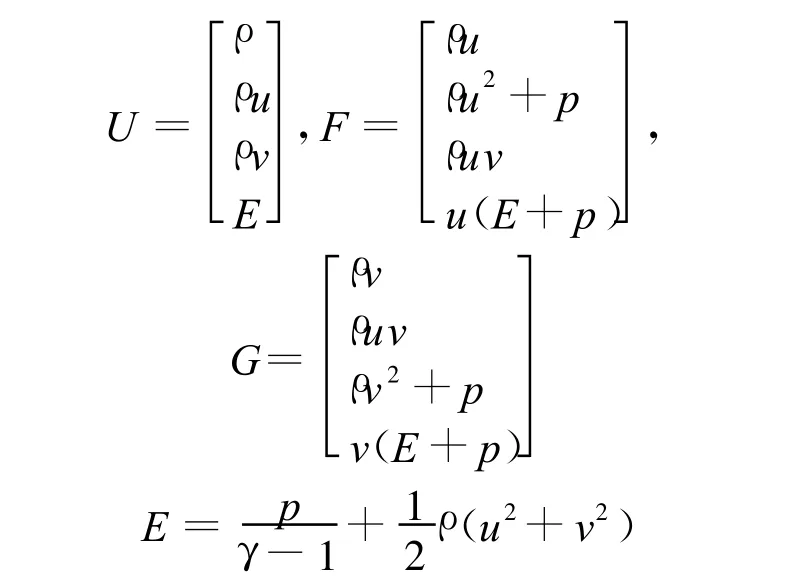
其中計算使用MUSCL方法加MINMOD限制器獲得高階精度,采用HLLC離散數值通量[12]

其中

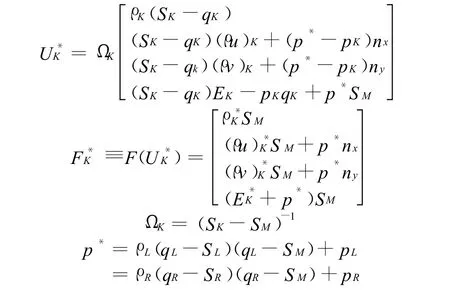
這里K=L,R,q≡unx+vny中間波速估計以及最大最小波速估計采用如下方法[13]

其中λ1(URoe),λ4(URoe)分別是 Roe矩陣[14]的最小最大特征值。在本文的數值模擬中,利用空間分裂法求解多維問題,使用最優二階 TVD Runge-Kutta方法[15]進行時間推進。

2 Ghost Cell方法

利用笛卡爾網格,物體與網格相交,如圖1所示。本文使用Ghost Cell方法需要給出浸入邊界(Immersed Boundary)內部網格點處的物理量,比如點A處的值。最直接最簡單的方法就是使用一般的對稱反射邊界條件(ST)

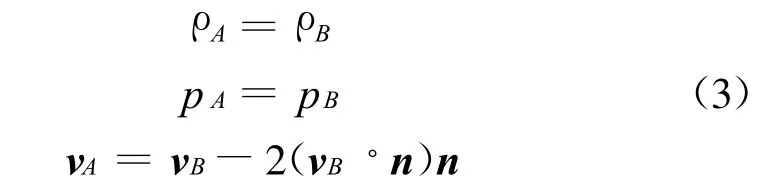
這里點B是A的鏡像點。這樣給出的邊界條件能夠滿足無穿透邊界條件vwall?n=0。Forrer等人[11]對于浸入固體內部的Ghost Cell值建議速度仍然使用一般的反射,而壓強密度使用如下公式

近來,Dadone與Grossman[5-7]系統的給出了一個新穎的Ghost Cell方法(GBCM)處理笛卡爾網格下的靜止物體。在他們的文章中,Ghost Cell物理量在墻附近通過一個法向假想的具有局部對稱分布的熵(S)與總焓(H)渦流場來得到。這種流體模型滿足如下法向動量方程

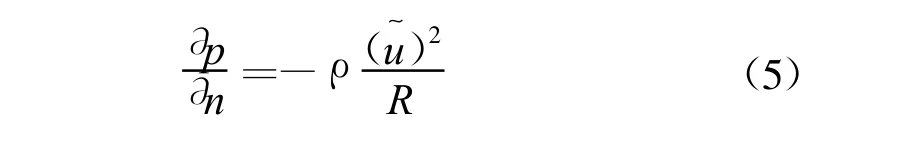
這里R是帶符號的局部曲率半徑,如果曲率中心在物體內部為正,反之為負。是切向速度,滿足無穿透邊界條件vwall?n=0,此外沿著物體的表面法向強加反對稱的熵與總焓的法向導數。這種熵與總焓分布使得當流動是無旋時,產生零法向導數,甚至在墻壁出現渦時也能滿足Crocco關系。比如對于二維問題,如圖1所示,采用如下邊界條件

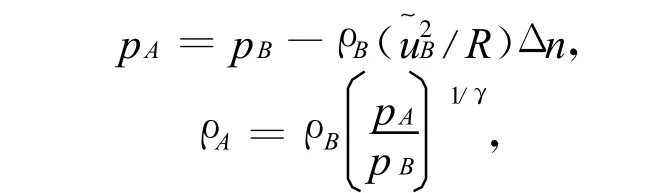
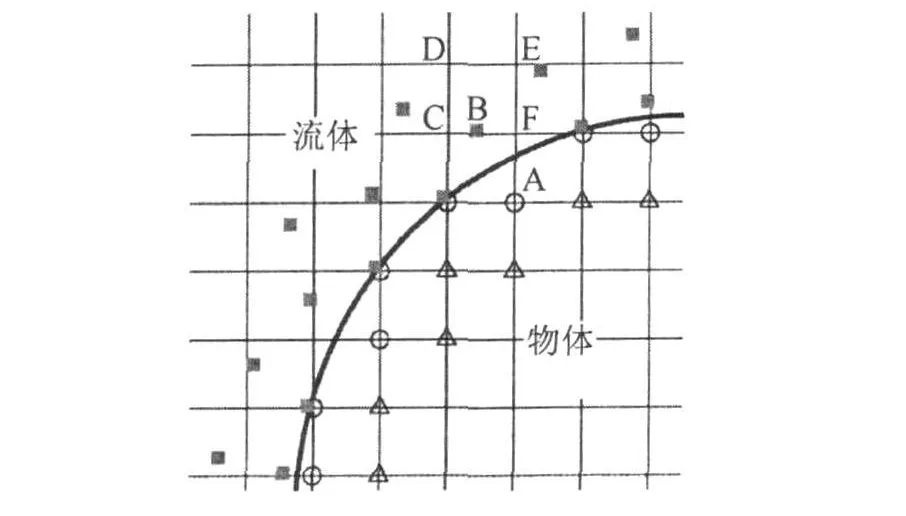
圖1 笛卡爾網格[5-7]Fig.1 Cartesian grid[5-7]

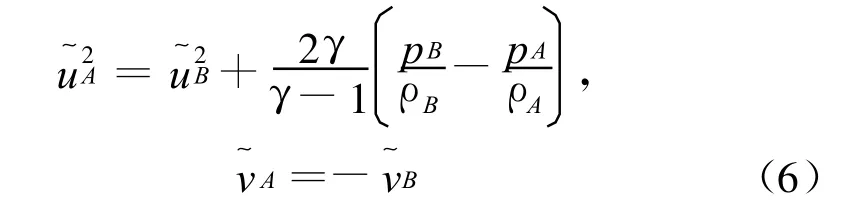
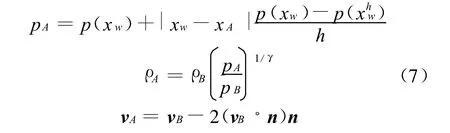
我們稱此方法為ECFGCM(Entropy Correction Forrer's Ghost Cell Method)方法,給出這個邊界條件的目的在于研究加了熵修正后是否真的能達到熵誤差的改善。

在數值計算中Ghost Cell中心A所對應的法向對稱點B變量的值可以通過一般插值得到,比如可以使用雙線性插值[5,6],或者利用權系數為距離倒數的線性插值公式,對于三維使用三線性插值[7]等,在我們的代碼中始終使用流體內部網格點插值。

3 各種Ghost Cell方法的數值比較

為了能夠比較各種不同的邊界方法,考慮亞聲速無粘流體吹向單位圓柱,來流馬赫數取為0.38,初始背景網格取為1/4個圓半徑,在圓柱附近作四次局部加密,如圖2(a)所示。圖2(b)給出了利用GBCM 方法得到的等馬赫圖,其他邊界處理方法的等馬赫圖基本相似,故省略。表1中給出了各種不同邊界方法所產生的熵與總壓相對誤差,從表中可以發現使用GBCM方法熵相對誤差要比其他方法約減少40%-70%,加了熵修正后的ECFGCM方法比FGCM稍好約減少20%。總壓誤差這幾種方法都差不多,ST情形稍微大一些。此外表1中還給出了不同邊界條件的阻力系數,從表1可以推知ST與GBCM方法阻力系數最小,分別是 3.01e-3與 4.58e-3。此外ST,FGCM,ECFGCM方法都很容易推廣到三維,而GBCM就不那么直接了。從計算復雜度考慮,ST方法計算最簡單,GBCM方法最復雜,尤其是在三維時,使用GBCM方法[7]需要計算物面與由流線在物面投影方向與物面法向所組成的平面交線的曲率,此外每一步需要進行坐標變換,Dadone的文章[7]給出了詳細的敘述。雖然Dadone的文章中指出GBCM方法具有稍好的結果,但對于一些復雜的幾何體,為了減少處理曲率的復雜性,尤其是三維問題,以及一些繁瑣的坐標變換,可以直接使用ST方法,一般就能得到可以接受的結果。為了和貼體網格的結果比較,我們直接引用文獻[9]中的結果。在文獻[9]中,Wang等人在非結構網格下使用Roe格式對同樣問題進行了計算,在他們的文章中利用128×32個四邊形貼體網格得出ST方法相對熵誤差與阻力系數分別為3.6e-3與8.0e-3。從我們的計算可以知道,笛卡爾網格的數目要比貼體網格多,計算時間要長一些。使用笛卡爾網格方法雖然網格不貼體,但得到的結果和傳統貼體網格方法的結果基本相當,能達到貼體網格的數值精度。

圖2 (a)局部加密圓柱笛卡爾網格,(b)GBCM方法(6)等馬赫線Fig.2 (a)Local refined Cartesian gird,(b)Mach contours of GBCM(6)

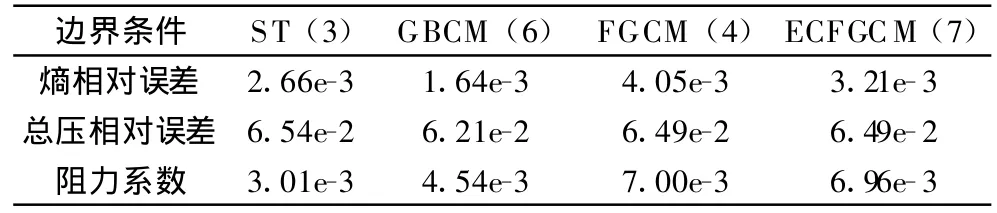
表1 相對誤差及阻力系數Table1 Therelativeerrors and drag coefficients

4 叉樹結構的自適應笛卡爾網格

為了更有效地處理一些復雜問題,本文把上述一些邊界處理方法用于基于叉樹結構的自適應笛卡爾網格,為了自動進行解自適應,使用如下自適應判據[17]

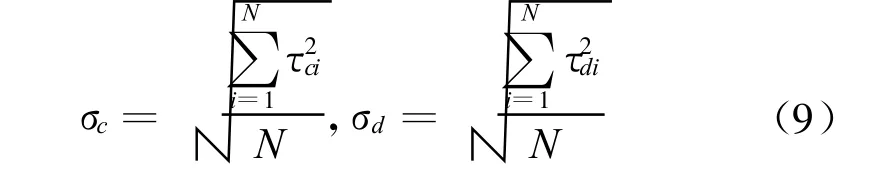
應用如下條件判定網格是否需要自適應:

(1)如果 τci＞σc或者 τdi＞σd,控制體 i被標記需要加細。

(2)如果 τci＜1/10σc且τdi＜1/10σd,控制體 i需要加粗。

為了驗證本文自適應加密代碼的有效性,考慮來流馬赫數為3的超聲速圓柱繞流問題,使用GBCM方法。圖3(a)顯示了幾何局部加密三次,解自適應加密三次后的網格圖,圖中精確捕捉了激波的位置,以及尾部需要加密的區域。圖3(b)顯示了壓強等值線圖。從圖中可以發現GBCM方法以及叉樹自適應方法能夠有效結合提高解的分辨率,尤其是激波的分辨率。此外為了顯示處理復雜幾何的能力,用本文方法計算了NACA0012翼型跨聲速繞流問題,這里取來流馬赫數 Ma∞=0.8,攻角 α=1.25°,自適應判據僅僅使用了速度散度。圖4(a)是解自適應加密三次后的網格圖,圖形清晰地顯示了強激波以及弱激波需要加密的位置,圖4(b)給出了等壓線圖,圖4(c)是壓力系數圖,圖形具有很好的激波分辨率。

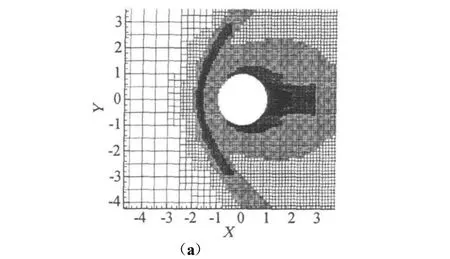
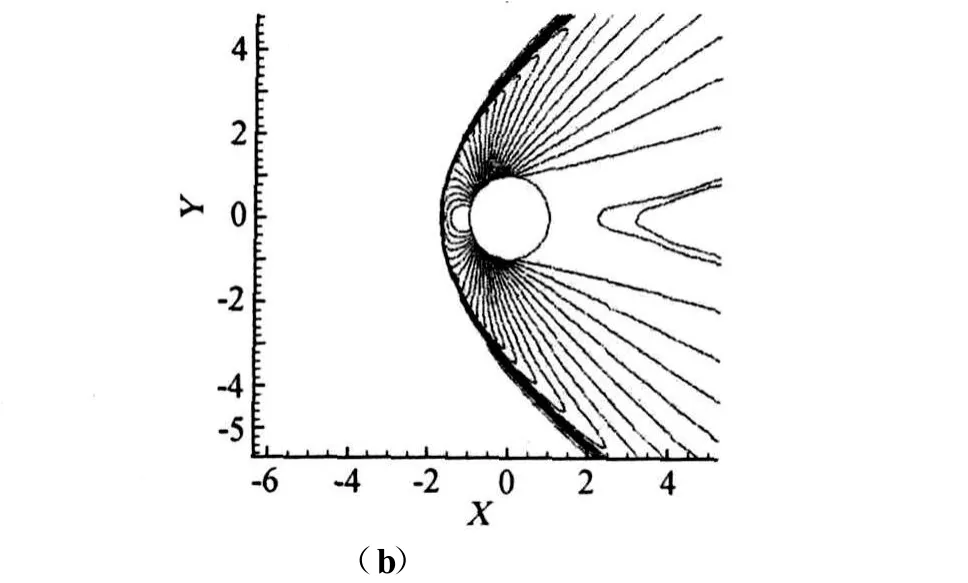
圖3 (a)三次解自適應加細后的網格,(b)壓強等值線Fig.3 (a)Adaptive Cartesian grid,(b)Pressure contours

圖4 翼型跨聲速繞流Fig.4 Transonic flow through airfoil

5 結 論

本文主要研究了Ghost Cell方法,比較了各種不同的Ghost Cell邊界條件的數值結果,并將其應用于叉樹結構的自適應笛卡爾網格,得到了理想的結果。數值實驗顯示本文方法是十分有效的,并且這些方法可以直接推廣到三維問題。

[1]KOH E PC,TSAI H M.Euler solution using Cartesian grid with a gridless least-squares boundary treatment[J].AIAA Journal,2005,43(2):246-255.

[2]DADONE A,GROSSMAN B.Surface boundary conditions for the numerical solution of the Euler equations[R].AIAA 93-3334.1993.

[3]DADONE A.Symmetry techniquefor the numerical solution of the2d Euler equations at impermeable boundaries[J].Int.J.Numer.Meth.Fluids.,1998,28(7):1093-1108.

[4]DADONE A,GROSSMAN B,Surface boundary conditions for thenumerical solution of the Euler equations in three dimensions[J].Lect.Notes.Phys.,1995,453:188-94.

[5]DADONE A,GROSSMAN B.Ghost-Cell method for inviscid two-dimensional flows on cartesian grids[J].AIAA Journal,2004,42(12):2499-2507.

[6]DADONE A,GROSSMAN B.Ghost-cell method with far field coarsening and mesh adaptation for Cartesian grids[J].Computers&Fluids,2006,35(7):676-687.

[7]DADONE A,GROSSMAN B.Ghost-cell method for inviscid three-dimensional flows on cartesian grids[J].Computers&Fluids,2007,36(10):1513-1528.

[8]DURBIN PA,IACCARINO G.An approach to local refinement of structured grids[J].J.Comput.Phys.,2002,181(2):639-53.

[9]WANG Z J,Yuzhi Sun,Curvature-based wall boundary condition for the Euler conditions on unstructured grids[J].AIAA Journal,2003,41(1):27-33.

[10]FORRER H,JELTSCH R.A higher-order boundary treatment for Cartesian-grid methods[J].J.Comput.Phys.,1998,140(2):259-277.

[11]FORRER H,BERGER M.Flow simulations on Cartesian grids involving complex moving geometries[A].Proc.Int.Conf.Hyp.Problems[C].Zurich,Switz,Feb.1998.

[12]BATTEN P,LESCHZINER M A,GOLDBERG U C.Average-state Jacobians and implicit methods for compressible viscous and turbulent flows[J].J.Comput.Phys.,1997,137(1):38-78.

[13]BATTEN P,CLARKE N,LAMBERT C,CAUSON D M.On the choice of wavespeeds for the HLLC Riemann solver[J].SIAM J.Sci.Comput.,1997,18(6):1553-1570.

[14]ROE P L.Approximate riemann solvers,parameter vectors and difference schemes[J].J.Comput.Phys.,1981,43(2):357-372.

[15]SHU C W.Essentially non-oscillatory and weighted essentially non-oscillatory schemes for hyperbolic conservation laws[R].NASA ICASE Report 97-65,1997.

[16]L?HNER R,BAUM J,MESTREAU E,SHAROV D.Adaptiveembedded unstructured grid methods[J].Int.J.Numer.Meth.Engng.,2004,60(3):641-660.

[17]DARREN L.DE ZEEUW.A quadtree-based adaptively-refined Cartesian-grid algorithm for solution of the Euler equations[D].[PhD thesis].The University of Michigan,1993.