軌道和波函數

黃正國徐梅芳

(1天津師范大學化學學院 天津 300387;2天津師范大學數學科學學院 天津 300387)

軌道和波函數

黃正國1＊徐梅芳2

(1天津師范大學化學學院 天津 300387;2天津師范大學數學科學學院 天津 300387)

分子(或原子)軌道是化學的基本概念之一。本文從 Bohr原子軌道入手,介紹軌道概念的演化,以及軌道與波函數之間的關系,分子軌道與原子軌道之間的關系,并結合量化計算介紹基組與分子軌道的關系。

分子 (或原子)軌道是化學中最常用的名詞之一。但是,根據量子力學原理,分子中電子的運動根本沒有確定的軌道,只能用波函數來描述其運動狀態。那么,化學中的分子軌道究竟是一個什么概念?它與波函數之間又有什么關系?本文將對這一問題加以論述。

1 Bohr原子軌道

人們對原子軌道的認識應該從原子結構談起。在 19世紀末,人們發現了電子,從而提出了各種原子結構模型,比如 Thomson的葡萄干模型,Rutherfold的行星繞日模型等,但都沒有成功地解釋原子的結構。1913年,Bohr提出了 Bohr原子模型,成功地解釋了氫原子的結構[1]。Bohr認為,在氫原子中存在許多定態,在每一種定態中,氫原子都是穩定的,此時電子繞原子核做圓周運動,原子既不吸收能量,也不輻射能量;而當氫原子在不同定態之間躍遷時,原子吸收(或輻射)能量,從而產生吸收 (或發射)光譜。雖然 Bohr原子模型成功地解釋氫原子的光譜,但它對多電子原子的光譜卻無能為力,也無法解釋氫原子光譜的精細結構。此外,在 Bohr的原子模型中,電子如同宏觀物體一樣,具有確定的軌道,這一點后來證明是錯誤的。盡管如此,為了便于理解和形象思維,電子在“軌道”上運動的說法還是保留了下來,但“軌道”的含義發生了很大的變化。

2 波函數和原子軌道

化學中的分子(或原子)軌道是根據量子力學理論提出來的,通常指的是分子 (或原子)的空間波函數。根據量子力學理論,波函數ψ是時間 t和空間 →r的函數,記作ψ(x,y,z,t)或ψ(→r,t),用于描述微觀粒子的空間運動狀態。不含時間的波函數稱為定態波函數,記做ψ(x,y,z)。定態波函數并不意味著粒子不運動,而表明粒子的運動狀態不隨時間而變。穩定的化學體系都可以用定態波函數來描述,因此,本文討論的主要是定態波函數。關于波函數的物理意義,有多種解釋,目前廣為接受的是 Born的統計解釋[2],即在某一時刻,空間某點粒子出現的概率密度正比于該時該點的波函數絕對值平方。因此,在分子 (或原子)體系中,將ψ2稱為概率密度 (即電子云),ψ2dτ為空間某點附近微體積元中電子出現的概率。

一般情況下,波函數是復數。但由于概率必須是實函數,所以一個合格波函數必須滿足以下條件:

①連續:粒子在空間各處出現的概率是連續變化的。

②單值:實物微粒在某一空間出現的概率是唯一的。

一個波函數全面規定了體系的各種性質,包含了體系各個物理量的信息。所以,如果知道了體系的波函數,也就可以獲得體系各個物理量的信息。但問題在于,可以獲得精確波函數的體系非常少,而對于絕大多數體系,只能獲得其波函數的近似解。

應該指出的是,波函數并非為電子所獨有,任何微觀粒子體系都可以用波函數來描述。例如,研究分子的振動光譜要用到振動波函數,該波函數與電子無關,是用來描述原子振動運動狀態的波函數。用于研究分子轉動光譜的轉動波函數也是如此。而勢箱波函數可以適用于電子、光子等許多微觀粒子。本文將主要討論電子波函數。此外,電子的波函數又可以分為空間波函數、自旋波函數和全波函數等等,而自旋波函數又稱為自旋軌道,全波函數又稱為旋-軌軌道,但是,一般意義上的分子(或原子)軌道指的是空間波函數。下面將具體介紹這幾種波函數的區別和聯系。

3 氫原子波函數和原子軌道

氫原子體系是為數不多的幾個能夠精確求解的體系之一,其 Schr?dinger方程的直角坐標形式如下:

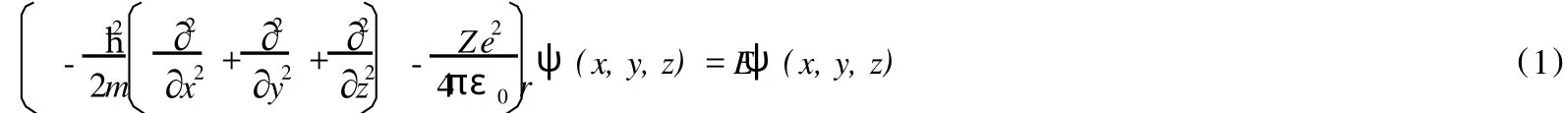
求解該 Schr?dinger方程,即可獲得氫原子的空間波函數。由于求得的空間波函數一般是復數,不便于作圖,因此通常可以根據態疊加原理,將復波函數進行線性組合,從而得到實波函數。下面列出了氫原子的幾個實波函數:

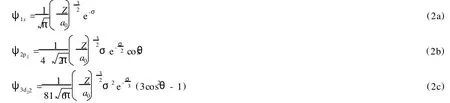
由于通常稱空間波函數為軌道,所以上述波函數依次為 s、p和 d軌道。

對于多電子原子體系,Schr?dinger方程無法精確求解,只能近似求解,通常采用單電子近似的方法,將含有N個電子的波函數簡化為N個單電子波函數:

從而求得近似解。由于每一個單電子波函數ψi都與氫原子波函數類似,所以多電子原子體系的實波函數同樣具有 s、p、d和 f形式。

上述波函數(或軌道)描述的是電子的空間運動狀態,并沒有考慮電子自旋的因素。如果考慮電子的自旋運動,用自旋波函數η來描述電子的自旋運動,則電子的整體運動狀態為空間波函數和自旋波函數的乘積:χi稱為全波函數,又稱為旋-軌波函數(或旋-軌軌道),η通常為α或β。可見,每一個空間軌道對應兩個旋-軌軌道,而每個旋-軌軌道上最多只能填充一個電子;根據 Pauli不相容原理,每一個(空間)軌道上最多只能填充兩個自旋相反的電子。

4 體系總波函數的反對稱性和 Slater行列式

電子屬于費米子。多電子體系的總波函數遵守反對稱性的要求,也就是說,如果交換體系中任意兩個電子的全部坐標(包括空間坐標和自旋坐標),則新的總波函數為原總波函數的負值。但是,如果單個電子的全波函數僅僅采用(4)式,則多電子體系的總波函數并不一定能夠滿足反對稱性條件。因此,必須構建一種新的能夠滿足反對稱性條件的總波函數。下面以 He原子為例作一簡要介紹[3]。

He原子體系的基態空間波函數為ψ1s(1)ψ1s(2),自旋波函數為α(1)β(2),則 He原子體系的總波函數為ψ1s(1)ψ1s(2)α(1)β(2),但該總波函數不滿足波函數的反對稱性條件。為了滿足波函數的反對稱性條件,如果空間波函數是對稱的,則自旋波函數必須是反對稱的,反之亦然。對于 He原子體系的空間波函數,如果交換兩個電子的空間坐標,則有:

所以,He原子體系的空間波函數是對稱的,這就要求其自旋波函數必須是反對稱的。如果 He原子體系的自旋波函數仍為α(1)β(2),則交換兩個電子的自旋坐標,有:

所以,He原子體系的自旋波函數既非對稱的,又非反對稱的。考慮到電子的全同性,He原子體系的自旋波函數有兩種可能:α(1)β(2)或α(2)β(1)。根據態疊加原理,這兩種自旋波函數的線性組合仍然是 He原子體系的一種可能的狀態:

取滿足反對稱性條件的自旋波函數(8),則 He原子體系的總波函數為:

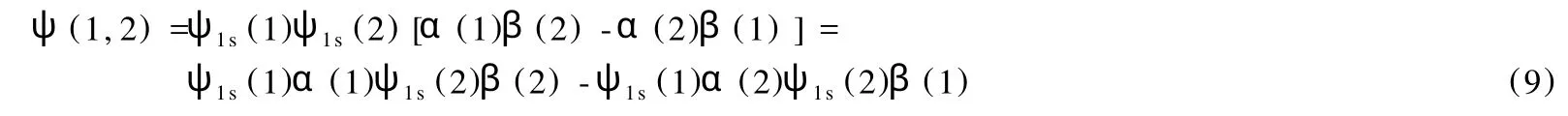
歸一化后,可以寫成如下 Slater行列式:

可見,采用 Slater行列式形式描述的體系總波函數能夠滿足反對稱性條件。

對于含有N個電子的原子體系,其體系總波函數仍然可以用 Slater行列式來描述:

應該從態疊加原理來正確理解 Slater行列式。將 Slater行列式展開,可得:

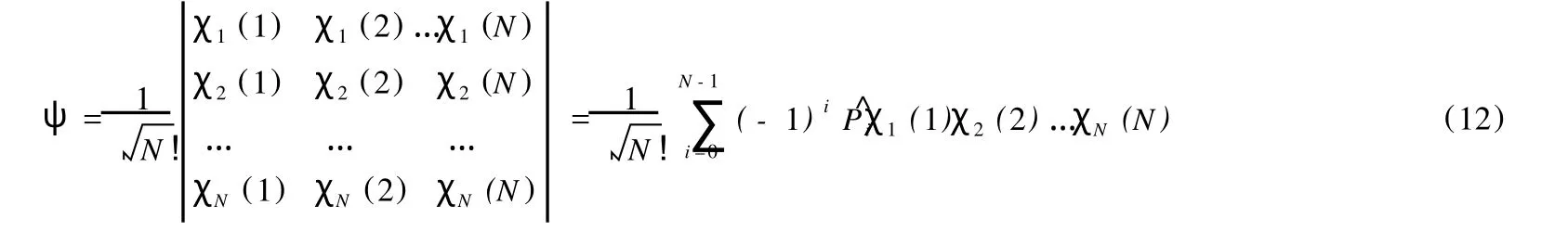
5 分子波函數(分子軌道)與原子波函數(原子軌道)的關系

根據分子軌道理論,分子軌道即為分子體系的單電子空間波函數,是由原子軌道線性組合得到的,稱為原子軌道線性組合成分子軌道 (linear combination of atomic orbitals,LCAO)[1]:

其中ψ為分子軌道,φi為原子軌道。原子軌道線性組合成分子軌道時,軌道的數目不會發生變化,即 n個原子軌道通過線性組合必然得到 n個分子軌道,但軌道的能級發生了變化。通常把能級低于原子軌道的分子軌道稱為成鍵分子軌道,反之則稱為反鍵分子軌道。除此之外,還有非鍵分子軌道,即分子軌道能級等于原子軌道的能級。所以,在 n為偶數時形成的分子軌道中,一半是成鍵分子軌道,另一半是反鍵分子軌道;而 n為奇數時,則會出現非鍵分子軌道。成鍵分子軌道、反鍵分子軌道以及非鍵分子軌道的不同主要在于 (13)式中原子軌道系數 ci的不同。

此外,并非任意原子軌道都能組合成分子軌道,分子軌道的形成要遵守 3條原則:能級高低相近原則、最大重疊原則和對稱性匹配原則。其中對稱性匹配原則是首要的,它決定原子軌道能否組合成分子軌道,而其他兩條原則決定組合成什么樣的分子軌道以及組合的效率。關于這一問題,已有文章專門論述[4],本文不再詳述。

6 分子軌道和基組

在實際的量化計算中,很少真正使用 Slater行列式表示體系波函數,而一般采用有限基組(basis set)表示波函數 (或軌道)[5]。

根據式(13),原子軌道可以線性組合成分子軌道,但在實際的量化計算中,往往不是采用真正的類氫離子波函數作為原子軌道,而是采用一組基函數用于線性組合分子軌道:

φj稱為基組 (也叫基集,基函數等),系數 cji有待 SCF方法進行優化。原則上φj并不局限于類氫離子波函數,任何一組函數的完備集都可以選為基函數。當然,出于實際考慮,合適的基函數應該滿足以下要求:

①是真實波函數的有意義的反映;

②預測的能量能夠達到化學精度 (一般認為是 8kJ·mol-1);

③在實際計算中所耗用的時間比較適中;

④可移植性強,即能夠適用不同的成鍵環境。

采用類氫離子波函數作為基函數,在進行分子軌道計算時,由于徑向部分的關聯 Laguerre多項式積分難以計算,迭代收斂很慢,并不適用于實際計算。實際量化計算中,經常使用的基函數主要有兩種類型,一種是 Slater型軌道 (Slater type orbital,STO),另一種是 Gaussian型軌道(Gaussian type orbital,GTO)。這兩種類型的基函數各有特點,但 GTO的使用范圍較 STO更為廣泛。

在量化計算中,由于類氫離子波函數的技術瓶頸在徑向函數部分,所以 Slater對其加以改造,提出了新的徑向函數,稱為 STO:

其中ξ是軌道指數,r為電子到該 STO所在核的距離,n為主量子數。采用 STO可以大大減少計算積分時數學處理的復雜性。但是,與類氫離子波函數不同,STO沒有徑向節面,所以單一的 STO不能很好地逼近原子軌道,必須采用 STO的線性組合,才能更好地擬合原子軌道:

一般 3～5個不同ξi的 STO能很好描述一個原子軌道,但實際計算中一般只有 2～3個。

在 r→∞和 r→0時,STO具有正確的波函數漸近行為,但 STO也有一個重大缺點:在多原子分子中,大量的 3中心和 4中心積分難以解析求算。針對這種情況,Boys在 1950年提出使用 Gauss函數(GTO)。GTO可寫為笛卡爾坐標的形式:

其中α是軌道指數,r為電子到該 STO所在核的距離,x,y,z為笛卡爾坐標,lx,ly和 lz是簡單的整數而不是量子數,且滿足下列關系式:

GTO與 STO的差別在于指數函數 e-α(x2+y2+z2)和 e-αr。GTO只有 1s,沒有 2s和 3s,而 p型函數也只有 2p,沒有 3p和 4p等,即 GTO與原子軌道沒有一一對應關系。GTO的優點在于很容易分離變量,并且積分方便,可以將 3中心和 4中心積分化作雙中心積分,最后化作單中心積分來處理,從而使多電子分子體系中的許多問題得以解決。正是因為使用 GTO具有計算上的優勢,當今的絕大多數量化計算都是在 GTO下進行的。目前,在主流的商業量化軟件中,都收集了許多基組,其中大多數是采用 GTO的基組,例如價層劈裂基組 3-21G、6-31G等。

在基組中,一個基函數代表一個軌道。小基組中的基函數數目比較小,而大基組中基函數的數目大,但是無論采用大基組還是小基組,占據軌道數是固定不變的,而空軌道的數目隨著基組的增大而增多。從數學上嚴格講,式 (14)中的φj應包含所有可能的原子軌道,但太復雜,所以用一些主要的占有軌道和價軌道,稱為有限基組。使用有限基組進行量化計算,必然會帶來一定的誤差,這種誤差一般隨著基組的增大而減小,所以,一般而言,基組越大,計算結果越接近真實,但計算的困難也越大(積分數目與基組數目 n4成正比),所以在實際計算中要在計算效率和計算精度二者之間取平衡。

[1] 周公度,段連運.結構化學基礎.第 4版.北京:北京大學出版社,2008

[2] 潘道皚,趙成大,鄭載興.物質結構.第 2版.北京:高等教育出版社,1989

[3] 林夢海.量子化學簡明教程.北京:化學工業出版社,2005

[4] 黃輝.楚雄師范學院學報,2002(6):42

[5] 聶麗,張強.大學化學,1997,12(2):53

[6] 陳光巨,黃元河.量子化學.上海:華東理工大學出版社,2008

＊ 通訊聯系人,E-mail:hxxyhzg@mail.tjnu.edu.cn