基于相位相關的亞像素配準技術及其在電子穩像中的應用

孫 輝,李志強,孫麗娜,郎小龍

(中國科學院長春光學精密機械與物理研究所,吉林長春 130033)

1 引 言

圖像配準是一種基于傅里葉功率譜的頻域相關技術,是由 Kuglin和 Hines在 1975年提出來的[1]。近幾十年來,廣大專家學者在圖像配準方面做了深入的探索和研究,在優化算法、提高配準精度等方面提出了許多行之有效的方法。在各種圖像配準方法中,基于相位相關的配準方法以其算法簡單易行、運算量小、配準精度高等優點在學術界受到極大關注,在醫學圖像處理、遙感圖像處理、計算機視覺、運動分析、工業檢測等領域得到了廣泛應用。

圖像配準可以將來自不同時間、不同角度或不同數據源的幾幅圖像對準,一般可實現像素級配準精度,滿足實際應用要求。盡管如此,在很多應用領域,為提取更準確的圖像信息,通常需要亞像素級的配準精度。文獻[2]提出了一種擴展的相位相關法,即在相位相關法基礎上,通過理論分析將其擴展到亞像素級配準精度。由于該方法只提取互功率譜中的相位信息,減少了對圖像內容的依賴,具有較強的抗干擾能力,是目前廣泛使用的頻域配準方法[3～10]。

本文針對序列圖像中的圖像失穩問題,將基于擴展的相位相關圖像配準技術用于檢測視頻圖像幀間亞像素級的運動量,然后對圖像進行亞像素級的運動補償,輸出平滑、穩定的視頻圖像。與像素級的運動檢測和補償相比,本文方法可實現更高的穩定精度,有效提高了圖像補償質量。

2 亞像素配準技術

2.1 相位相關配準原理

設f1(x,y)為基準圖像,f2(x,y)為f1(x,y)平移(x0,y0)后的位移圖像,兩者滿足如下關系:

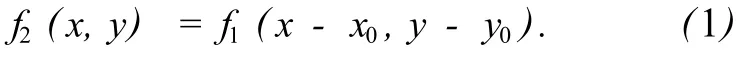
對式 (1)做傅里葉變換,有:

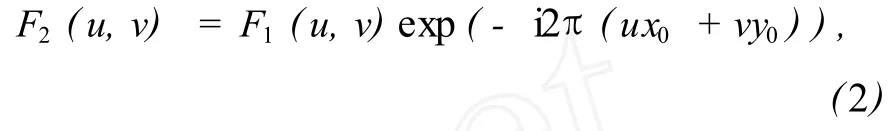
式中F1(u,v)和F2(u,v)分別表示f1(x,y)和f2(x,y)的傅里葉變換。

因此,兩幅圖像之間歸一化的交叉功率譜可表示為:

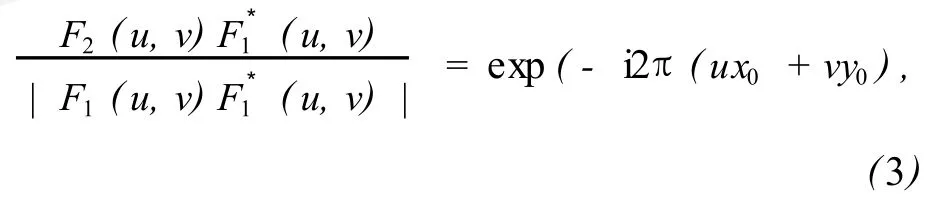
式中＊表示復共軛,將式 (3)兩端進行傅里葉逆變換,可得相位相關函數如下:

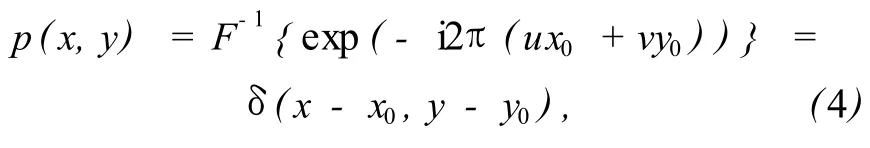
式中δ(x-x0,y-y0)為典型的 Dirac函數,也稱沖激函數,該函數在中心點(x0,y0)處不為零,在其它位置均為零。圖1顯示了相位相關函數曲線,其中圖1(a)顯示了位移等于 0像素的相關曲線,圖1(b)顯示了在水平方向產生 0.5像素位移情況下的相關曲線。

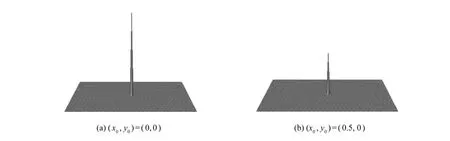
圖1 相位相關函數 p(x,y)Fig.1 3D plots of phase correlation functionp(x,y)

在實際應用時,由于傅里葉變換對f(x,y)的周期性有要求,而實際圖像一般都不具備周期特性,所以為減小邊緣效應對配準精度的影響,需采用加窗技術,即對輸入圖像進行適當加權處理,使其具有周期性特征,以符合傅里葉變換條件。

典型的 2D Hanning窗定義如下:

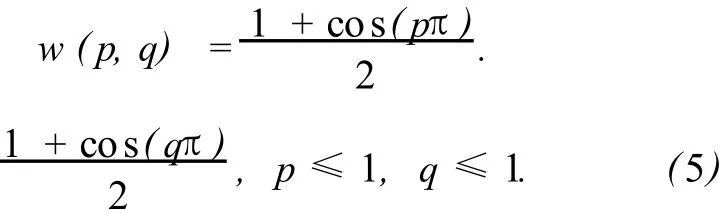
將上述形式的加窗函數作為加權系數,分別作用于f2(x,y)和f1(x,y)并進行傅里葉變換,可較好地減小邊緣效應。

2.2 亞像素精度檢測

常規的頻域相關配準算法只能檢測到像素級的平移運動量,為獲取亞像素級運動量,本文采用基于最小二乘法的二次曲面擬合方法,通過在相關峰值坐標點附近用曲面擬合相位相關值,擬合曲面的峰值坐標即為平移運動參數。

根據上述分析,本文選擇如下擬合函數:

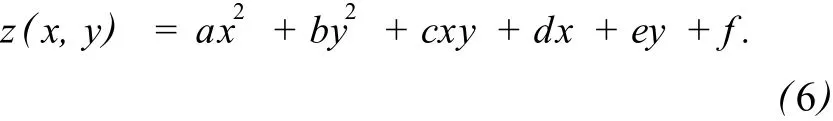
擬合函數z(x,y)的系數可通過解下列方程解出:

式中:

采用最小二乘法求解方程,即可解出擬合函數的系數。

為此,在式 (6)中分別對x,y求偏導,并使偏導為 0,即:

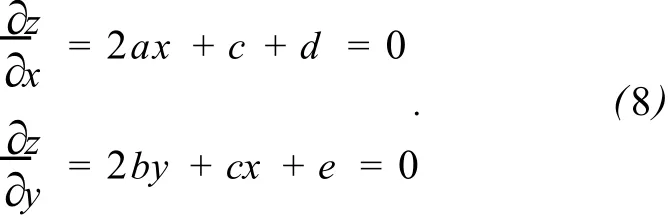
由式 (8)可解得:

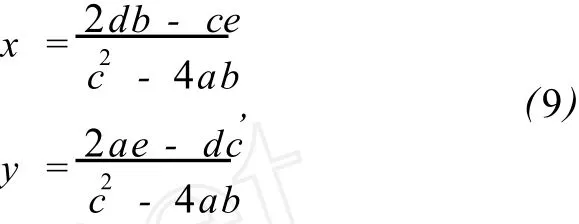
式中的x,y即為所求的平移量且具有亞像級的分辨率。

2.3 亞像素補償

序列圖像運動補償是根據圖像運動矢量,對圖像像素位置進行重組實現的。通常,圖像之間的運動包括平移運動、旋轉運動、尺度變換及仿射變換等,本文只討論平移運動情況。在平移運動中,兩幅圖像只有水平和垂直方向的運動變化,按照運動方向等量反向移動圖像即可實現運動補償。

設位移圖像g(x,y)通過運動補償得到結果圖像f(x,y),則f(x,y)和g(x,y)建立一一對應關系 ,即:

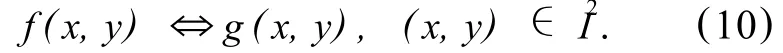
當平移量為亞像素時,(dx,dy)∈R2,圖像平移運動補償公式如下:

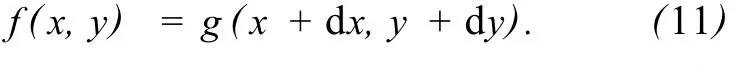
采用式 (11)進行圖像補償,對于f(x,y)的每一個像素坐標(x,y),都可以保證在g(x,y)中有一個對應的像素點坐標 (x+dx,y+dy)。由于x+dx和y+dy是小數,而g(x,y)圖像坐標是整數,所以在補償圖像時,不能簡單地進行整數坐標映射,要根據平移運動量進行適當的平滑處理,否則在小數轉化為整數的過程中將產生誤差,影響圖像補償精度。

為了提高補償質量,采用雙線性插值方法對圖像像素灰度值進行了平滑處理,根據位移圖像坐標 (x+dx,y+dy)與四鄰域位置及灰度值的對應關系,通過四鄰域灰度值加權平均的方法計算f(x,y)的像素灰度值。

雙線性插值公式如下:

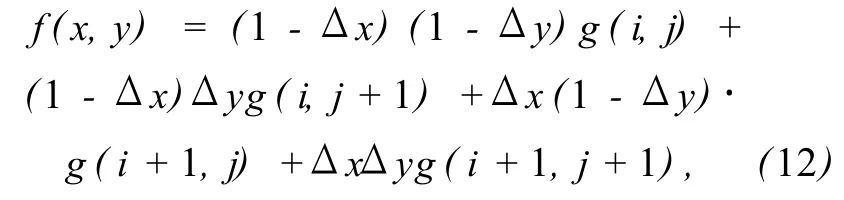
式中i,Δx分別表示x+dx的整數部分和小數部分,j,Δy分別表示y+dy的整數部分和小數部分 ,即 Δx=x+dx-i,Δy=y+dy-j。采用雙線性插值處理后的圖像邊緣清晰、完整、無鋸齒,具有較好的補償效果。

3 仿真實驗結果

為檢測亞像素檢測精度及穩像效果,在實驗室進行了仿真實驗。

樣本圖像選用標準樣本圖像庫中的 bridge圖像,原始圖像見圖2(a),對比圖像通過對原始圖像進行平移得到。為檢測本文方法對亞像素運動量的檢測精度,研究人員在水平和垂直方向上同時對原始圖像進行步長為 0.01 pixel的平移操作,一共生成 50幀對比圖像,其中第一幀位移dx=dy=0.01 pixel,第 50幀位移 dx=dy=0.5 pixel,如圖1(b)、圖1(c)所示。圖像位移曲線見圖3。

圖2 樣本圖像Fig.2 Sampling images

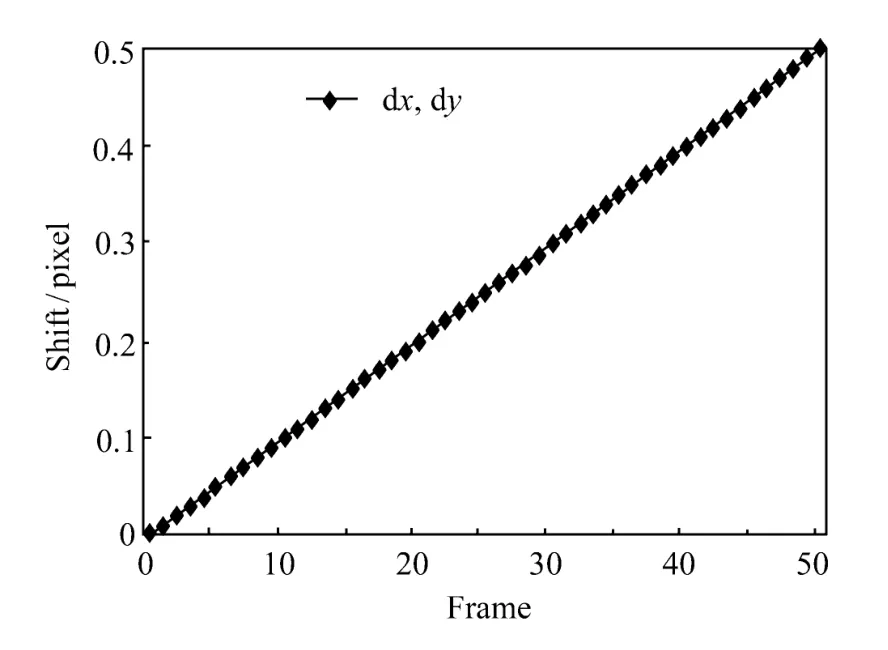
圖3 亞像素位移曲線Fig.3 Curve of sub-pixel displacement

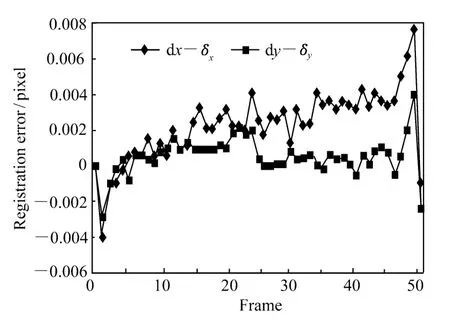
圖4 運動量檢測誤差曲線Fig.4 Errors in displacement estimation

采用本文介紹的圖像配準算法對樣本圖像進行運動量檢測,計算從第 1幀到第 50幀對比圖像相對原始圖像的亞像素級的運動矢量 (δx,δy),由于每幅對比圖像相對參考圖像的真實位移量已知,可以統計配準結果與真實位移量的誤差,配準誤差統計結果如圖4所示。通過圖4中的誤差曲線可以看出,在 50個位移矢量檢測結果中,與真實位移量的最大誤差僅為 0.008 pixel。

采用上述亞像素運動量和式 (12)進行圖像運動補償,用均方根誤差 (Root of Mean Square Error,RMSE)作為客觀指標評價電子穩像效果,對 50幀樣本圖像分別統計補償后的均方根誤差值,統計結果見圖5。從統計數據和誤差曲線可以看出,補償前最大誤差為 12.8 pixel,經過亞像素級運動量檢測和圖像補償后,最大誤差僅為0.5 pixel,有效提高了圖像補償質量。

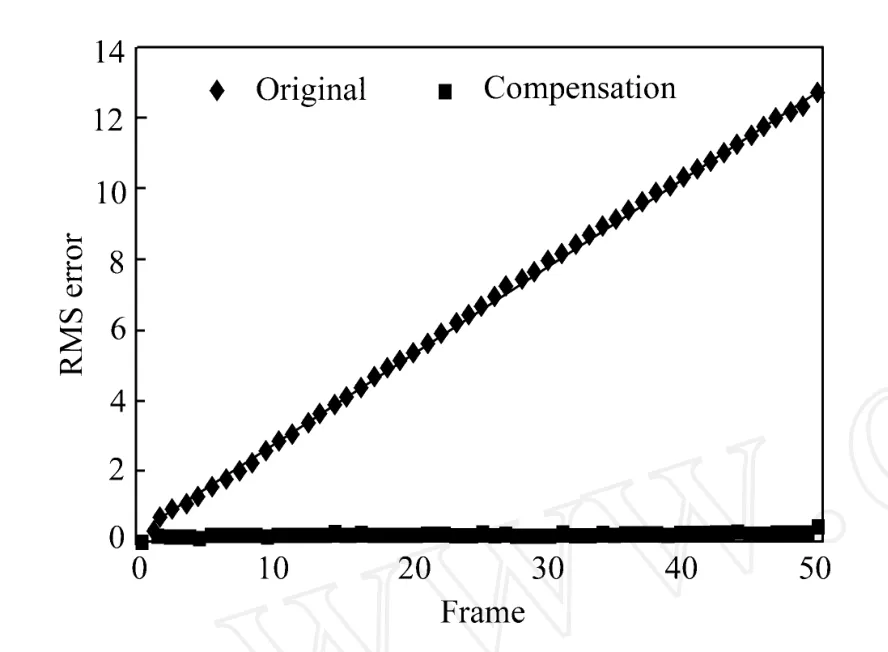
圖5 圖像補償誤差曲線Fig.5 RMS errors of compensation

4 結 論

本文介紹了基于相位相關的圖像配準方法,并將該方法應用于視頻序列圖像的亞像素運動檢測,通過雙線性插值技術補償亞像素運動量。實驗結果表明,相位相關算法利用圖像的互功率譜信息,減少了對圖像內容的依賴,具有較強的抗噪能力;同時該算法具有亞像素級的配準精度,提高了圖像運動的檢測精度,通過亞像素圖像補償技術,可有效提高圖像補償質量和穩像效果。

[1] KUGL IN CD,H INESD C.The phase correlation image alignment method[A].Proc.Int.Conf.Cybernetics Society[C].San Francisco,USA,1975:163-165.

[2] FOROOSH H,ZERUB IA J,BERTHOD M.Extension of phase correlation to sub-pixel registration[J].IEEE Trans.Im age Processing,2002,11(3):188-200.

[3] 桂志國,韓焱.相位相關配準法及其在射線圖像數字減影中的應用[J].儀器儀表學報,2004,25(4):520-522.GU I ZH G,HAN Y.Phase correlation technique for image registration and its application in dsa of radiographic image[J].Chinese J.Sci.Instrum.,2004,25(4):520-522.(in Chinese)

[4] 高世海,戴文剛,田仲.空域和頻域相結合的景象匹配算法[J].中國圖象圖形學報,2000,5(A)(4):345-348.GAO SH H,DA IW G,T IAN ZH.Hybrid image registration algorithm of space domain and frequency domain[J].J.Im age Graphics,2000,5(A)(4):345-348.(in Chinese)

[5] 吳元昊,于前洋.基于傅里葉相位差的抗噪聲位移估計算法[J].光學精密工程,2007,15(7):1137-1142.WU Y H,YU Q Y.Denoising algorithm of displacement estimation based on phase difference of Fourier transform[J].Opt.Precision Eng.,2007,15(7):1137-1142.(in Chinese)

[6] 馮林,管慧娟、藤弘飛.基于互信息的醫學圖像配準技術研究進展[J].生物醫學工程學,2005,22(5):1078-1081.FENGL,GUAN H J,TENG H F.Advances in medical image registration based on mutual information[J].J.B iom edical Eng.Res.,2005,22(5):1078-1081.(in Chinese)

[7] 周永新,羅述謙.基于形狀特征點最大互信息的醫學圖像配準 [J].計算機輔助設計與圖形學學報,2002,14(7):654-658.ZHOU Y X,LUO SH Q.Medical image registration based on mutual infor mation of feature points[J].J.Com puter-A ided Design Com puter Graphice,2002,14(7):654-658.(in Chinese)

[8] 李治國,安錦文,趙銀鈴.基于相位相關的全局運動估計算法[J].計算機測量與控制,2008,16(4):532-534.L I ZH G,AN J W,ZHAO YL.Globalmotion est imation algorithm based on phase correlation[J].Com puterM easurem ent Control.,2008,16(4):532-534.(in Chinese)

[9] 黎俊,彭啟民,范植華.亞像素級圖像配準算法研究[J].中國圖象圖形學報,2008,13(11):2071-2075.L IJ,PENGQ M,FAN ZH H.Asurvey of sub-pixel image registration methods[J].J.Im age and Graphics,2008,13(11):2071-2075.(in Chinese)

[10] 徐寶昌,陳哲,趙龍.一種改進的最小二乘景象匹配算法[J].北京航空航天大學學報,2005,31(8):848-852.XU B CH,CHEN ZH,ZHAO L.Inproved least-squares acene matching algorithm[J].J.Beijing University Aeronautics and Astronautics,2005,31(8):848-852.(in Chinese)