基于物質躍遷能壘改進正常晶粒長大的Monte Carlo模擬

劉建元，張曉泳，周科朝

(中南大學 粉末冶金國家重點實驗室，長沙 410083)

基于物質躍遷能壘改進正常晶粒長大的Monte Carlo模擬

劉建元，張曉泳，周科朝

(中南大學 粉末冶金國家重點實驗室，長沙 410083)

在采用改進的Monte Carlo方法模擬正常晶粒的長大過程時，考慮到實際晶粒長大過程中物質狀態躍遷需克服一定能壘，把躍遷能壘引入到狀態躍遷概率計算中，使模擬過程所含物理意義更為明確。模擬結果表明：在各種模擬條件下得到的模擬晶粒長大指數為0.472～0.493，接近理論的晶粒長大指數(0.5)。改變模擬溫度和能壘等模擬條件后，得到的晶粒形貌演變過程、晶界分布拓撲特征以及晶粒長大速率等模擬結果也均與晶粒長大動力學相關理論和實際晶粒長大規律相吻合。

Monte Carlo方法；晶粒長大模擬；晶粒長大指數；躍遷概率；物質躍遷能壘

Abstract:Considering that an energy barrier should be conquered to realize the mass transition during the real grain growth process, the Monte Carlo method was modified by introducing the energy barrier for mass status transition into the evaluation of mass fransition probability to simulate the normal grain growth. The aim of modification was to improve the physical significance of simulation. The simulation results show that the simulated grain growth exponent is 0.472?0.493, which is close to the theoretical value of 0.5. With the variation of simulation temperature and energy barrier, the simulation results about the grain morphology development, the topological characteristic of grain boundary and the variation of grain growth rate are all in accordance with the theories and real rules of normal grain growth kinetics.

Key words:Monte Carlo method; simulation of grain growth; grain growth exponent; transition probability; energy barrier for mass transition

Monte Carlo方法(簡稱MC)因具有模擬實現方法和程序設計簡單、模擬速度相對較快以及能夠利用計算機圖形學直觀描述微觀結構等諸多優點，被廣泛用于晶粒長大過程的模擬研究[1?6]。在MC模擬過程中，首先，建立離散化模擬對象，并賦予每個格點某一取向度值，由取向度值相同的相鄰格點組成晶粒，由每對取向度不同的相鄰格點組成晶界；然后，隨機選取晶界處的格點，并嘗試賦予其新取向度值，通過計算由此引起的晶界能變化，得到賦予被選格點新取向度值的概率，以此決定是否賦予被選格點新取向度值，進而實現物質在晶界處躍遷以及晶界遷移的模擬。對所有格點遍歷處理一次即為一個模擬時間步(MCS)，并最終模擬出整個晶粒的長大過程。

在目前大多數文獻所報道的MC模擬晶粒長大研究中，在給定模擬溫度時，所得模擬結果與實際晶粒長大過程中的微觀結構拓撲演變關系較為相符，且模擬的晶粒長大指數也接近理論長大指數(0.5)[6?9]。但是在模擬不同溫度下的晶粒長大過程時，會出現模擬溫度升高引起晶粒長大速率減慢這一與實際現象不符的模擬結果[10]。為此，文獻[11?13]建立了如下的模擬時間—真實時間的線性和非線性對應關系：

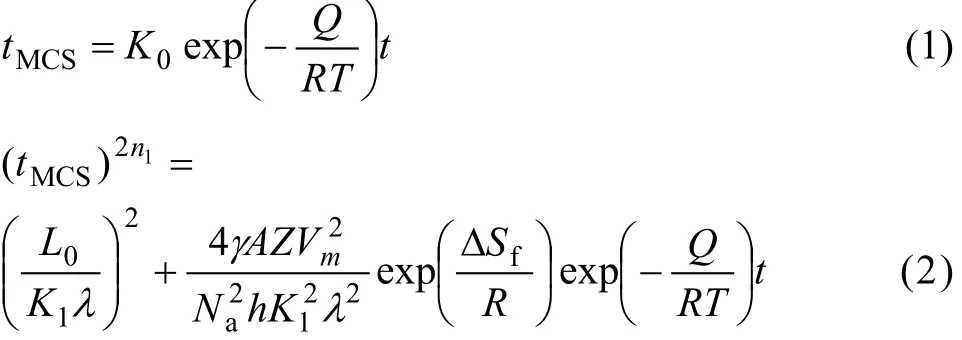
式中：tMCS為模擬時間；T和t分別為真實溫度和時間；A、K1和n1都為建模系數；K0為與原子振動頻率相關的常數；Q為激活能；Z為單位晶界面積上原子的平均個數；Vm為原子體積；γ為晶界能；L0為初始平均晶粒尺寸；ΔSf為融化熵；λ為陣點距離；Na為阿伏伽德羅常數；R為摩爾氣體常數；h為普朗克常數。利用上述對應關系可模擬出不同溫度和升溫速率下的正常晶粒長大過程。但在其模擬處理方式中，只涉及格點重新賦值后需降低晶界能這一要求，并沒有考慮格點重新賦值要克服一定能壘以及格點通過能量起伏并克服能壘后有可能向高能態躍遷這兩點，與實際晶粒長大過程中的物質狀態躍遷在一定程度上不相符[14]。與此同時，針對原有MC模擬方法中躍遷概率計算存在的一些問題，文獻[15?17]提出了新的躍遷概率計算表達式。但這些擬合公式缺乏較為真實的物理含義。如文獻[16]提出了如下擬合公式：

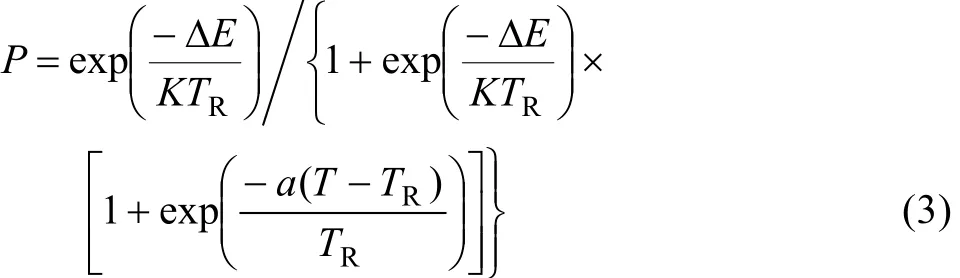
式中：ΔE為格點重新賦值前、后晶界能的變化；TR為材料再結晶溫度；a為擬合系數；K為波爾茲曼常數。

針對這些研究現狀，本文作者首先分析原有的MC模擬方法中因模擬處理方式與實際物質躍遷過程不符而導致出現的一些問題，然后提出相應的改進措施，將物質在躍遷前需克服一定能壘這一因素在躍遷概率計算過程中直接體現，使模擬過程的物理含義更為明確，并用于模擬不同溫度下的晶粒長大過程。

1 模擬過程

圖1給出了MC模擬晶粒長大過程中用于描述微觀結構格點集合的示意圖。其中如果某一格點周圍存在取向度值與之不同的其它相鄰格點，則該格點位于晶界處，有可能被改變取向度值狀態，進而引起晶粒長大和晶界遷移。

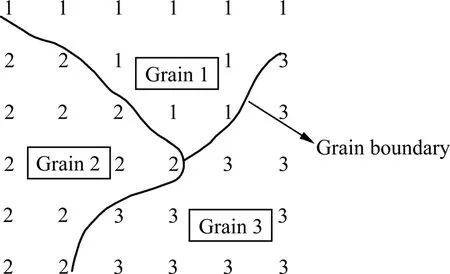
圖1 MC模擬晶粒長大過程中用于描述微觀結構格點集合的示意圖Fig.1 Schematic of lattice integration representing microstructure in MC method to simulate grain growth

目前，大多數MC模擬晶粒長大研究中的躍遷模擬示意圖如圖2所示。對于圖2中取向度值為2的中間被選格點i，首先賦予其周圍與之不同的格點取向度值為1，并計算取向度值改變后引起的晶界能變化ΔE：

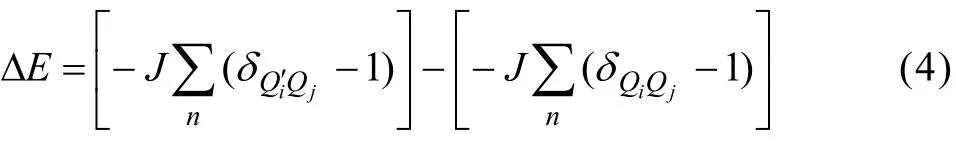
式中：J為晶界能；Qi和Qi′分別為被選格點i重新賦值前、后的取向度值；n為與格點i相鄰的格點數；Qj為相鄰格點的取向度值；δ為Kronecker算符(Qi或Qi′ ≠Qj時δ= 0；Qi或Qi′ =Qj時δ= 1)。若 ΔE≤0，則賦予格點i新取向度值Qj，即引起晶界處的物質遷移，并使總晶界能減小；若ΔE＞0，則計算格點i是否接受新取向度值Qj，進而得到引發高能態躍遷的Boltzman概率(P)，然后，在(0, 1)產生一個隨機數W；當P≥W時，賦予格點i新取向度值Qi′，否則，仍保持原有取向度值。

式中：k為Boltzman常數；T為模擬溫度。

通過分析可以發現，在上述躍遷模擬處理方式中，隨著模擬溫度T的升高，式(2)中物質向高能態躍遷的Boltzman概率相應增加。即在相同模擬時間下，隨著kT的增大，所選格點被賦予新取向度值后引起晶界能增加(ΔE＞0)，晶界增多的模擬現象更容易發生，而發生格點改變取向度值后引起晶界能降低(ΔE≤0)這一事件的概率始終為 1，最終導致出現晶粒長大速率隨模擬溫度的升高而減慢這一與實際晶粒長大規律不符的模擬結果。在實際晶粒長大過程中，晶界處的物質須先克服一定能壘(G)后才能躍遷至新狀態，進而實現晶界遷移。但這一因素在原有晶粒長大MC模擬方法中并未體現。為此，本研究提出如下改進：

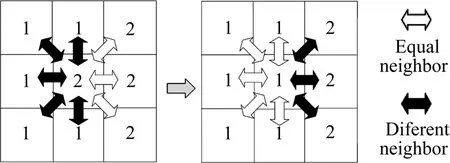
圖2 大多數MC模擬晶粒長大過程中物質狀態躍遷的模擬示意圖Fig.2 Schematic of mass status transition simulation used in previous MC method to simulate grain growth

1) 將模擬對象離散成n×n的四方格點，每個格點隨機賦予某一整數型取向度值 Q(1≤Q≤Qmax)，由此完成模擬對象初始化，本研究中n=200，Qmax=160。

2) 隨機選取任一處于晶界處的格點 i(即被選格點 i周圍有取向度不同的相鄰格點)，其取向度值為Qi，然后將每個相鄰格點的取向度值Qj(Qi≠ Qj)隨機逐一嘗試賦予被選格點 i，并根據式(4)計算相應的晶界能變化ΔE，進而給出引起晶界能降幅最大(ΔE≤0)的取向度值Qjj。若將每個相鄰格點的取向度值賦予被選格點i后，均引起晶界能增大(ΔE＞0)，則選取引起晶界能升幅最小的取向度值Qjj；若有多個取向度值賦予被選格點i后均引起晶界能降幅最大或者升幅最小，則從中隨機選取。這種“擇優轉換”的處理方式考慮了體系能量降低的最大程度是體系狀態優先變化的動力，并促使晶界朝其曲率中心移動，同時也可有效提高模擬效率[6]。

3) 根據下式給出是否賦予被選格點i新取向度值Qjj的概率(P)，然后在(0, 1)產生一個隨機數W，當P≥W時，賦予格點i新取向度值Qjj，否則，仍保持原有取向度值。式中：G為通過改變被選格點取向度值來模擬物質躍遷時所需克服的激活能壘。

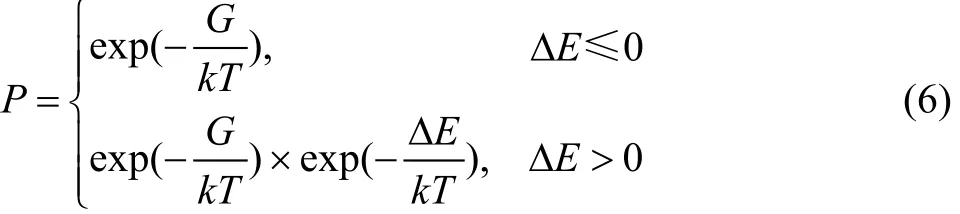
在式(6)給出的躍遷概率計算方法中，同時考慮了物質躍遷需克服一定能壘以及躍遷前、后的晶界能狀態這兩種因素，并且也能夠模擬給出物質有可能通過能量起伏向高能態躍遷的情況，因此物理意義更為明確。

對所有格點遍歷處理至到給定的模擬時間步后終止模擬，并給出相應的平均晶粒尺寸隨模擬時間延長的變化趨勢以及微觀結構。

2 結果與討論

2.1 特定模擬條件下的晶粒長大過程

圖3中所示為G = 1、J = 1以及kT = 1.0時，平均晶粒半徑隨模擬時間延長的變化趨勢及其擬合曲線。可見，隨著模擬時間的延長，平均晶粒半徑呈拋物線形式逐漸變長。其中，晶粒長大速率在模擬初期相對較快，并隨模擬時間的延長而逐漸趨于平緩，與實際晶粒長大過程相符。對平均晶粒尺寸隨模擬時間延長的變化趨勢進行擬合，所得擬合曲線與平均晶粒半徑數值變化之間吻合程度良好，并可得到擬合曲線的模擬長大指數為0.493，接近理論長大指數(0.5)。

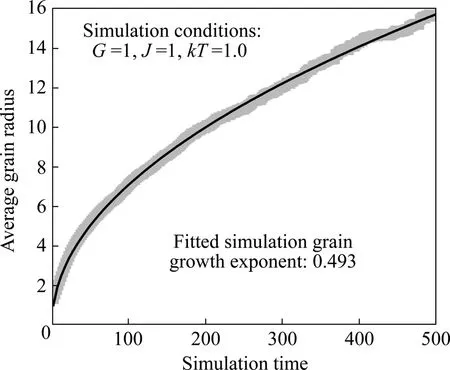
圖3 在G=1，J=1以及kT=1.0的條件下平均晶粒半徑隨模擬時間延長的變化趨勢及擬合曲線Fig.3 Change tendency and fitted curve of average grain radius with extending simulation time under conditions of G=1,J=1, and kT=1.0

圖4所示為晶粒長大微觀結構隨模擬時間延長的演變過程的模擬結果。可見，隨著模擬時間的延長，小晶粒逐漸變小，直至在晶界處消失，而大晶粒則通過吞噬周圍小晶粒逐漸長大，并具有5～7條平直晶界，最終引起晶粒總數量減少，晶粒平均尺寸增加。另外，也可以發現，晶界在向其曲率中心移動的過程中逐漸趨于平直化，有效避免了采用元胞自動機方法模擬晶粒長大過程時容易形成鋸齒狀不平整晶界的問題[18?19]。同時，三晶界交角逐漸轉變成120?，表明晶界處界面張力隨著模擬時間的延長而逐漸達到平衡狀態。另外，圖5所示為鈮鎂酸鉛陶瓷在1 200 ℃退火4 h后的斷口顯微結構，通過對比可以發現，模擬得到的晶界分布拓撲特征與實驗觀察結果較為一致。

圖4 在 G = 1，J = 1和 kT = 1模擬條件下歷經不同模擬時間后得到的模擬晶粒顯微組織: (a) tMCS=120; (b) tMCS=240;(c) tMCS=360; (d) tMCS=480Fig.4 Development of simulation microstructure with extending simulation time under conditions of G = 1, J = 1 and kT = 1.0:(a) tMCS= 120; (b) tMCS=240; (c) tMCS=360; (d) tMCS=480

圖6所示為經歷不同模擬時間后的相對晶粒尺寸的分布情況。由圖6可看出，不同模擬時間下所得到的相對晶粒尺寸均呈對數正態分布；進一步擬合得到的相對晶粒尺寸分布曲線也基本相同，即具有時間不變性。另外，也沒有出現特別粗大的晶粒，最大晶粒尺寸約為平均晶粒尺寸的2.5倍。因此，可以認為本研究采用的改進MC方法可模擬得到較為理想的正常晶粒長大過程。

圖5 鈮鎂酸鉛陶瓷在1 200 ℃退火4 h后的斷口顯微結構Fig.5 Fracture microstructure of lead magnesium niobate after being annealed at 1 200 ℃ for 4 h

2.2 不同模擬溫度下的晶粒長大過程

圖7所示為G = 1和J = 1時，平均晶粒半徑在不同kT隨模擬時間延長的變化趨勢和擬合曲線。由圖7可見，隨著模擬溫度的升高，晶粒長大速度呈加快趨勢，無需重新構建溫度—時間對應關系就能夠較好地修正原有MC模擬方法中出現晶粒長大速率隨溫度升高而減慢這一與實際晶粒長大規律不符的模擬現象。另外，在不同模擬溫度下，平均晶粒尺寸也均隨模擬時間的延長而呈拋物線形式增長，擬合后可得到模擬晶粒長大指數分布在 0.478～0.493的范圍內，均與理論長大指數(0.5)較為接近。

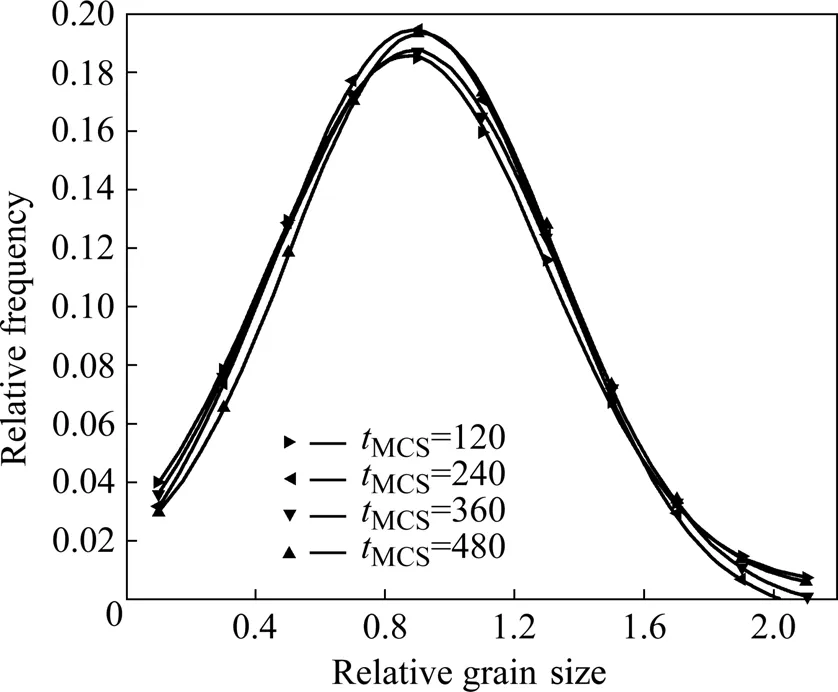
圖6 G = 1，J = 1以及kT = 1.0時經歷不同模擬時間后的相對晶粒尺寸分布情況Fig.6 Relative grain size distribution after simulation for different times under conditions of G = 1, J = 1 and kT = 1.0

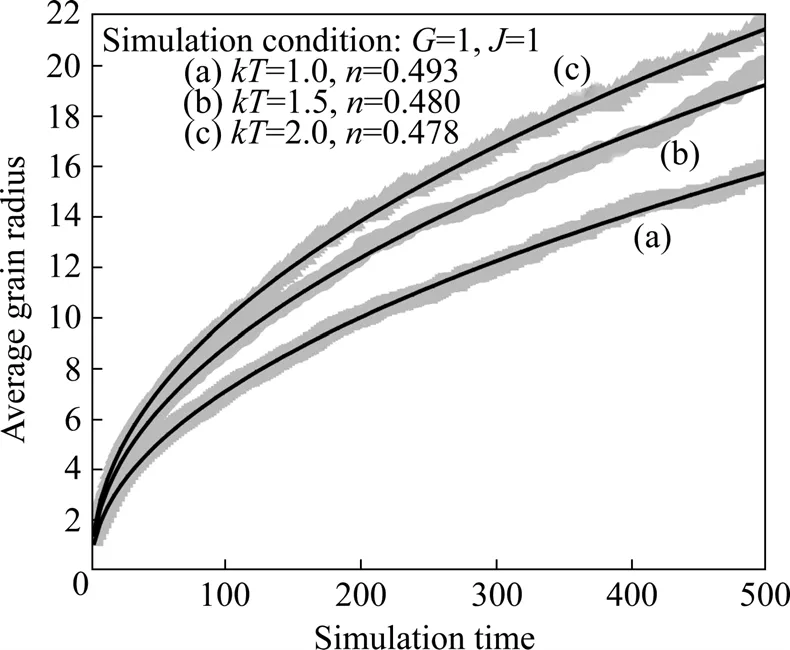
圖7 G = 1，J = 1，kT = 1.0、1.5和2.0時平均晶粒半徑隨模擬時間延長的變化趨勢和擬合曲線Fig.7 Change tendencies and fitted curves of average grain radius with extending simulation times under conditions of G = 1, J = 1, kT = 1.0 (a), 1.5 (b) and 2.0 (c)

圖8 G = 1，kT =1.0、1.5、2.0時不同模擬時間下的微觀結構Fig.8 Simulation of microstructures at different extending simulation times under condition of G = 1: (a) kT =1.0, tMCS=240;(b) kT =1.0, tMCS=480; (c) kT =1.5, tMCS=240; (d) kT =1.5, tMCS=480; (e) kT =2.0, tMCS=240; (f) kT =2.0, tMCS=480

2.3 不同激活能壘狀態下的晶粒長大過程

圖9所示為在J=1，kT=1時平均晶粒半徑隨模擬時間延長的變化趨勢和擬合曲線。由圖9可見，在模擬時間相同時，平均晶粒半徑隨著激活能壘(G)的增加而逐漸減小。對平均晶粒半徑數據進行擬合，可得到不同激活能壘狀態(G)下的模擬晶粒長大指數在0.472～0.493的范圍內。

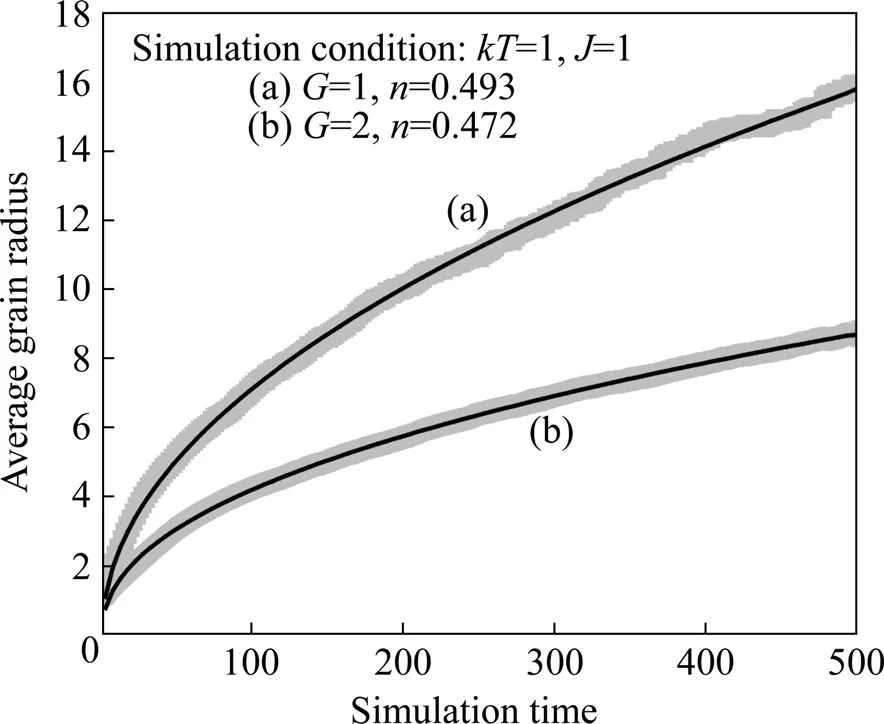
圖9 平均晶粒半徑隨模擬時間延長的變化趨勢和擬合曲線Fig.9 Change tendency and fitted curve of average grain radius with extending simulation times

圖10 kT = 1時不同模擬時間下的微觀結構的模擬結果Fig.10 Simulation of microstructure at different extending simulation times under condition of kT=1: (a) G=1, tMCS=240; (b) G=1,tMCS=480; (c) G=2, tMCS=240; (d) G=2, tMCS=480

圖10所示為J=1，kT = 1時，晶粒長大微觀結構隨模擬時間延長的演變過程。從10可看出，在模擬溫度和時間條件相同時，隨著激活能壘狀態(G)的增加，物質躍遷至相鄰其他晶粒并引起晶界遷移也變得更困難，并最終導致晶粒長大速率減慢，在模擬所得微觀結構上表現為晶粒數量相應增加，晶粒尺寸逐漸減小。

3 結論

1) 在各種模擬條件下得到的模擬晶粒長大指數在 0.472～0.493的范圍內，接近理論晶粒長大指數(0.5)。在模擬所得的微觀結構中，小晶粒隨模擬時間的延長逐漸變小，直至在晶界處消失，大晶粒通過吞噬周圍小晶粒逐漸長大，晶界向其曲率中心移動并趨于平直化，三晶界交角逐漸轉變成 120?。通過改進MC方法可以模擬得到與晶粒長大動力學相關理論和實驗現象符合較好的晶粒形貌演變過程和晶界分布拓撲特征。

2) 在躍遷概率計算中引入躍遷能壘因素，可將物質在晶界處的躍遷概率與模擬溫度直接關聯，即躍遷概率隨模擬溫度的升高而增加，進而能夠模擬得到晶粒長大速率隨模擬溫度的升高而加快的模擬結果。另外，通過增加躍遷能壘，使物質躍遷至相鄰其他晶粒并引起晶界遷移的概率降低，因此可以給出晶粒長大速率相應減慢的模擬結果。改變模擬溫度和能壘等模擬條件后，相應得到的晶粒長大速率變化趨勢與實際晶粒長大規律較為一致。

REFERENCES

[1] MORON C, MORA M, GARCIA A. Computer simulation of grain growth kinetic[J]. Journal of Magnetism and Magnetic Materials, 2000, 215/216: 153?155.

紫趾綜合征的確診需作受累器官的組織學樣本檢查，可在直徑為100μm～200μm的小動脈血管的管腔內見到膽固醇晶體，鏡下可見膽固醇晶體溶解并出現針狀裂縫[4]。

[2] BATTAILE C C. The kinetic Monte Carlo method: Foundation,implementation, and application[J]. Computer Methods in Applied Mechanics and Engineering, 2008, 197: 3386?3398.

[3] 魏承煬, 高英俊, 張麗娜. 晶粒長大的 Monte Carlo模擬方法—遞歸統計法測定晶粒度[J]. 中國有色金屬學報, 2008,18(1): 132?137.WEI Cheng-yang, GAO Ying-jun, ZHANG Li-na. Monte Carlo simulation of grain growth—Recursive statistics method of grain size[J]. The Chinese Journal of Nonferrous Metals, 2008, 18(1):132?137.

[4] HUANG C M, JOANNE C L, PATNAIK B S V,JAYAGANTHAN R. Monte Carlo simulation of grain growth in polycrystalline materials[J]. Applied Surface Science, 2006, 252:3397?4002.

[5] ZHOU Ming, LI Shi-chen, ZHENG Zi-qiao, YANG Pei-yong.Kinetics Monte Carlo simulation of microalloying effect in Al-Ag alloys[J]. Transactions of Nonferrous Metals Society of China, 2007, 17(3): 461?467.

[6] 張繼祥, 關小軍, 孫 勝. 一種改進的晶粒長大 Monte Carlo模擬方法[J]. 金屬學報, 2004, 40(5): 457?461.ZHANG Ji-xiang, GUAN Xiao-jun, SUN Sheng. A modified Monte Carlo method in grain growth simulation[J]. Acta Metallurgica Sinica, 2004, 40(5): 457?461.

[7] YU Q, ESCHE S K. A Monte Carlo algorithm for single phase normal grain growth with improved accuracy and efficiency[J].Computational Materials Science, 2003, 27: 259?270.

[8] 葉日晴, 趙建華, 何陵輝. 退火過程中晶粒長大的二維計算機模擬[J]. 無機材料學報, 2001, 16(1): 122?128.YE Ri-qing, ZHAO Jian-hua, HE Ling-hui. Computer simulation of grain growth in two dimensions in annealing process[J].Journal of Inorganic Materials, 2001, 16(1): 122?128.

[9] 陳健美, 周卓夫, 唐建國, 張新明. 一種考慮晶界能各向異性模擬晶粒長大的Monte Carlo方法[J]. 材料導報, 2003, 17(8):77?79.CHEN Jian-mei, ZHOU Zhuo-fu, TANG Jian-guo, ZHANG Xin-ming. A Monte Carlo simulation of grain growth with grain boundary energy anisotropy considered[J]. Materials Review,2003, 17(8): 77?79.

[10] OGIBAYSHI S. Monte Carlo simulation of grain growth taking into account the influence temperature[J]. ISIJ International,2008, 48(3): 368?376.

[11] RADHAKRISHNAN B, ZACHARIA T. Monte Carlo simulation of grain boundary pinning in the weld heat-affected zone[J].Metallurgical and Materials Transactions A, 1995, 26(8):2123?2130.

[12] RADHAKRISHNAN B, ZACHARIA T. Simulation of curvature-driven grain growth by using a modified Monte Carlo algorithm[J]. Metallurgical and Materials Transactions A, 1995,26(1): 168?180.

[13] GAO J H, THOMPSON R G. Real time-temperature models for Monte Carlo simulations of normal grain growth[J]. Acta Materialia, 1996, 44: 4565?4570.

[14] GEIGER J, ROOSZ A, BARKOCZY P. Simulation of grain coarsening in two dimensions by cellular automaton[J]. Acta Materialia, 2001, 49: 623?629.

[15] BINDER K. Methods in statistical physics[M]. Heidelberg:Springer, 1986.

[16] 劉祖耀, 李世晨, 鄭子樵, 陳大欽, 李 劍. 正常晶粒長大的計算機模擬(Ⅰ)—晶粒長大動力學躍遷概率的改進[J]. 中國有色金屬學報, 2003, 13(6): 1357?1360.

LIU Zu-yao, LI Shi-chen, ZHENG Zi-qiao, CHEN Da-qin, LI Jian. Computer simulation of grain growth (Ⅰ)—Modified transition probability[J]. The Chinese Journal of Nonferrous Metals, 2003, 13(6): 1357?1360.

[17] 王海東, 張 海, 李海亮, 湯育才. 焙燒過程晶粒長大的

Monte Carlo模擬[J]. 中國有色金屬學報, 2007, 17(6):990?996.

WANG Hai-dong, ZHANG Hai, LI Hai-liang, TANG Yu-cai.Monte Carlo simulation of grain growth in calcination process[J].The Chinese Journal of Nonferrous Metals, 2007, 17(6):990?996.

[18] 麻曉飛, 關小軍, 劉云騰, 申孝民, 王麗君, 宋述同, 曾慶凱.基于改進轉變規則的晶粒長大 CA模型[J]. 中國有色金屬學報, 2008, 18 (1): 138?144.MA Xiao-fei, GUAN Xiao-jun, LIU Yun-teng, SHEN Xiao-min,WANG Li-jun, SONG Shu-tong, ZENG Qing-kai. Cellular automaton model for grain growth based on modified transition rule[J]. The Chinese Journal of Nonferrous Metals, 2008, 18(1):138?144.

[19] HE Y Z, DING H L, LIU L F, SHIN K. Computer simulation of 2D grain growth using a cellular automata model based on the lowest energy principle[J]. Mater Sci Eng A, 2006, 429:236?246.

(編輯 楊 華)

Modified Monte Carlo simulation of normal grain growth considering energy barrier for mass transition

LIU Jian-yuan, ZHANG Xiao-yong, ZHOU Ke-chao
(State Key laboratory of Powder Metallurgy, Central South University, Changsha 410083, China)

TG 111; TP 391.7

A

1004-0609(2010)05-0961-08

國家重點基礎研究發展計劃資助項目(2005CB623703)；中南大學博士后科學基金資助項目(2009年)

2009-07-15；

2009-12-17

張曉泳，博士；電話：0731-88830464；E-mail: zhangxiaoyong@mail.csu.edu.cn