單位四元素法在激光點云坐標轉換中的應用

滕志遠，張愛武

(首都師范大學資源環境與旅游學院三維信息獲取與應用教育部重點實驗，北京100048)

單位四元素法在激光點云坐標轉換中的應用

滕志遠，張愛武

(首都師范大學資源環境與旅游學院三維信息獲取與應用教育部重點實驗，北京100048)

將點云配準過程中的單位四元素法應用于坐標轉換，提出一種在求解坐標轉換過程中將旋轉矩陣和平移向量轉化為求解多元函數極小值的方法，直接解出坐標轉換的旋轉矩陣和平移向量。與目前常用的一些方法相比，具有適應大旋角、不受平移參數影響、計算簡便快速、便于程序實現等優點。最后驗證該方法的精度，并用實測數據檢驗其可行性。

坐標轉換;七參數;單位四元素法

一、引 言

隨著測量技術的發展，三維激光掃描的應用越來越廣泛。三維激光掃描儀受外界環境影響小，能夠快速、連續地獲取數據，具有精度高、適應性強、應用廣泛、操作簡便等諸多優點。目前，三維激光掃描技術已在工程測量、地形測量、交通現場勘測、橋梁變形監測、古建筑和文物保護、數字城市等多個領域得到應用，取得了很好的效果［1］。

激光掃描儀獲取的數據所采用的坐標系統是它自己定義的局部三維直角坐標系，而不是各種實際中廣泛采用的坐標系，如1954北京坐標系［1］。而且在不同的站點，掃描儀的局部坐標系也是不同的。這樣既造成各站點的點云需要配準［2］，又使其應用范圍受到限制。如果能將點云坐標轉換為實際中廣泛應用的坐標，既能實現點云的配準，又能擴大點云的應用范圍。本文提出了一種將三維激光掃描儀的點云數據從其局部坐標系轉換到其他三維坐標系的方法。

二、轉換模型

傳統的三維坐標轉換方法，使用的是線性化的布爾沙模型［3］。在該模型中，需要求解3個旋轉角度參數，3個平移參數，1個尺度參數，共7個參數［4］。也稱為七參數法。轉換公式如下

其中XT=［X Y Z］T，為轉換后坐標;ΔX=［Δx Δy Δz］T，為平移向量，X=［x y z］T，為待轉換坐標;α、β、θ分別為X、Y、Z軸的旋轉角度，K為尺度參數。

如果7個參數已知，即可按照布爾莎模型公式，實現坐標的轉換。但在實際應用中，這7個參數是未知的，可如果知道3個重合點［5］就可以用最小二乘法擬合出七參數。擬合七參數的過程一般是對旋轉矩陣進行線性化后再計算七參數，但這種方法只能針對微小旋轉角的情況。當旋轉角度較大時，會產生較大的誤差，損害坐標轉換精度［6］。

為能更精確地求解七參數，科技工作者提出很多方法。如陳宇提出了非線性最小二乘的方法求解七參數，解決了大旋角情況下七參數求解［6］問題;陸玨等提出了基于總體最小二乘的方法求解七參數［7］;這些方法都是基于最小二乘擬合的思想，原理比較復雜。

本文借鑒了點云配準中的思想，將配準過程中單位四元素方法應用于坐標轉換。

三、單位四元素法

配準的過程是將不同站點點云統一到同一個坐標系下的過程。因而點云配準的過程其實也是點云的三維坐標轉換的過程。

單位四元素法的思想［8］如下：

若目標點集A對應于參考點集X，對應點集滿足：兩個點集中點的個數相等，點集中的點要一一對應。設旋轉變換向量為單位四元數

可得到3×3旋轉矩陣R(qR)。設平移變換向量為

可得完全坐標變換向量q=［qR|qT］。則求對應點集間的最佳坐標變換向量問題可轉化為q，即使得函數

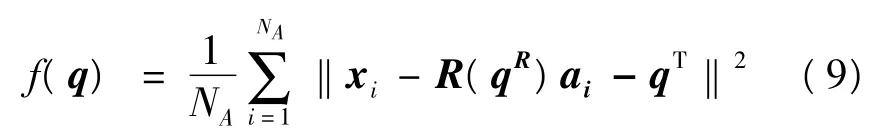
最小化的問題。

在單位四元素法中，至少需要知道3對一一對應點的坐標。

算法過程［2］如下：

1)分別求重心：原始點重心為

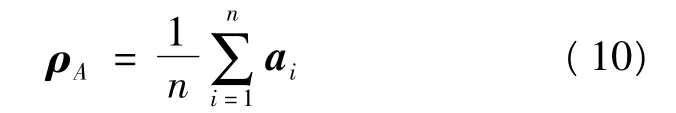
轉換后點重心為

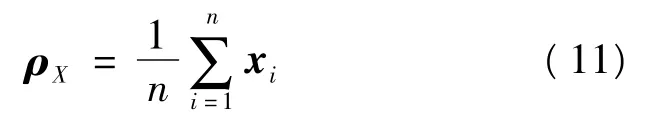
其中，n代表有n對對應點，ai、xi為帶有x、y、z坐標的點。

2)構造協方差矩陣為

3)構造4×4矩陣為

其中，tr(R(c))是矩陣R(c)的跡;I3是單位3×3單位矩陣;Δ為

其中

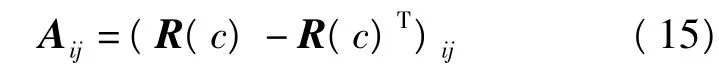
4)計算4×4矩陣R(q)的特征值和特征向量，其中最大特征值對應的特征向量即為單位四元數［q0q1q2q3］T。

5)計算旋轉矩陣為

其中，R11=q20+q21－q22－q23;R12=2(q1q2－q0q3);

R13=2(q1q3+q0q2);R21=2(q1q2+q0q3);

R22=q20－q21+q22－q23;R23=2(q2q3－q0q1);

R31=2(q1q3－q0q2);R32=2(q2q3+q0q1);

R33=q20－q21－q22+q23。

6)計算平移矩陣為

至此，計算出了旋轉矩陣和平移向量，即可實現坐標轉換。

四、測試試驗

本文選取6個點，其中3個點既有在掃描儀下的坐標，又有在轉換后坐標系下的坐標。這3個點是用來求旋轉矩陣和平移向量的。另外3個點則已知在掃描儀下的坐標。

由于是直角坐標轉換，設定尺度參數k=0，1～3號點原始坐標分別為：(32.503，163.608，0.029)，(31.534，167.955，－1.164)，(25.723，169.838，5.343)。

4～6號點原始坐標分別為：(72.356，163.140，1.948)，(65.148，175.564，12.566)，(85.720，155.195，20.232)。

表1是模擬測試試驗的結果。表1中的理論值是用七參數轉換公式，將4～6點坐標和參數代入七參數轉換公式算出的值。轉換值是4～6號點的原值代入單位四元素法算出的旋轉矩陣和平移向量得出的值。此處的旋轉矩陣和平移向量是利用1～3號點原坐標值和經七參數轉換后的坐標值算出。

如表1所示，在第一組和第二組中，平移向量參數都是確定的，兩組數據分別試驗了在不同旋角情況下坐標的轉換精度。由理論值和轉換值的對比可以看出，不論是大旋角還是小旋角，坐標轉換的誤差都很小，最大的誤差也在10－6數量級，可見本文算法在旋角很大的情況下，也有很高的轉換精度。

第一組和第三組同樣有相同的平移參數，只是三個坐標軸旋角值做了對調。由表中數據可以看出，本文算法對各個坐標軸的旋角大小無特殊要求，不論旋角是大還是小，算法均有很高的轉換精度。在第一組和第四組中，有相同旋轉參數，不同的平移參數。這種情況下，誤差仍然很小，與前面的誤差相比沒有大的變化，說明平移參數的大小對算法幾乎沒影響。將第二、三、四組的數據進行對比，在不同的旋角和不同的平移參數下，理論值和轉換值的誤差依然在10－6數量級。

表1 測試試驗

綜合以上的數據對比可以得出，本文算法在大旋角的情況下依然適用，且保持了很高的精度。旋角的大小和平移向量的大小對算法的精度幾乎無影響。

本文的算法編程實現簡單易行，運算快速。在CPU為奔騰4，主頻為3.0 GHz，內存512 MB的硬件條件下，用VC 6.0編譯，實現741 389個點的轉換并將結果輸出到磁盤上，用時22 s，而實現59 379個的點轉換并輸出到磁盤僅用時約1 s。

五、實測數據檢驗

為檢測實際效果，我們選取了一組實測數據用來檢驗算法。實測數據是將一段公路分為兩個站點進行掃描。在每一個站點的掃描前，先放置五個靶標。靶標由于反射率較高，在后處理軟件中容易識別，并取得該處靶標在掃描儀坐標系下的坐標。每一站掃描完畢，用GPS測出靶標的全局坐標(這里將全局坐標轉換為1954北京坐標系)。這樣在每站點云數據上，就至少有3對點可用來轉換坐標系。

如圖1～圖2所示的是采用本文的算法轉換后的坐標點的圖像。圖中深灰色的是一站數據，淺灰色的是另一站數據。為了突出顯示邊緣，前期對獲取的未轉換的數據進行了裁剪處理。裁剪處理過的點云數據不會影響轉換的精度。

由圖1可以看出，淺灰色點正確地處在深灰色點的缺口處，兩站數據正確地拼接在一起，形成了完整的路面。說明轉換后的點具有正確的坐標值。

圖1 轉換完的兩站數據

圖2是局部放大效果。由圖中的粗線條可以看出，兩站數據拼接的效果很好，說明本文算法轉換的坐標精度是較高的。

圖2 拼接處的放大效果

隨著三維激光掃描技術應用范圍的日益擴大，傳統的逐站點配準點云數據的方法由于需要人工手動選點，效率低，且精度不能保證，故而難以適應多站點、大數據量的配準情況。而采用本文提出的坐標轉換方法，既能實現點云的快速配準，又能保證精度，而且可以轉換成1954北京坐標等應用范圍比較廣泛的坐標，也擴大了三維激光點云在實際中的應用。

六、結束語

七參數線性模型無法適用于旋角較大的情況。而本文提出的算法在大旋角的情況下仍然有很高的精度，受平移參數的影響也很小。算法實現快速，在掃描密度不高的情況下能實現實時轉換。本算法較適合應用于將激光掃描儀數據進行三維坐標轉換的情況。

［1］ 楊偉，劉春，劉大杰.激光掃描數據三維坐標轉換的精度分析［J］.工程勘察，2004(3)：61-63.

［2］ 戴靜蘭，陳志楊，葉修梓.ICP算法在點云配準中的應用［J］.中國圖象圖形學報，2007，12(3)：517-521.

［3］ 盧忠，歸友龍，劉勇.基于總體最小二乘法的三維坐標轉換參數解算［J］.山西建筑，2009，35(36)：359-360.

［4］ 張宏.布爾莎-沃爾夫轉換模型的幾何證明［J］.測繪與空間地理信息，2006，29(2)：46-51.

［5］ 柯金樸.空間三維坐標轉換原理及實現［J］.江西測繪，2008(3)：16-20.

［6］ 陳宇，白征東.基于非線性最小二乘算法的空間坐標轉換［J］.大地測量與地球動力學，2010(2)：129-132.

［7］ 陸玨，陳義，鄭波.總體最小二乘方法在三維坐標轉換中的應用［J］.大地測量與地球動力學，2008，28(5)：77-81.

［8］ BESL P J，MCKAY N D.A Method for Registration of 3D Shapes［J］.IEEE Transactions on Pattern Analysis and Machine Intelligence，1992，14(2)：239-256.

Application of Unit Four Elements Method to Laser Point Cloud Coordinate Transformation

TENG Zhiyuan，ZHANG Aiwu

0494-0911(2010)11-0007-04

P237

B

2010-07-13

滕志遠(1984—)，男，山東威海人，碩士生，主要研究方向為三維信息獲取與應用。