強干擾下跳頻信號的提取

張 珊，吳 瑛，劉元寧2,陳秋華

(1.解放軍信息工程大學 信息工程學院，鄭州 450002；2.中國科技大學，合肥 230026)

1 引 言

跳頻技術是一種擴頻通信技術，它具有較好的抗干擾性和低截獲性。作為非合作方，當強干擾存在時，要統計跳頻信號的參數就更加困難。

時頻分析能夠反映跳頻信號在時間-頻率平面上的分布情況，目前常用的方法[1-2]包括短時傅里葉變換(STFT)、小波變換、二次時頻表示等。但二次時頻表示由于是非線性變換，不可避免地會導致交叉項的出現，而且運算復雜，應用受到限制。短時傅里葉變換是一種快速的時頻分析工具，從時頻圖中也能夠比較好地觀察出有幾個信號以及信號的特征，但是，要通過算法將這些參數提取出來，卻不是一件容易的事情。文獻[3]利用信號描述字的方法來進行參數統計。這種方法時間分辨率不高，不能解決觀察時間內同一個頻率上出現多次信號的問題，而且沒有對屬于同一個信號的多個頻率分量合并，會導致后續信號分選困難。文獻[4]提出的各種求噪聲基底的方法依賴于聶曼-皮爾遜準則，該準則要求知道一定的先驗知識，如信號的似然概率密度函數，因此該方法不適用于非合作接收。文獻[5]提出了將功率譜視為一幅圖像，采用基于圖像處理估計噪聲基底的方法。但是，該文獻沒有給出幅度軸上像素數的確定方法，而且結構元素采用了按序遞增的方式進行迭代，會出現噪聲基底估計的水平偏移，另外也沒有進一步研究估計信號的方法。

本文在短時傅里葉變換的基礎上，結合圖像處理和噪聲峰值提取的思想，改進了形態學圖像處理估計噪聲基底的算法，提出了完整的提取跳頻信號特征的方法。該方法運算簡單，能夠在強干擾存在的情況下，檢測出幅度較弱的跳頻信號。仿真實驗證明了方法的有效性。

2 信號模型

本文采用的含有噪聲和干擾的跳頻信號模型如下：

(1)

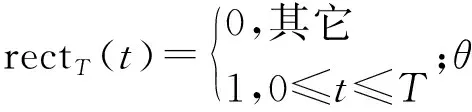
3 特征提取的方法

計算接收信號離散短時傅里葉變換：

得到信號時頻譜。短時傅里葉變換能夠體現出各段信號大概的頻率、幅度強弱、起止時間等特征。

3.1 信號檢測

要得到整個觀察時間內各個信號的參數，首先要將信號從噪聲中提取出來，然后判斷是否有信號出現、有幾個信號出現。各個信號由于源的不同、距離的遠近、路徑的不一致，功率大不相同。尤其當強信號存在時，噪聲基底將提高，如圖1所示。

如果簡單地按照某一個門限去判斷是否出現信號，將會難以實現信號與噪聲的有效分離。為此，本文首先估計噪聲基底，從原頻譜中減去噪聲基底以獲得噪聲平坦的信號頻譜，進而估計信號個數，完成信號檢測。我們采用圖像處理中的開運算來估計噪聲基底。

圖1 未經處理的信號頻譜圖Fig.1 Spectrum of primal signal

3.1.1形態學圖像處理[6]

形態學圖像處理將復雜的圖像形狀分解為不同的部分。它是基于二值圖像，依據數學形態學集合論方法發展起來的圖像處理方法。其基本思想是利用具有一定形態的結構元素去度量和提取圖像中的對應形狀，以達到對圖像分析和識別的目的。噪聲基底估計主要基于兩種運算——腐蝕和膨脹[6]。

(1) 腐蝕

集合A被集合B腐蝕，表示為AΘB：

AΘB={x:B+x?A}

(2)

式中，B+x表示將集合B平移距離x。如果原點在結構元素內部，腐蝕具有收縮圖像的功能。

(2) 膨脹

集合A被集合B膨脹，表示為A⊕B：

A⊕B=[AcΘ(-B)]c

(3)

式中，Ac表示將集合A的補集，-B為B旋轉180°。如果原點在結構元素內部，膨脹具有擴大圖像的功能。

(3)開運算

先腐蝕后膨脹的一次運算即為一次開運算。利用結構元素B對圖像A進行開運算，用符號A°B表示：

A°B=(AΘB)⊕B

(4)

3.1.2利用形態學圖像處理技術估計噪聲基底

文獻[5]給出了一種利用形態學技術估計噪聲基底，得到具有平坦噪聲的信號功率譜的方法。算法流程圖如圖2所示。該方法在信號實時處理中存在一定的問題，經過仿真實驗，我們對該算法進行了如下三方面的改進。

圖2 估計噪聲基底的流程圖Fig.2 Flow chart of noise floor estimation

(1) 用頻譜代替功率譜

考慮到功率譜是對頻譜求平方，會拉大強干擾和弱信號之間的幅度距離，噪聲算法收斂減慢，本文均采用頻譜代替功率譜，對信號提取結果沒有任何影響。

(2) 幅度軸上像素數Num的選定

由于幅度取值是連續的，如果按照每個值就代表一個像素，將會導致運算量大增。如果以強干擾作為參考，在相同的像素數下，干擾越強，則每個像素對應的幅度范圍越大，若信噪比比較低，容易將信號與噪聲劃分為同一個像素， 不能適應信噪比的變化，因此不適合用強干擾作參考。考慮到信號并不是在每個頻段都存在的，在沒有信號的頻段(如圖3中歸一化頻率為0～0.1、0.15～0.2的頻段)內的最大值反映了噪聲幅度最大值的一般水平，以此作為劃分像素數的參考，可以適應信噪比的變化。因此，本文提出采用如下方法確定像素數。

信號FFT變換的模值記為y(i)，i=1,2，3，…,Nfft,Nfft為FFT點數的一半(FFT變換具有對稱性，因此可以只考慮前半段)。將y(i)劃分為多段，每段長度設為N，求每段內的最大值ymax(i)，所有最大值的最小值就是噪聲幅度最大值ynoise的一般水平，即：

(5)

ynoise=min(ymax(i))

(6)

式中，m為滿足mN≤Nfft的最大整數。則幅度軸上的像素數可以設為

(7)

式中，round表示取最接近的整數，α為某個比例，本文的實驗取α=1/2。

(3) 結構元素的選擇

文獻[5]在進行開運算時，結構元素的增加是采用按序遞增的方式進行的。通過仿真發現，當結構元素的大小為偶數時，原點位于中心，由于像素是離散的，中間并不代表任何像素，因此必然取偏左或偏右一個作為腐蝕膨脹的中心，這樣就會導致噪聲基底估計的水平偏移，如圖3(a)所示，如果用原頻譜直接與之相減會導致頻譜的不恰當變形。而且由于每次移動的距離無法確定，也不能通過直接搬到合適位置進行相減。考慮到多進行一次開運算與少進行一次開運算的差別并不大，本文算法只采用大小為奇數的結構元素，即結構元素按1，3，5，……順序遞增，保證了噪聲基底不發生水平偏移，如圖3(b)所示。

(a)改變結構元素遞增方式前

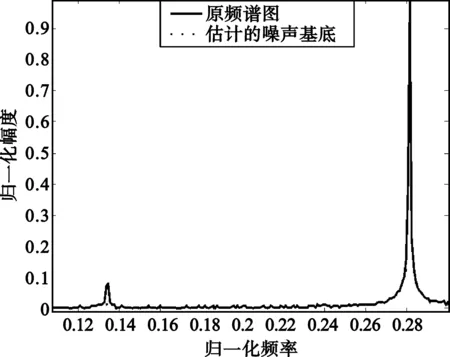
(b)改變結構元素遞增方式后

對圖1進行開運算，用原信號頻譜減去運算得到的噪聲基底，就得到了噪聲較平坦的整個觀察帶寬內的頻譜圖，如圖4所示。

圖4 利用形態學開運算后的功率譜圖Fig.4 Spetrum after the open operation of morphological image processing

通過選擇合適的門限就可以將信號從噪聲中提取出來。下面考慮門限的選擇。

3.1.3門限選擇

經過開運算后，信號頻譜中的噪聲具有平坦的分布，此時可以通過選擇單一合適門限檢測出信號。

與3.1.2節的第(1)部分類似，從圖5中可以看出沒有信號部分的最大值反映了噪聲幅度最大值的一般水平；而有信號存在的頻段，最大值必然不小于沒有信號的頻段，因此將頻譜劃分為多個頻段，選擇所有頻段的最大值的最小值，即為噪聲幅度。在此幅度基礎加上一個常數就可以作為門限，即：

threshold=ynoise+c

(7)

式中，ynoise的計算方法如式(5)、(6)，只是y(i),i=1,2,3,…,Nfft代表減去基底噪聲后的頻譜。

將幅度低于該門限的所有峰值排除掉后，統計剩下的峰值，就可以得到最終的信號個數n，這n個峰值對應的位置就是各個信號的中心頻率。

3.2 特征統計

從噪聲中得出每個時刻的信號分布后，就要統計各段信號的開始時間、結束時間和持續時間等信息，建立信號特征統計表。

(1) 由于噪聲的影響以及頻率分辨率的問題，可能同一信號在不同時間單元檢測的頻率中心位置不同；另外，對于非單頻信號，可能具有多個峰值。對這兩種情況，如果不進行處理，就會將各個峰值認為是不同的信號，造成后續信號分選的錯誤和困難增加。由于各個信號間存在一定的保護間隔，假設為Δf，比較頻率對應的列，若相鄰的頻率間隔小于Δf，則認為是同一個信號，求取它們的中心作為這個信號的中心頻率，修改對應的開始時間、結束時間和持續時間等。

(2)某些時刻幅度大的噪聲峰值可能被誤認為是信號，從而出現了虛警；也有可能某些時刻沒有檢測出信號而出現漏警，導致連續的一段信號被劃分為幾個小段。因此需要將時間間隔小于某一長度的信號刪除，然后將斷開時間小于某長度的兩段信號連接上，并修改相應持續時間等，得到最終的信號特征表。

通過最終的信號特征表，就可以根據起始時間、結束時間和持續時間等信息對信號進行檢測和分選。

4 實驗仿真

4.1 估計的信號個數隨信噪比的變化情況

仿真條件：信號頻率為5 000 Hz，干擾頻率為10 500 Hz，信干比(SIR)為-20 dB，每個信噪比下進行100次蒙特卡羅試驗，結果如圖5所示。

圖5 估計的信號個數隨信噪比的變化圖Fig.5 Signal number estimation changing with SNR

從圖5可以看出，信干比為-20 dB，信噪比高于-5 dB仍能夠較好估計信號個數，而信噪比進一步降低時，出現了漏警概率較大的情況。這是由于信噪比低時，噪聲幅度大，在進行幅度軸上的像素劃分時，每個像素對應的幅度范圍比較大，容易將信號與噪聲劃分為同一個典型幅度值，從而造成漏警。可通過減小比例因子α改善，但是α減小的同時也會導致分段數的增加，從而導致運算量增加。因此，實際中需要權衡運算量和漏警概率，進行折衷選擇。

另外，引入的常數對信號的檢測也有影響，太大則容易造成漏警，太小則造成虛警。

4.2 估計的信號個數隨最弱信號與最強信號的功率差值的變化情況

仿真條件：信號個數為2，信噪比為5 dB，每個信干比下進行100次蒙特卡羅試驗，結果如圖6所示。

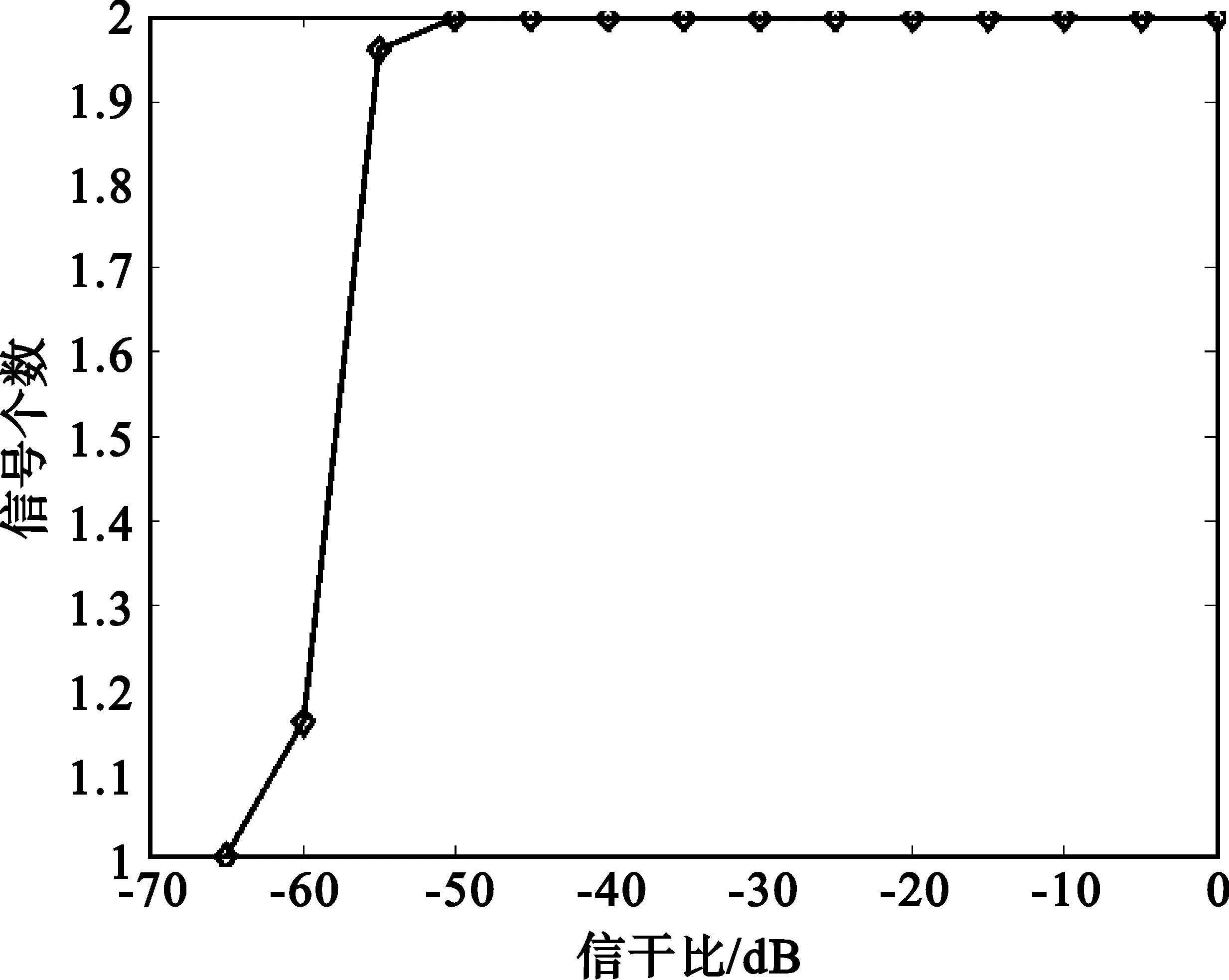
圖6 估計的信號個數隨信干比的變化圖Fig.6 Signal number estimation changing with SIR

當信干比高于-55 dB時均能夠較好地估計出信號個數，但是信干比更低時出現了漏警。這是因為隨著干擾的增強，由它引起的頻譜泄露更加嚴重，使得估計的噪聲幅度增大許多，從而劃分像素時較大范圍內的幅度將被劃分為一個像素，進而縮小了信號與噪聲之間的像素差值，容易將信號誤判為噪聲。

4.3 強干擾存在下跳頻信號的特征提取結果

仿真條件：跳頻頻率集共15個頻點，起始頻率為1 000 Hz，頻率間隔為1 000 Hz，偽隨機序列為{1，3，7，15，14，13，10，5，11，6，12，9，2，4，8}，跳速為50跳/秒，信噪比為-5 dB，干擾信號頻率為10 500 Hz，信干比為-20 dB，數據長度為15 000點。特征提取的仿真結果如表1所示。

從表1中可以看出，頻率14 026 Hz處，起始時間為189的一段信號由于觀察數據未包含完整一跳，因此持續時間比其它跳短。在頻率10 547 Hz處的信號持續時間為200，占滿整個觀察時間，可以判定為長時干擾。剩下的就是跳頻信號。根據跳頻信號的性質知，前后跳應該是首尾相接的，而且根據計算知跳頻信號每跳的持續時間應該為10個時間點。將表1按照開始時間排列，可以看出它正確反映了跳頻信號的跳變規律，但是每跳持續時間平均在15個時間點左右，相鄰兩跳重疊了5個左右時間點。這是由短時傅里葉變換的低時頻聚集特性導致的。要解決此問題，需要尋找具有更高時頻聚集特性的時頻變換方法。

表1 特征提取的結果Table 1 Characteristic pick-up result

5 小 結

本文在短時傅里葉變換的基礎上，結合圖像處理和峰值提取的思想，提出了完整的提取信號特征的方法。該方法能夠在強干擾存在的條件下，檢測出幅度較弱的跳頻信號。但是這種方法由于短時傅里葉變換本身的低時頻聚集特性，使得各段信號在時間上發生了重疊。尋找具有高時頻分辨率又不會大幅度增加運算量的時頻變換方法是下一步的研究方向。

參考文獻：

[1] 趙宏偉.基于時頻分布的跳頻信號參數檢測方法研究[D]. 西安：西北工業大學，2006.

ZHAO Hong-wei. Research of parameter detection of frequency hopping signal based on time-frequency presentation[D]. Xi′an:Northwestern Polytechnical University of China,2006.(in Chinese)

[2] Fargues Monique P,Overdyk Howard F. wavelet-based detection of frequency hopping signals[C]//Proceedings of the 31Asilomar Conference on Signal,Systems & Computers.[S.l.]:IEEE,1997:515-518．

[3] 魏宇培. 短波跳頻信號拼接解跳技術研究及其硬件實現[D]. 成都：電子科技大學，2005.

WEI Yu-pei. De-hopping of short wave frequency-hopping singal and hardware realization[D]. Chengdu:University of Electronic Science and Technology of China,2005. (in Chinese)

[4] 汪益川, 楊廷鴻,陶竹蓮,等. 基于時頻分析的噪聲去除[J]. 后勤工程學院學報,2007,23(1):49-53.

WANG Yi-chuan,YANG Ting-hong,TAO Zhu-lian,et al. The De-noising Based on Time Frequency Analysis[J]. Journal of Logistical Engineering University，2007,23(1):49-53. (in Chinese)

[5] Michael J Ready, Michael L Downey,Leo J Corbalis.Automatic Noise Floor Spectrum Estimation in the Presence of Signals [C]//Proceedings of the Thirty-First Asilomar Conference on Signals, Systems & Computers.[S.l.]:IEEE,1997: 877-881.

[6] 崔屹.圖像處理與分析—數學形態學方法及應用[M].北京：科學出版社，2000

CUI Yi. Image processing and analysis—morphological methods and applications[M]. Beijing: China Science Press，2000. (in Chinese)