船舶在隨機海浪上的穩性和傾覆研究進展

王迎光，譚家華

（上海交通大學船舶海洋與建筑工程學院，上海 200240）

1 引 言

船舶穩性是指在外力作用下，船舶發生傾斜而不致傾覆，當外力的作用消失后，仍能回復到原來平衡位置的能力，船舶的完整穩性是指船舶在未破損狀態時的穩性。船舶的完整穩性是船舶的最重要的技術性能之一。為保證所設計的船舶有良好的完整穩性，船舶工程師們通常都是要依據國際海事組織（IMO）制定的有關完整穩性衡準，即IMO的A.749（18）法案及其補充條款MSC.75（69）決議案。而IMO的A.749（18）法案主要又包含IMO在1968年的決議案A.167（ES.IV）的內容以及它在1985年的決議案A.562（14）的內容[1]。IMO基于對一些失事船舶的統計分析和船舶靜力學的原理，得出了為保證船舶完整穩性的初穩性高下限值和靜水中船舶扶正力臂曲線上幾個特定參數的下限值[1]，此即A.167（ES.IV）衡準的內容，可見A.167（ES.IV）幾乎是一個基于經驗的衡準。此后為了把“在海途中影響船舶導致傾覆或不能接受的橫傾角的外力也考慮進來”，IMO合并了已經在幾個國家實施了的氣象衡準而制定了A.562（14）決議案[3]。A.562（14）決議案雖然考慮了風傾力矩和船舶橫搖角的影響，但是橫搖角幅度的計算和風傾力矩的計算被大大地簡化了，計算中忽視了非線性的影響，而且橫傾物理模型仍然是基于假定的在靜水中的扶正力矩曲線。可見A.562（14）決議案仍然是一個半經驗的衡準。總之，現行的IMO完整穩性衡準并不是基于一個實際的物理模型，風、浪作用的隨機性，船舶運動的非線性以及各自由度運動之間的耦合效應等因素都幾乎沒被考慮進來，因而依據這些衡準設計的船舶的安全程度并不能被確切的量化[3]。同時這些衡準并不能給設計者提示應修改哪個船舶參數才能改進設計[3]。因而國際海事組織提出了完整穩性衡準長期的發展目標是應從這些約定俗成的規則（prescriptive rules）過渡到基于性能的理性規則（performance-based rational rules)[3]。即新衡準應建立在“基于第一原理分析”的基礎上[3]。

但是船舶在隨機海浪上傾覆卻是一個極其復雜的問題，雖然經過了近幾個世紀時間的研究，人們仍然缺乏對傾覆現象的完全的數學描述和透徹的物理理解[4]。至今人們在處理船舶在隨機海浪上的傾覆問題時采用的“基于第一原理”的分析方法有時域仿真、邁爾尼科夫法和首次穿越理論等。本文將結合作者研究小組的工作來對國內外這一領域內的研究進展做出綜述。

2 時域仿真

假定船寬、吃水與船長相比是小量，并且將船舶視為一無阻尼轉動振子，威廉姆-傅汝德（William Froude）推得了船舶在正弦橫浪中的橫搖運動表達式[5]，他的理論至今仍然是現代船舶在隨機海浪上傾覆研究的基礎。在十九世紀末，克雷羅夫（Alexei N.Krylov）延伸了傅汝德的上述理論，他根據波浪激勵的傅汝德克雷羅夫假定而建立了船舶六自由度振蕩運動的理論[6]。以下對基于上述思想的現代船舶運動理論作一簡要介紹。

2.1 船舶運動微分方程的建立

船舶在不規則波中的響應可被認為是船舶在對應于此特定不規則波譜范圍內所有頻率的規則波中的響應之和[7]。首先讓我們考慮一艘以定常速度U在規則正弦波中航行的船舶，船舶的航向角是任意的，在圖 1[8]中，（x,y,）z是一個對照船的平均位置而被固定的右手坐標系，z軸通過船舶的重心而垂直向上，x的方向同船舶前進的方向，坐標系原點取在未受擾動的自由表面平面內。在海面上航行的不受約束力的船舶將產生六個自由度的運動，即船舶運動可被認為是由三個平移成分（縱蕩、橫蕩和升沉）和三個轉動成分（橫搖、縱搖和首尾搖）組成。在圖1中，令在x、y和z方向上的相對于坐標原點的船舶平移位移分別為η1、η2和η3，那么 η1代表縱蕩位移，η2代表橫蕩位移，η3代表升沉位移。進一步，令相對于x、y、z軸的角位移分別為 η4、η5和 η6，那么 η4代表橫搖角，η5代表縱搖角，η6代表首尾搖角。假定船舶的振蕩運動是線性的和諧和的，則可得到六個線性的和耦合的船舶運動微分方程。利用下標記號，這六個船舶運動微分方程可被簡寫為[9]：

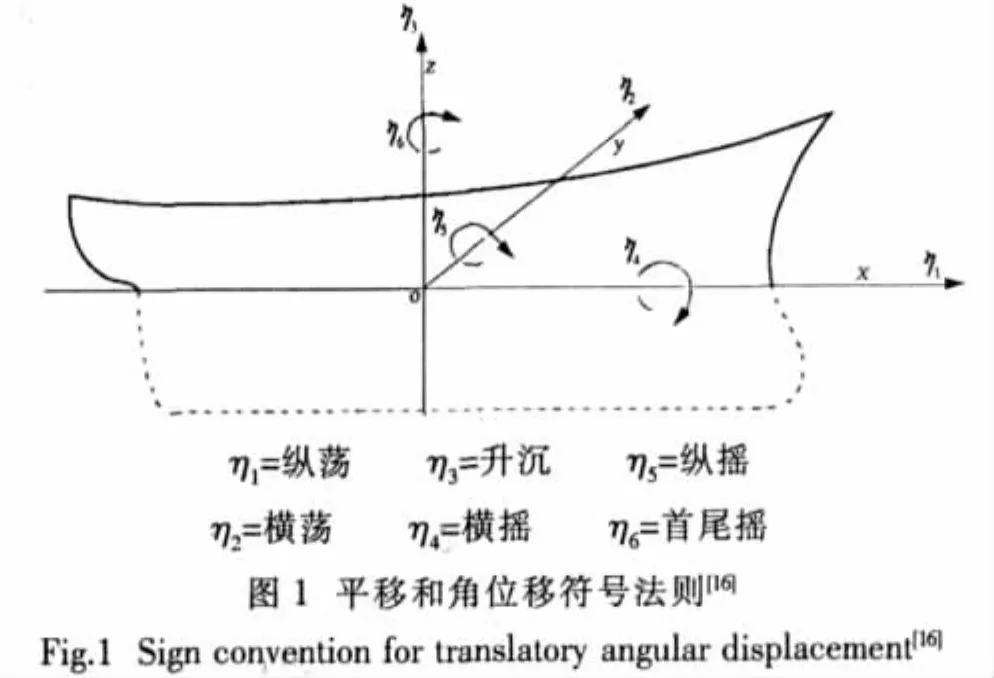
其中Mjk是船舶的廣義質量矩陣中的成分，Ajk是船舶的廣義附加質量系數矩陣中的成分，Bjk是船舶的阻尼系數矩陣中的成分，Cjk是船舶的靜水復原力系數矩陣中的成分，Fj是激勵力和力矩復數幅值，激勵力和力矩由的實部給出。F1代表縱蕩激勵力幅值，F2代表橫蕩激勵力幅值，F3代表升沉激勵力幅值，F4代表橫搖激勵力矩幅值，F5代表縱搖激勵力矩幅值，F6代表首尾搖激勵力矩幅值，以上諸力（力矩）又分別包括傅汝德-克雷羅夫力（力矩）和繞射力（力矩）兩部分。ω代表遭遇波浪頻率，這個頻率也等于響應頻率。符號（·）代表對時間求導，因而η˙k代表速度項，η¨k代表加速度項。

在上述方程（1）中，附加質量系數Ajk和阻尼系數Bjk可根據線性勢流理論求得，例如利用線性勢流理論求得的計算A44的公式為[9]：

利用線性勢流理論求得的計算B44的公式為[9]：

上述方程（2）和（3）中的積分是沿整個船長進行的。a44是船舶某一個兩維切片（在應用線性切片理論時，假定將船舶沿船長方向切成一定數目的薄片）的橫搖附加質量系數，計算這個系數的方法將在下面介紹。b44是船舶某一個兩維切片的橫搖阻尼系數，計算這個系數的方法將在下面介紹。ξ是在x方向的積分變量。是船舶最后面的一個兩維切片的橫搖附加質量系數是船舶最后面的一個兩維切片的橫搖阻尼系數代表粘性橫搖阻尼實際上是非線性的，但文獻[9]給出了其擬線性化的計算方法。

在方程（1）中，波浪激勵力或力矩也可根據線性勢流理論求得，例如利用線性勢流理論求得的計算橫搖激勵力矩幅值的公式為[9]：

其中兩維切片的傅汝德克雷羅夫“力”可按下式計算[9]:

兩維切片的繞射“力”可按下式計算[9]：

方程（4）到（6）中的數值積分是先沿切面Cx進行，再沿整個船長進行的，Cx是船舶某一個兩維切片的外輪廓圍線，dl是Cx的方向元素，ξ是在x方向的積分變量。α是波浪幅值，ρ是流體的質量密度，g是重力加速度，k 代表波數，β代表航向角（隨浪時 β=0°），N2、N3和 N4是在（y-z）平面內的兩維廣義法線，ψ4是船舶某一個兩維切片的兩維橫搖速度勢，下面將介紹求取ψ4、a44和b44的方法：

計算ψ4、a44和b44等兩維系數是船舶運動計算過程中最復雜和最耗時的，然而為了獲得有用的最終結果，精確計算這些兩維切片上的系數又是絕對必須的。數學上，計算這些兩維切片上的系數的問題被稱為混合邊界值問題，在船舶水動力學中解決混合邊界值問題的一種最常用的方法是邊界積分法。在應用邊界積分法時，先將某一船舶切片上的船舶橫剖線分成一系列直線段，然后在每一直線段上分布帶定常（但未知）強度的流體源，選擇單位源的勢函數的形式以便在自由表面和無窮遠處的邊界條件被滿足，通過滿足在每一直線段的中點上的船體邊界條件而求得未知的源強。求得了源強以后，橫搖速度勢ψ4就可被求得，那么a44和b44可根據下列公式求出[8]：

請注意上式是通過復數的實部和虛部分別相等來求解的。邊界積分法的優點是計算速度快，對船舶橫剖線近似的精度可通過多取直線段的辦法來提高，求得了ψ4、a44和b44等兩維系數以后，船舶的運動響應和穩性就可根據方程（1）到（6）求得。所謂的用時域仿真來研究船舶在隨機海浪上的穩性，即是用四階龍格—庫塔法來對微分方程（1）進行數值積分，并對求得的各響應歷經做統計處理。對一般情況下的橫穩性研究來說，這種方法可生成兩種類型的結果：達致傾覆所需的平均時間；或在一特定時間段內超過一特定橫搖角的概率。

2.2 國內外對船舶在隨機海浪上的穩性的時域仿真研究

加州大學的Paulling教授從上世紀八十年代開始進行船舶在隨機海浪上的穩性的時域仿真研究。他和其學生開發了一個數值模型來決定船舶在惡劣波浪狀況下（包括那些能導致傾覆的海況）的大幅值運動[10]。他們檢查了船舶大幅值運動方程中的各種力成分，并進行了分析來決定橫搖響應對這些力成分的變化的敏感度。McTaggart等人[11]提出了用時域仿真來決定給定海途和運營狀況下的船舶的傾覆危險的一個有效方法，最大橫搖角對波浪過程的依賴度被通過以下方法建模：將一合適的分布擬合到由中等數量的仿真得出的各最大橫搖角上。通過一驅逐艦的實例計算顯示：龔貝爾分布可很好地擬合到由不同波浪實現得到的各最大橫搖角上。De Kat等人[12]預報了船舶和近海平臺的極端運動和傾覆行為，他們仔細處理了數值建模的各個細節。De Kat等人[13]提出了一個對艦船進行傾覆概率評估的方法，他們用時域仿真得到了極端橫搖角的短期和長期統計分布。

近期王迎光等人[14-15]對用時域仿真分析海洋結構物在隨機海浪上的極端響應和穩性的原理做了詳盡的闡述：即首先為海洋結構物建立運動微分方程，并以有限數目的帶不同幅值頻率和隨機相位角的三角函數疊加來仿真隨機海浪[16-17]，接著可用四階龍格—庫塔法來對運動微分方程進行數值積分，就可獲得該海洋結構物位移響應的一個時間歷經，用同樣的方法可獲得該海洋結構物位移響應的一階導數的一個時間歷經。將該海洋結構物位移響應的時間歷經的足夠多次記錄的總體取均值可獲得結構位移響應的概率密度曲線，用同樣的方法可獲得該海洋結構物位移響應的一階導數的概率密度曲線，基于這些單個隨機變量的概率密度曲線的信息，響應值與響應值一階導數的聯合概率密度可被求得。接下來可由Rice公式求得結構系統的響應的跨越某一水準的比率（向上水準跨越率）。最后隨機激勵下海洋結構物極端響應的問題可用數學上隨機過程求極值的理論來處理[18-20]。王迎光等人[15，21]并用上述程序求得了一張力腿平臺在隨機海浪上的縱蕩響應的向上水準跨越率。

2.3 時域仿真的優缺點

用時域仿真分析船舶在隨機海浪上的穩性的原理上是十分簡明的，執行起來也很方便。而且顯見前幾節中的時域仿真的過程是一個基于“第一原理的”分析計算的過程。該方法分析的是一個現實的物理模型，它可將船舶本身的各個物理參數與船舶的完整穩性表現關聯起來，因而可使得設計者直接得到改進穩性和優化設計的具體方案。用時域仿真可方便靈活地處理復雜的非線性隨機問題，但處理在極端氣象下的極端運動的三維非線性水動力/空氣動力模型現在還沒有被擺上議事日程[3]。同時也需要國際上的合作來使時域仿真計算機軟件標準化，這一目標顯然在短時期內是難以達到的。

用時域仿真分析船舶在隨機海浪上的穩性的另一缺點是耗時巨大，王迎光[22]也用計算實例對此做了定量的說明。我們都知道在對船舶運動微分方程進行數值積分時，應該給出在0時刻的運動位移和運動速度，即給出兩個運動的初始條件，另外還要給出積分的時間域。積分的時間域是可以指定的，例如激勵力特征周期的50倍，但運動的初始條件實際上確是千變萬化的。在一般情況下的橫穩性分析時，對每一運動的初始條件都應對運動方程進行數值積分，直到船舶的橫搖角到達一預定的傾覆角。因而應對運動方程進行很多次數值積分（對應于各個不同的運動初始條件）才能得到統計上有意義的“達致傾覆所需的平均時間”或“在一特定時間段內超過一特定橫搖角的概率”。這勢必會耗費大量的計算時間。

3 邁爾尼科夫法

國內外的科研工作者為開發更高效的理性分析船舶穩性的方法做出了不懈的努力，人們基于現代的非線性隨機動力學理論，開發出了理性分析船舶動態穩性的邁爾尼科夫法（Melnikov method），并通過實船運用和船模實驗證明了邁爾尼科夫法的合理性。在一般情況下的橫穩性分析時，邁爾尼科夫法并不直接求解船舶橫搖運動的非線性隨機微分方程，取而代之的是，邁爾尼科夫法專注于研究系統的質的方面的行為（或者更精確地說，質的方面不同的行為間的轉變）。邁爾尼科夫法的一個重要分析結果是邁爾尼科夫（Melnikov）函數，有關邁爾尼可夫理論的闡述可見Guckenheimer John和 Holmes Philip[23]，Wiggins[24]以及 Moon[25]等人各自的專著。邁爾尼可夫函數可以預報在一定種類系統中的混沌的產生，在存在混沌的情況下，質的方面不同的行為的相位空間域（例如，船舶橫搖運動安全域和船舶傾覆域）可以從一個域（例如，船舶橫搖運動安全域）被傳輸到另一個域（例如船舶傾覆域）,這將導致船舶意料外傾覆的發生。以下對邁爾尼科夫法的原理和公式作一簡要介紹。

3.1 邁爾尼科夫法的原理和公式

在絕大多數情況下，船舶都是被設計成為左右對稱的,當船舶左右對稱時，縱蕩與橫搖、升沉與橫搖、縱搖與橫搖之間的一階耦合均為零。但橫蕩與橫搖、首尾搖與橫搖之間的一階耦合卻不為零。在本研究中，首尾搖與橫搖之間的耦合被假定為小量，因而只需考慮橫蕩和橫搖之間的耦合。一般來講，因為有阻尼，橫搖和橫蕩運動是不能被解耦的，但在一些特殊的情況下，例如無阻尼或帶成比例阻尼的船舶，我們可以證明在這些情況下船舶將像一個單擺一樣繞一個橫搖中心橫搖，因而橫搖運動和橫蕩運動可被解耦。當存在一般性的阻尼時，如果假定一個偽橫搖中心存在，則我們可獲得如下的帶非線性橫搖阻尼系數的單自由度橫搖運動微分方程[26]：

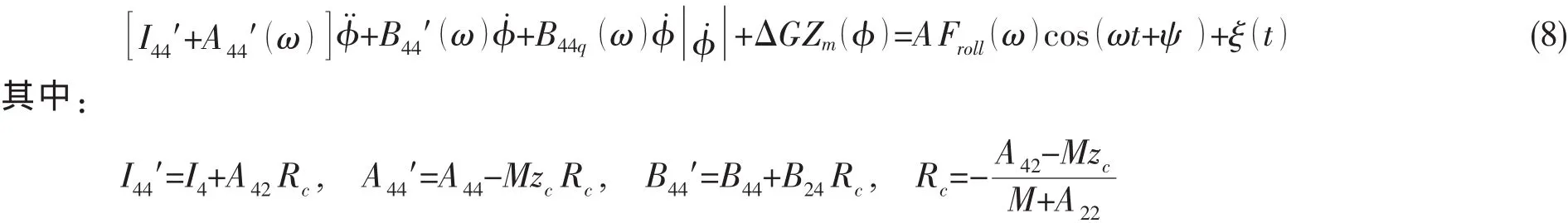
其中I4代表船舶質量對于船舶縱軸的慣量系數，A42代表由船舶的單位橫蕩位移引起的在橫搖方向上的附加質量系數，Rc是偽橫搖中心在船舶重心之上的距離。φ是橫搖角，符號（·）代表對時間求導。A44代表船舶附加質量對于船舶縱軸的慣量系數，M代表船舶質量系數，zc是船舶重心垂向高度，B44代表船舶在橫搖方向上的阻尼力矩系數，B24代表由船舶的單位橫搖角引起的在橫蕩方向上的阻尼力系數，A22代表船舶在橫蕩方向上的附加質量系數，ω代表遭遇波浪頻率，Δ是船舶的排水量，GZm（φ）是非線性橫搖復原力臂的多項式近似。A是波浪幅值，Froll（ω）是每單位波浪幅值的激勵力矩，Froll（ω）可用一些商用的水動力軟件求出。ψ是激勵力矩和入射波之間的參考相位角。ξ（t）是一個理想的、零均值和δ相關的高斯白噪聲，這個附加的高斯白噪聲近似了對外界諧和激勵力的隨機擾動。這種做法在船舶初始設計階段是允許的，此時船舶的各個詳細參數還沒有被最后確定，還沒經過詳細計算得出船舶的響應幅值算子，或者還沒有進行模型試驗得出船舶的響應幅值算子，用諧和激勵附加高斯白噪聲來近似實際的隨機波浪外激勵可快速地評價船舶的響應和穩性表現，以便提出改進方案而進入下一輪循環設計。

為研究船舶的動態穩性，一般的做法是用四階龍格—庫塔法來對微分方程（8）進行數值積分，在求得了船舶橫搖運動的響應的時間歷經以后來與靜穩性消失角或進水角 （如果進水角小于穩性消失角的話）比較。在經過很多次仿真以后，將所得到的結果進行統計分析，從而找出帶規律性的結論。但是一個沒有經驗的仿真者可能會對微分方程（8）來進行日復一日的數值積分，卻永遠也發現不了其中最重要的或最關鍵的結論。

邁爾尼科夫法能夠為船舶工程師分析船舶動態穩性提供一條新的途徑，邁爾尼科夫法是建立在現代的非線性動力學理論的基礎之上的。在用邁爾尼科夫法進行船舶動態穩性分析的過程中得到的一個重要結果是邁爾尼科夫衡準，在有些情況下，這個衡準能將船舶設計參數（船舶靜穩性臂曲線形狀和阻尼）和波浪特征參數以一個簡單的解析公式聯系起來，這將極大地提高人們理性地分析船舶動態穩性的效率。即使是在有些情況下我們得不出邁爾尼科夫函數的解析表達式，我們也可以很直截了當地用數值方法來求解此函數。為了方便地應用邁爾尼科夫分析，我們先將方程（8）寫成如下無因次形式[27]：

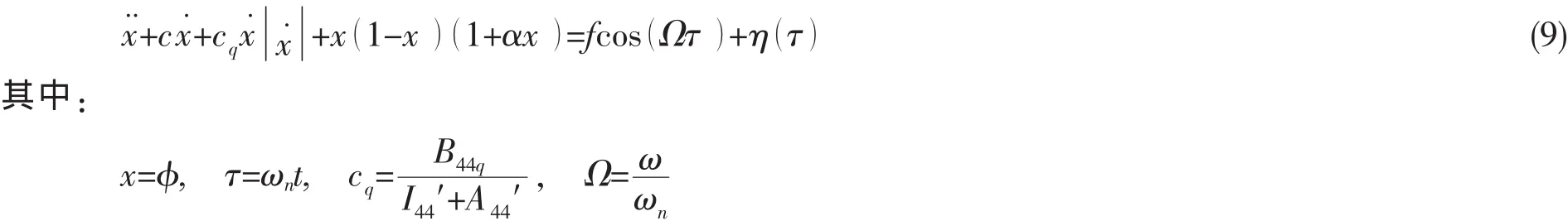
請注意在方程（9）中我們重新取了一個以船舶諧搖頻率ωn表示的比例時間τ，方程（9）中的求導是對時間τ而言的，在變換過程中我們將方程（8）兩邊同除了［I44′＋A44′（ω）］，而且非線性橫搖復原力臂取了Thompson的α-參數族復原力函數[27]。方程（9）中的c、f是在代數推導過程中得到的中間系數，〈η（τ）〉＝0，〈η（τ′）η（τ）〉＝kδ（τ′- τ） ，δ（…）是狄拉克 δ函數，k代表高斯白噪聲強度。 請注意，這里不失一般性我們取了ψ=0。用統計線性化的辦法對平方阻尼項進行等效線性化，方程（9）可被簡化為：

近期王迎光等人[28]對用邁爾尼科夫法分析船舶動態穩性的原理做了詳盡的闡述，介紹了邁爾尼科夫法對船舶意料外傾覆機理的解釋，指出為了避免船舶意料外傾覆則邁爾尼科夫函數不應該有簡單零點。如果邁爾尼科夫函數無簡單零點，穩定流形和不穩定流形將不橫向相交，異宿纏結將不會生成。因而跨越偽分界線的相位空間傳輸將不能實現，船舶意料外傾覆將不會發生，王迎光等人[28]推導得出了下述船舶在隨機激勵下大幅值混沌橫搖運動響應的邁爾尼科夫衡準，該衡準以參數f，Ω，β，α和k表示如下[28]：

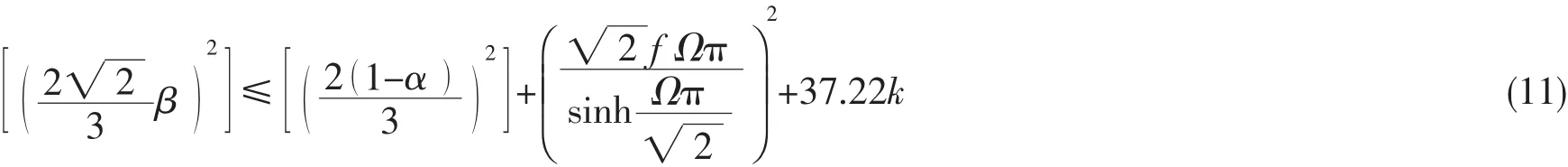
當方程（11）中的等式成立時就可獲得混沌橫搖運動的臨界面的均方值表達式。

3.2 國內外對邁爾尼科夫法分析船舶穩性的已有研究

Makoto Kan等人[29-32]的船模實驗在邁爾尼科夫法的早期發展過程中起了很大的促進作用。實驗的對象是一條135m長的集裝箱船（模型船長3.5m），實驗在日本船舶技術研究所的80m×80m的方形水池中進行，在總共763次在不規則波和規則波的運行中，發現了225次傾覆，而且發現其中25%的傾覆是與倍周期分叉（period doubling bifurcation)現象聯系的，根據非線性動力學理論，出現倍周期分叉現象是系統中產生混沌的前奏，同樣根據非線性動力學理論，邁爾尼可夫函數可以預報在一定種類系統中的混沌的產生，這即從實驗和理論上證明了用邁爾尼可夫法預報船舶傾覆行為的可行性。Makoto Kan等人[29-32]進一步也進行了極大數量的仿真來預報船舶的傾覆行為，并與邁爾尼可夫法預報的結果作了比對，同樣發現邁爾尼可夫解析分析可以被用來作為傾覆衡準（criteria for capsizing)。

Falzarano等人[33-34]用邁爾尼可夫法研究了一艘小漁船（Patti-B）的瞬態橫搖運動，這是一條傾覆過兩次的漁船，船長22.9m。它的第一次傾覆發生在靠近海岸附近，當時它被人們救起了。時隔兩年以后，它在遠離海岸處發生了第二次傾覆，永遠沉沒了。在設計過程中進行穩性計算時，發現這艘漁輪的穩性是超出了規范要求的衡準值的。這是一個典型的發生船舶意料外傾覆的例子，Falzarano等人在事后研究中認為Patti-B漁船的傾覆是與現行靜穩性衡準還沒有考慮到的一些動態效應有關的，他們在事后研究中導得了該船的橫搖運動微分方程，并根據某線性水動力軟件計算得到了該漁輪運動方程中的各水動力參數，接著通過重取一個比例時間將該船的橫搖運動微分方程化成了無因次形式的。他們接著用邁爾尼可夫法和相位空間傳輸理論對該漁輪的意料外傾覆機理做了解釋，在導得該漁輪的邁爾尼可夫衡準公式后，計算得到了導致該漁輪傾覆的臨界波浪橫搖激勵力矩值和臨界波高值。

Hsien，Shang-Rou等人[35]用一單自由度橫搖模型來研究船舶在隨機海浪中的傾覆問題。他們在分析中考慮了海浪譜，非線性復原力矩特性和非線性阻尼等幾個因素。通過邁爾尼可夫函數，相位空間面積通量和隨機振動的結合而開發了一套非線性概率法。獲得了用有義波高、波浪特征周期、阻尼和剛度系數表達的發生船舶傾覆的條件,他們在研究中證明了邁爾尼科夫解析解的有效性。Bikdash等人[36]用邁爾尼科夫法的觀點檢查了船舶橫搖平方型和立方型非線性阻尼系數之間的等效性。Lin Huan等人[26]開發了一套基于均方值的隨機邁爾尼可夫法來研究船舶在隨機激勵下的傾覆問題，但他們的運動方程中的復原力矩都是對稱型式的。

密歇根大學的船舶科研人員Jiang等人[37-38]用隨機邁爾尼可夫法（Stochastic Melnikov method）研究了船舶在隨機海浪中的強非線性橫搖運動和傾覆問題，他們考慮了船舶有初始橫傾的影響。在他們的研究中，他們應用了非線性動力系統分析的最新發展。Jiang等人[38]在未受擾動系統模型的相平面內定義了安全域和不安全域來區分本質上不同的船舶傾覆運動和非傾覆運動。當系統的解逸出安全域時就代表了傾覆的發生，Jiang等人[38]用邁爾尼科夫（Melnikov）函數和相流率的概念研究了出現這種解的概率，他們的研究顯示這些解析工具能夠提供有關船舶在一給定海況下傾覆的可靠的、有預見性的信息。Jiang等人[38]在研究中同時指出：蠻力仿真（brute force simulation,雖然字面上這樣翻譯，但并無貶義，這是學術界對仿真直截了當地處理問題的一種形象描述）只能作為理性分析方法的輔助工具，卻永遠也替代不了理性分析方法。

Chen[39-42]通過詳細的數學推演和將變量數降低，將邁爾尼可夫法成功地應用于船舶的多自由度非線性運動問題。

Thompson在其綜述文獻[27]中指出：邁爾尼可夫曲線總能很好的估計傾覆（稍微有點保守）。Scolan[43]討論了用邁爾尼可夫法研究帶高階多項式復原力矩的船舶橫搖的可行性。邁爾尼可夫法被逐漸應用于一些更復雜的橫搖數學模型，Jiang等人[44]在2000年應用邁爾尼可夫法時考慮了流體動力的記憶效果，使得所考慮的動力系統有無窮維。Spyron等人[45]對2000年以前邁爾尼可夫法的重要進展應用作了回顧。Spyrou等人[46]利用邁爾尼科夫法來評估了橫浪中一帶橫搖初始傾斜的船舶的安全性，他們獲得了表征傾覆性和將臨界波傾、橫傾量和阻尼聯系起來的閉合型關系式，在他們的研究中邁爾尼科夫公式的精確性得到了驗證。McCue[47]指出了將邁爾尼科夫法與實驗法聯合應用來處理非常規船型和高性能船舶穩性的前景。近期Spyrou[48]利用邁爾尼科夫法來研究了隨浪中船舶的非對稱縱蕩問題。

值得注意的是國內的科研人員也在將邁爾尼科夫法積極地運用到船舶穩性的研究中，例如上海交通大學的沈棟[49-50]在隨機橫浪作用下船舶傾覆概率的研究中就曾采用過邁爾尼科夫法。紀剛等人[51]運用安全池理論計算了船舶穩性，安全池在一定條件下將發生破損，此時船舶極易傾覆，他們用邁爾尼科夫法導出安全池破損的條件，以某型船舶為例，計算了該船舶安全池破損的閾值，對五個海況進行了安全性校核，并與現行規范采用的極限載荷法進行了比較，通過數值仿真繪制了各參數條件下的安全池。袁遠等人[52]用邁爾尼科夫法研究了船舶在規則波中的傾覆。袁遠等人[53]隨后用邁爾尼科夫法研究了船舶在隨機橫浪中的傾覆，他們應用非線性隨機動力系統理論，從系統穩定性的角度來分析船舶在隨機橫浪上的運動穩定性，籍此來研究隨機海浪中船舶傾覆的機理。他們的研究發現隨機動力系統的全局分岔是導致系統失穩并導致船舶傾覆的一種途徑，基于這一思路借助隨機邁爾尼科夫法，通過求取相流函數零點得到了船舶運動全局穩定性喪失時海浪條件的閾值，從而可以對船舶的抗傾覆能力做出定量的考察。金咸定等人[54]基于非線性動力學理論，以系統運動的全局分岔為出發點，來探索在規則橫浪中船舶傾覆的機理，應用邁爾尼科夫法，通過構造船舶運動的邁爾尼科夫函數來獲得導致船舶傾覆的海浪條件的閾值，從而對船舶的安全營運起到一定的指導作用。為了解決解析分析邁爾尼科夫函數的難題，他們在研究中還提出了便于工程分析應用的邁爾尼科夫函數的數值算法。唐友剛等人[55]應用邁爾尼科夫函數和相空間轉移率研究船舶在隨機波浪中的強非線性橫搖運動及其傾覆問題，分析了波浪特征頻率、特征波高、船舶非線性復原力臂以及阻尼特性對相空間轉移率的影響。以長30.7m、寬6.9m的漁船為例，采用ISSC波浪譜，在時域內計算了邁爾尼科夫函數，得到了相空間轉移率與邁爾尼科夫函數之間的關系以及有義波高對相空間轉移率的影響，他們的研究表明：隨著有義波高增大，相空間轉移率不斷增大，船舶航行的安全域迅速減小。從而揭示了相空間轉移率與船舶傾覆的內在密切聯系，為船舶的設計和穩性衡準提供了有價值的參考。劉利琴等人[56]綜述了國內采用非線性動力學理論和方法研究船舶運動的復雜動力學行為方面的進展，特別總結了在船舶非線性耦合運動、橫浪運動、縱浪上參數激勵運動和波浪上參數與波浪聯合激勵運動方面的研究現狀及取得的主要成果，介紹了船舶在隨機橫風橫浪中安全池的分析方法及采用邁爾尼科夫法研究船舶傾覆運動特性取得的進展。浦金云等人[57]系統地分析了具有淹水艙的艦船在波浪中橫搖運動時船和艙內水的能量耦合作用,根據拉格朗日方程建立了具有淹水艙的艦船橫搖運動兩自由度微分方程，并在此基礎上，用邁爾尼科夫法對某實船破損進水后的橫搖運動進行了非線性分析，驗證了所建模型的實用性，為進一步分析破損進水艦船在風浪中的橫搖運動特性提供了可行的數學模型。

3.3 應用邁爾尼可夫法時應注意的問題

我們注意到在推導邁爾尼科夫衡準公式（11）時只考慮了橫搖和橫蕩運動，這也就是說在用已有的邁爾尼科夫衡準作實例分析時只研究了船舶的橫穩性。因為所有的船舶都主要是在橫向傾覆[58]，用邁爾尼科夫分析就可以輔助處理初始設計階段大多數的船舶穩性問題。但是船舶的隨浪穩性問題目前也在引起人們的注意，用邁爾尼科夫解析分析來處理此類問題看來是有局限的[48]，因為在數學建模時要包含作用于船上的載荷的過多細節[48]。

4 首次穿越理論

4.1 國內外對用首次穿越理論分析船舶穩性的已有研究

研究船舶在隨機海浪中的穩性和傾覆問題的另一方法是利用隨機結構動力學中的首次穿越（first passage）理論。目前對于首次穿越問題只有基于馬爾科夫（Markov）隨機過程的一階問題才有解。文獻[59]的作者研究了由諧和和白噪聲聯合激勵的非線性振蕩系統的首次穿越時間。他們首先用隨機平均法將系統運動方程降階為一組伊藤（It?）隨機微分方程，接著建立了控制條件可靠性函數的后向科馬格諾夫（Kolmogorov）方程和一組控制首次穿越時間條件矩的廣義龐垂亞根（Pontryagin）方程。最后通過解帶適當的初始和邊界條件的后向Kolmogorov方程和廣義Pontryagin方程獲得了條件可靠性函數和首次穿越時間的條件概率密度和條件矩。他們用數值仿真驗證了其解析解。以上即是解決首次穿越問題的一般步驟。已故英國學者Roberts[60-64]不但對首次穿越理論的發展貢獻頗多，而且首先應用首次穿越理論來進行船舶在隨機海浪中的橫搖和傾覆研究。他[65-67]首先采用基于能量包線的隨機平均法來預報受不規則波激勵的船舶和運輸駁船的橫搖響應的平均首次穿越時間，基于能量包線的隨機平均法并不受外激勵水平高低的限制。但是應該指出文獻[65]、[66]和[67]研究的重點是開發船舶橫搖運動的隨機理論，有關船舶穩性的首次穿越理論并沒有被完整地系統地闡述出來，所提供的計算的例子也太過于簡化。近期王迎光等人[68]在Roberts的初步工作的基礎上做了進一步的研究，他們利用一組基于廣義諧和函數的變換首先將船舶橫搖方程降階為一組一階隨機微分方程，接著利用一個新的隨機平均程序獲得了幅值過程微分方程的平均漂移和擴散系數的閉合形表達式，接下來建立了控制橫搖幅值過程平均首次穿越時間的Pontryagin-Vitt方程。推導了Pontryagin-Vitt方程的兩個邊界條件，通過數值求解該邊界值問題獲得了平均首次穿越時間和首次穿越概率值。他們還首次研究了非線性阻尼系數對平均首次穿越時間的影響。

Cai等人[69-70]采用基于能量包線的隨機平均法研究了在隨機海浪中遭受外激和參激聯合作用的船舶的首次穿越問題。Yim[71]等人在2005年研究了一艘駁船的非線性耦合運動，建立了一個擬二自由度隨機模型，并進行了在隨機海浪中的穩性分析。由于非線性橫搖和升沉運動的耦合效應是明顯的，通過利用觀測到的升沉幅值試驗測量結果和波浪高程的強依賴性，他們將二自由度橫搖升沉模型中的升沉值表示為波高的函數，因而開發了一個精確和有效的擬二自由度模型。利用此擬二自由度模型基于首次穿越時間公式對此駁船進行了隨機穩性分析。根據美國海軍制定的運營和生存海況（1到9級），結果顯示在7級以上海況運營時，該駁船的可靠性顯著降低。

4.2 應用首次穿越理論時應注意的問題

建立在馬爾科夫擴散過程理論和隨機平均法之上的首次穿越理論是很嚴密和精深的，將其應用于船舶在隨機海浪上的穩性和傾覆預報可以說是一種非常積極和有意義的探索。但是對首次穿越理論本身的理解和將理論應用于具體問題都是有相當難度的，尤其是要達到使工業界的船舶工程師能理解這套理論并應用于日常的設計實踐中難度將更大，因而還需船舶教學和科研工作者們繼續為此做出不懈的努力。

5 研究展望

在新概念船型的初始開發過程中，特別是一些高性能特殊船型和一些軍用的高速艦船的初始開發設計中，穩性問題將是一個突出的問題，因為現行的穩性規范衡準僅在應用于普通常規船型時才是可靠的，在這方面，邁爾尼科夫分析可被用作為一個分析船舶動態穩性的高效的輔助工具。筆者認為諸如此類的針對邁爾尼科夫法的應用研究是很值得進行的。另外，在一些用邁爾尼科夫解析分析來處理有局限的問題上，例如船舶的隨浪穩性問題，是否可將邁爾尼科夫法和時域仿真配合起來使用？即先用邁爾尼科夫分析縮小應研究的船舶初始條件和控制參數的范圍，然后再有針對性地進行時域仿真，這將大大提高時域仿真的效率，作者認為在這方面也值得進行進一步的研究。

[1]王迎光,譚家華.對船舶完整穩性衡準的幾點思考[J].船舶標準化工程師,2007,40(238):11-14.

[2]Kobylinski L K,Kastner S.Stability and safety of ships.Vol.I,Regulation and operation[M].Elsevier ocean engineering book series;v.9,Amsterdam;Boston:Elsevier,2003:168-169.

[3]Alberto Francescutto.Intact ship stability:The way ahead[J].Marine Technology,2004,41(1):31-37.

[4]Rojas L P,Belenky V L.A review of the stability of ship and ocean vehicles conference(STAB’2003)[J].Marine Technology,2005,42(1):21-30.

[5]Froude W.On the rolling of ships[J].Transactions of Institute of Naval Architects,1861,2:180-229.

[6]Krylov A N.A general theory of the oscillation of a ship in waves[J].Transactions of Institute of Naval Architects,1898,40:135.

[7]Korvin-Kroukovsky B V.Investigation of ship motions in regular waves[J].SNAME Trans,1955,63:386-435.

[8]Lewis E V.Principles of naval architecture,Volume 3,Motions in waves and controllability[M].Society of Naval Architects and Marine Engineers,1988.

[9]Salvesen N,Tuck E O,Faltinsen O M.Ship motions and sea loads[J].Transactions of the Society of Naval Architects and Marine Engineers,1970,78:250-287.

[10]De Kat Jan O,Paulling J R.The simulation of ship motions and capsizing in severe seas[J].SNAME Transactions,1989,97:139-168.

[11]McTaggart,Kevin A.Ship capsize risk in a seaway using fitted distributions to roll maxima[J].Journal of Offshore Mechanics and Arctic Engineering,Transactions of the ASME,2000,122(2):141-146.

[12]De Kat Jan O,Randolph P J.Prediction of extreme motions and capsizing of ships and offshore marine vehicles[C]//Proceedings of the International Conference on Offshore Mechanics and Arctic Engineering-OMAE.2001,1:817-828.

[13]De Kat Jan O,Pinkster,Dirk-Jan,McTaggart,Kevin A.Random waves and capsize probability based on large amplitude motion analysis[C]//Proceedings of the International Conference on Offshore Mechanics and Arctic Engineering-OMAE.2002,4:685-694.

[14]王迎光,譚家華.隨機激勵下非線性海洋結構物響應分析方法研究進展[J].海洋工程,2007,25(4):112-119.

[15]王迎光,劉小軍,譚家華.用時域仿真求解一隨機振蕩系統的水準跨越率[J].振動與沖擊,2007,26(2):37-38;55.

[16]Shinozuka M,Deodatis G.Simulation of stochastic processes by spectral representation[J].Applied Mechanics Reviews,ASME,1991:191-204.

[17]Shinozuka M,Wai P.Digital simulation of short-crested sea surface elevations[J].Journal of Ship Research,1979,23(1):855-874.

[18]Naess A.Extreme value estimates based on the envelop concept[J].Applied Ocean Research,1982,4(3):181-187.

[19]Naess A.Technical note:On a rational approach to extreme value analysis[J].Applied Ocean Research,1984,6(3):173-174.

[20]Naess A.Technical note:On the long term statistics of extremes[J].Applied Ocean Research,1984,6(4):227-228.

[21]Wang Y G（王迎光）,Xue L P（薛雷平）,Tan J H（譚家華）.Surge response of a compliant offshore structure by time domain simulation[J].Journal of Shanghai Jiao Tong University,2007,E-12(6):838-844.

[22]王迎光.隨機海況下海洋結構物慢漂極端響應和穩性研究[D].上海:上海交通大學船舶與海洋工程系,2008.

[23]Guckenheimer John,Holmes Philip.Nonlinear oscillations,dynamical systems,and bifurcations of vector fields[M].Applied Mathematical Sciences(Springer-Verlag New York Inc.),1983,42.

[24]Wiggins S.Global Bifurcation and Chaos[M].New York:Springer,1988.

[25]Moon F C.Chaotic and Fractal Dynamics[M].New York:Wiley,1992.

[26]Lin Huan,Yim C S.Chaotic roll motion and capsize of ships under periodic excitation with random noise[J].Applied O-cean Research,1995,17:185-204.

[27]Thompson J M T.Designing against capsize in beam seas:Recent advances and new insights[J].Applied Mechanics Reviews,1997,50:307-325.

[28]Wang Yingguang（王迎光）,Tan Jiahua（譚家華）.Global geometric analysis of ship rolling and capsizing in random waves[J].China Ocean Engineering,2007,21(4):577-586.

[29]Makoto Kan,Harukuni Taguchi,Toshihiko Saruta,Mikio Yasuno.Capsizing of a ship in quartering seas,Part 1,Model experiments on mechanism of capsizing[J].日本造船學會論文集,1990(167):81-90.

[30]Makoto Kan,Harukuni Taguchi.Capsizing of a ship in quartering seas,Part 2,Chaos and fractal in capsizing phenomenon[J].日本造船學會論文集,1990(168):211-220.

[31]Makoto Kan,Harukuni Taguchi.Capsizing of a ship in quartering seas,Part 3,Chaos and fractal in asymmetric capsize equation[J].日本造船學會論文集,1991(169):1-13.

[32]Makoto Kan,Harukuni Taguchi.Ship capsizing and chaos,in nonlinearity and chaos in engineering dynamics(Thompson J M T and Bishop S R eds)[M].Wiley,Chichester,1994:418-420.

[33]Falzarano J M,Shaw S W,Troesch A W.Application of global methods for analyzing dynamical systems to ship rolling motion and capsizing[J].International Journal of Bifurcation and Chaos[in Applied Sciences and Engineering],1992,2(1):101-115.

[34]Falzarano J M.Predicting complicated dynamics leading to vessel capsizing[D].Michigan:Department of Naval Architecture and Marine Engineering,the University of Michigan.1990.

[35]Hsieh Shang-Rou,Troesch A W,Shaw S W.Nonlinear probabilistic method for predicting vessel capsizing in random beam seas[C]//Proceedings of The Royal Society of London,Series A:Mathematical and Physical Sciences,1994,446:195-211.

[36]Bikdash M,Balachandran B,Nayfeh A.Melnikov analysis for a ship with a general roll-damping model[J].Nonlinear Dynamics,1994,6:101-124.

[37]Jiang Changben.Highly nonlinear rolling motion leading to capsize[D].Michigan:Department of Naval Architecture and Marine Engineering,the University of Michigan,1995.

[38]Jiang Changben,Troesch A W,Shaw S W.Highly nonlinear rolling motion of biased ships in random beam seas[J].Journal of Ship Research,1996,40(2):125-135.

[39]Chen S L,Shaw S W.A fast manifold approach to Melnikov functions for slowly varying oscillators[J].International Journal of Bifurcation and Chaos,1996,6:1575-1578.

[40]Chen S L.Modeling,dynamics and control of large amplitude motions of vessels in beam seas[D].Michigan:Department of Mechanical Engineering,Michigan State University,1996.

[41]Chen S L,Shaw S W.Phase space transport in a class of multi-degree-of-freedom systems[C]//Propceedings of the 1997 ASME Design Engineering Technical Conferences.Sacramento,Calif,1997.

[42]Chen S L,Shaw S W,Troesch A W.A systematic approach to modeling nonlinear multi-DOF ship motions in regular seas[J].Journal of Ship Research,1999,43(1):25-37.

[43]Scolan Y M.Technical note on ship rolling associated to high degree polynomial restoring moment using the Melnikov method[J].Applied Ocean Research,1997,19:225-234.

[44]Jiang C,Troesch A W,Shaw S W.Capsize criteria for ship models with memory-dependent hydrodynamics and random excitation[J].Phil.Trans.R.Soc.Lond.A,2000,358(1771):1761-1791.

[45]Spyron K J,Thompson J M T.The nonlinear dynamics of ship motions:A field overview and some recent developments[J].Phil.Trans.R.Soc.Lond.A,2000,358(1771):1735-1760.

[46]Spyrou K J,Cotton B,Gurd B.Analytical expressions of capsize boundary for a ship with roll bias in beam waves[J].Journal of Ship Research,2002,46(3):167-174.

[47]McCue L S.Chaotic vessel motions and capsize in beam seas[D].Michigan:Department of Naval Architecture and Marine Engineering,University of Michigan,2004.

[48]Spyrou K J.Asymmetric surging of ships in following seas and its repercussions for safety[J].Nonlinear Dynamics,2006,43:149-172.

[49]沈 棟.隨機橫浪作用下船舶傾覆概率的研究[D].上海:上海交通大學,1999.

[50]沈 棟,黃祥鹿.隨機波浪作用下的船舶傾覆[J].船舶力學,1999,3(5):7-14.

[51]紀 剛,張緯康.船舶橫搖的安全池研究[J].中國造船，2002,43(4):25-31.

[52]袁 遠,余 音,金咸定.船舶在規則波中的奇異傾覆[J].上海交通大學學報,2003,37(7):995-998.

[53]袁 遠,余 音,金咸定.船舶在隨機橫浪中的奇異傾覆機理[J].船舶力學,2004,8(1):44-50.

[54]金咸定,余 音,袁遠.船舶在規則橫浪中的全局穩定性[J].振動與沖擊,2003,22(1):85-87.

[55]唐友剛,谷家揚,鄭宏宇,李紅霞.用Melnikov方法研究船舶在隨機海浪中的傾覆[J].船舶力學,2004,8(5):27-34.

[56]劉利琴,唐友剛,李紅霞.船舶運動的復雜動力特性在我國的研究進展[J].武漢理工大學學報（交通科學與工程版）,2006(1):183-186.

[57]浦金云,張緯康,陳曉洪,何其偉,紀 剛.具有淹水艙的艦船橫搖運動建模探討[J].船舶力學,2007,11(1):47-54.

[58]Lee Young-Woo.Nonlinear ship motion models to predict capsize in regular beam waves[D].Michigan:Department of Naval Architecture and Marine Engineering,the University of Michigan,2001.

[59]Zhu W Q,Wu Y J.First-passage time of Duffing oscillator under combined harmonic and white-noise excitations[J].Nonlinear Dynamics,2003,32(3):291-305.

[60]Roberts J B.First-passage probabilities for non-linear oscillators[J].Journal of Engineering Mechanics,1976,102:851-866.

[61]Roberts J B.First-passage time for oscillators with non-linear restoring force[J].Journal of Sound and Vibration,1978,56:71-86.

[62]Roberts J B.First-passage time for oscillators with non-linear damping[J].Journal of Applied Mechanics,1978,45:175-180.

[63]Roberts J B.First-passage probabilities for randomly excited systems:Diffusion methods[J].Probabilistic Engineering Mechanics,1986,1(2):66-81.

[64]Roberts J B,Spanos P D.Stochastic averaging:An approximate method of solving random vibration problems[J].Int.J Non-linear Mech,1986,21:111-134.

[65]Roberts J B.A stochastic theory for nonlinear ship rolling in irregular seas[J].Journal of Ship Research,1982,26(4):229-245.

[66]Roberts J B.Response of an oscillator with non-linear damping and a softening spring to non-white random excitation[J].Probabilistic Engineering Mechanics,1986,1(1):40-48.

[67]Roberts J B,Vasta M.Markov modelling and stochastic identification for nonlinear ship rolling in random waves[J].Philosophical Transactions of the Royal Society A:Mathematical,Physical and Engineering Sciences 15,2000,358(1771):1917-1941.

[68]Wang Yingguang（王迎光）,Huang Zhilong（黃志龍）,Tan Jiahua（譚家華）.First passage probability of nonlinear ship rolling in random seas[J].Journal of Ship Mechanics,2008,12(6):870-879.(En English)

[69]Cai G Q,Yu S J,Lin Y K.Ship rolling in random sea,stochastic dynamics and reliability of nonlinear ocean systems[J].ASME DE,1994,77:81-88.

[70]Shlesinger M F,Swean T(Thomas).Stochastically excited nonlinear ocean structures[M].Singapore,New Jersey:World Scientific,1998:129-155.

[71]Yim S C S,Tongchate Nakhata,Huang E T.Coupled nonlinear barge motions,Part two:Stochastic models and stability analysis[J].Journal of Offshore Mechanics and Arctic Engineering,2005,127:83-95.