艦船用兩級行星傳動系統的固有頻率嚙合剛度敏感度分析
趙永強,李瑰賢 ,常 山,張 祥
(1哈爾濱工業大學機電工程學院,哈爾濱 150001;2中船重工集團第703研究所,哈爾濱 150036)
1 引 言
行星齒輪傳動系統應用非常廣泛,它的動力學分析對減振降噪具有重要的指導意義。固有頻率對系統參數的敏感度能夠為系統響應的降低、結構設計的優化提供重要的依據。選擇調節好系統參數可以平衡各設計目標。
有些文獻已經對單級行星齒輪傳動系統的固有頻率參數敏感度進行了研究,Botman[1]和Cunliffe[2]研究了行星輪支撐剛度變化對系統固有頻率的影響,Kahraman[3]使用純扭轉模型研究了嚙合與支撐剛度對系統固有頻率的影響,Saada和Velex[4]研究了自由振動齒圈支撐剛度對系統固有頻率的影響,Lin和Parker[5]系統地研究了嚙合與支撐剛度、齒輪質量與轉動慣量、行星架轉速等參數對系統固有頻率的影響。
本文對大型艦船機械裝置中常用的兩級人字齒行星齒輪系統進行了固有頻率敏感度的分析,文中主要對嚙合剛度的敏感度進行了系統的研究,得出了各振動模態中固有頻率隨參數變化的情況。
2 系統動力學模型
本文使用自己建立的模型,建模時采用集中參數法。齒輪均為人字齒輪,中心輪浮動,不考慮齒間側隙的影響。整個系統由行星輪系和行星架固定的星形輪系相互聯接而成。
由于采用人字齒的結構型式,所以只需考慮三個方向的自由度。系統共有3×(M+2+N+3)個自由度(M、N分別為星輪和行星輪個數),系統的自由振動的動力學方程為

式中,M、G、C、kb、km、kω分別為系統的質量矩陣、陀螺矩陣、阻尼矩陣、支撐剛度矩陣、嚙合剛度矩陣和向心剛度矩陣。
3 特征值敏感度的計算方法
特征值敏感度分析主要是計算固有頻率和振動模態對系統參數的導數,這里只研究對動態特性影響較大的系統參數,如嚙合剛度。考察下式的特征值問題

本文使用模態法來計算系統的特征值的導數,再根據固有頻率與特征值導數之間的關系,就可以計算出各系統參數對固有頻率的敏感度。
特征值為單根時的敏感度為
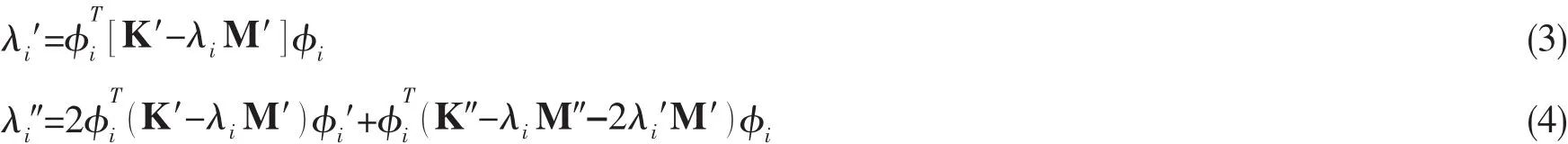
特征值為重根時的敏感度為
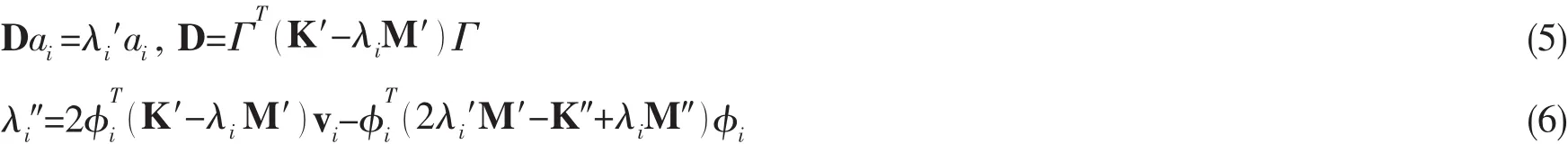
上述公式中各量的具體描述詳見文獻[5]。
4 嚙合剛度敏感度
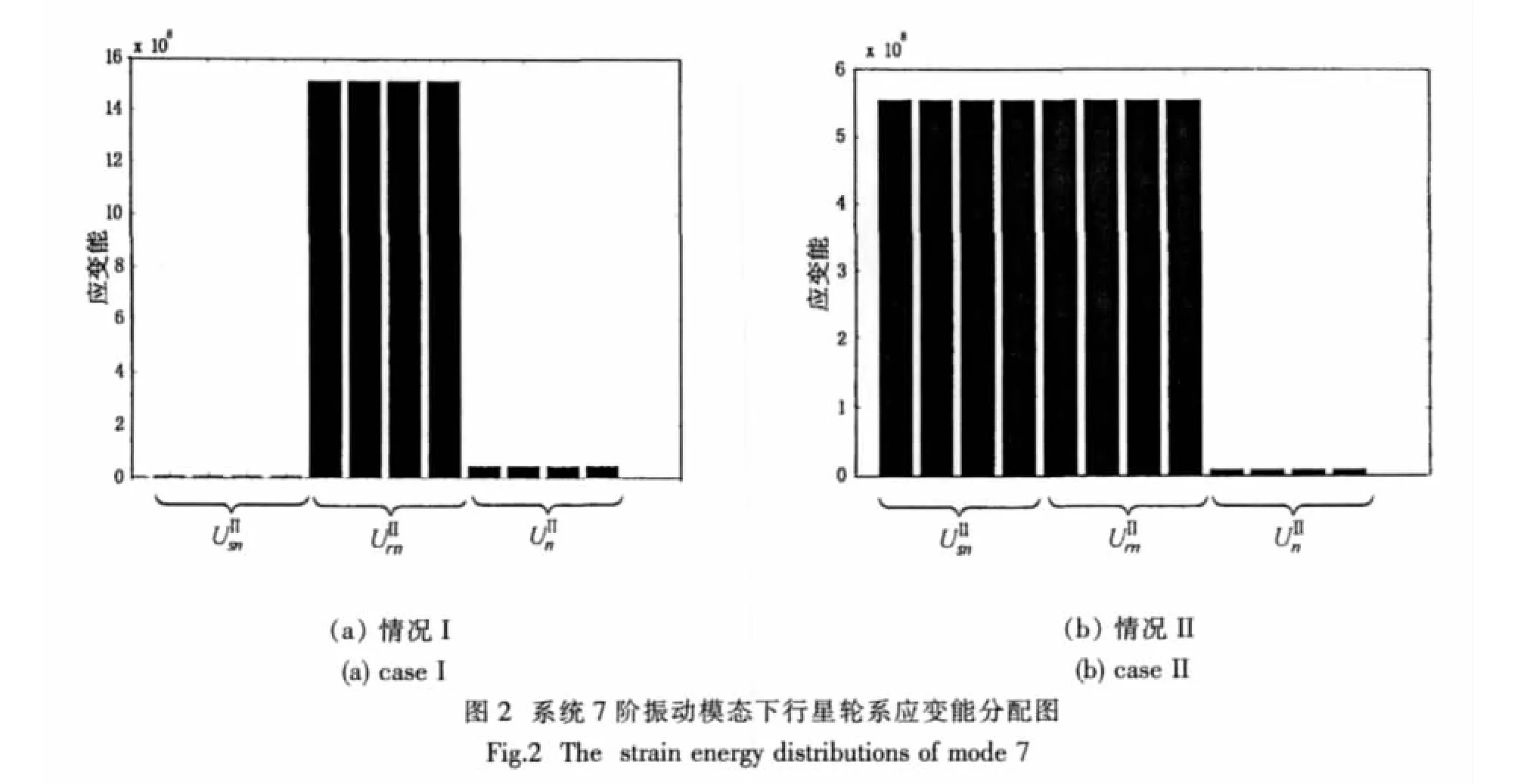
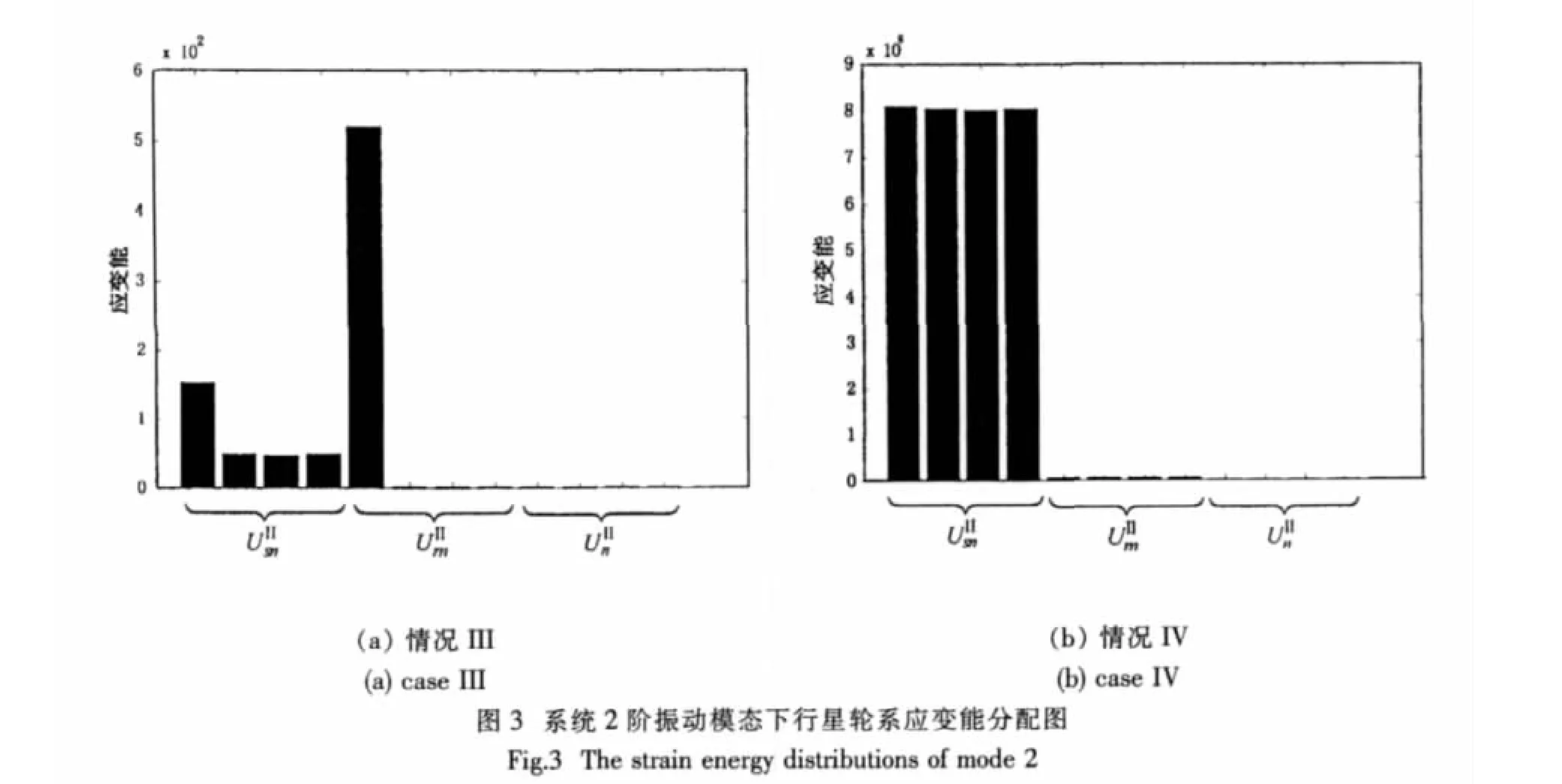
所研究的嚙合剛度包括行星輪系與星形輪系中各對互相嚙合的齒輪,其中某些剛度的敏感度與其相應的模態應變能對應,接下來的分析可以驗證這一現象。
4.1 行星輪系太陽輪與行星輪嚙合剛度敏感度
4.1.1 可調諧系統

對于耦合輪系振動模態,系統的固有頻率均為單根,將公式(7)代入(3)、(4)式,并利用下式

可以得到單根情況下特征值敏感度的計算公式:

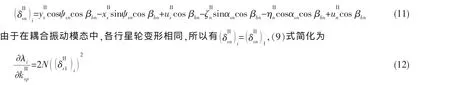
行星輪系統振動模態中,特征值為重根,只考慮 λ1=λ2的情況,λ1′、λ2′為(5)式中矩陣 D 的特征值,將(7)式代入(5)式,得

在單級行星齒輪傳動系統的平移(直齒)或徑向平移—扭擺(斜齒)振動模態中但在本文研究的兩級人字齒行星傳動系統中,此種情況不成立。而在N>3時才出現的、重數為N-3的固有頻率振動模態下,有λ1,2′在 N=4 和 N=5 的情況下才可以寫成(9)式的形式;N>5 時矩陣D的特征值很難求得封閉解,需采用數值方法。
對于星形輪系振動模態,當星輪個數M≤3時,特征值為單根,M>3時出現重數為M-3的特征值,但無論對于單根特征值還是重根特征值,均有(行星輪系不振動),所以,固有頻率對的敏感度均為零。
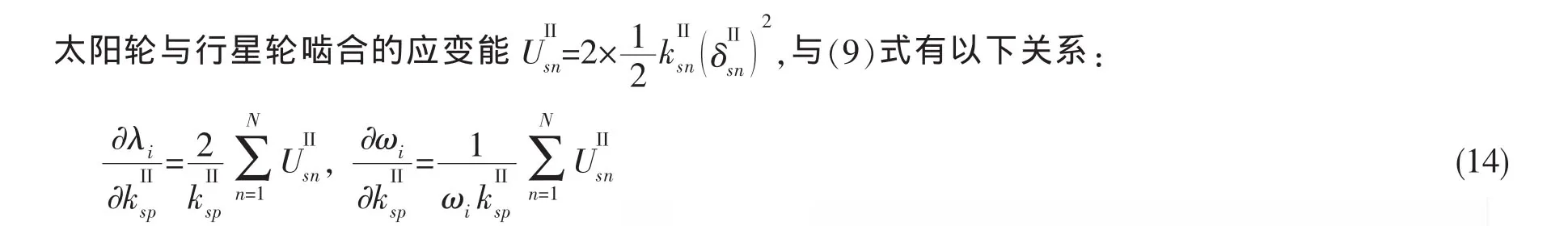
本文以大功率艦船用兩級人字齒行星齒輪傳動系統為例(見表1),研究其固有頻率對的敏感度。
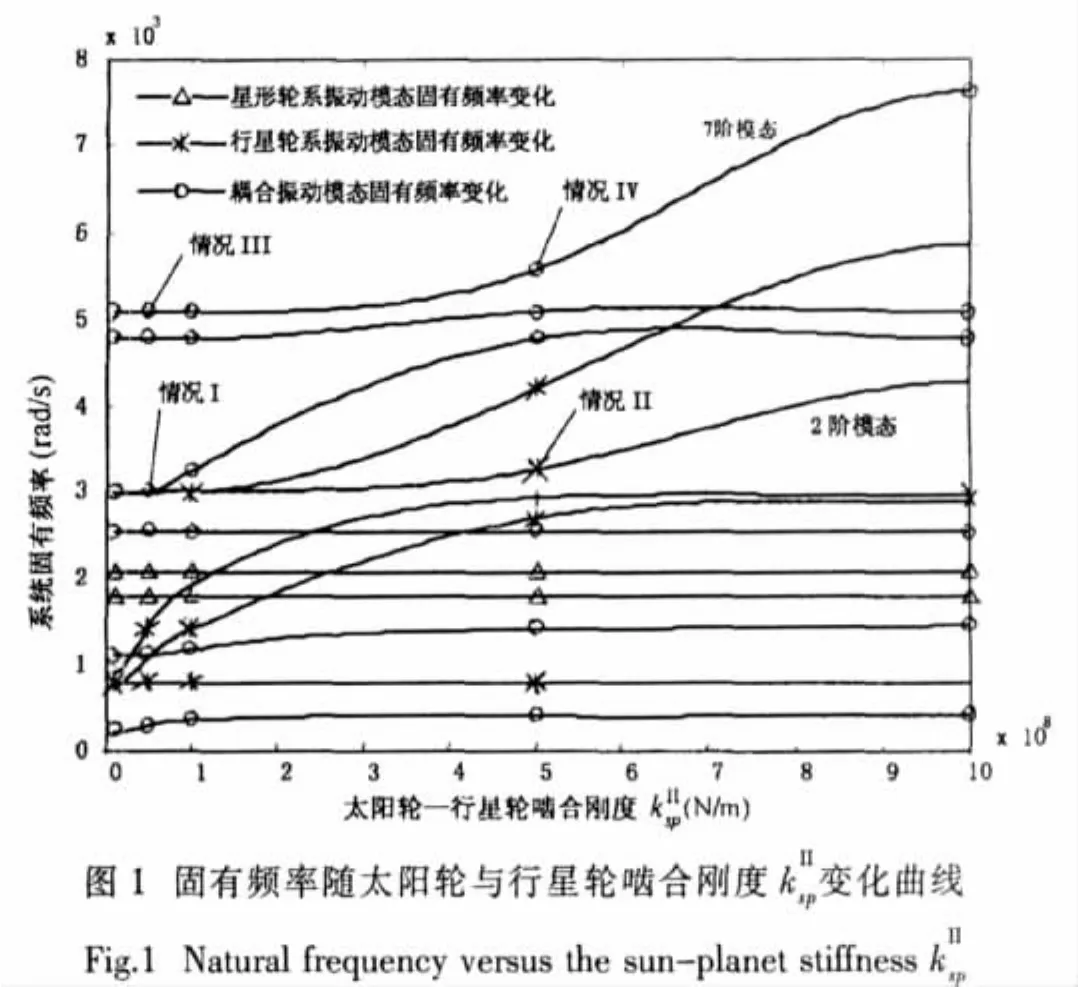
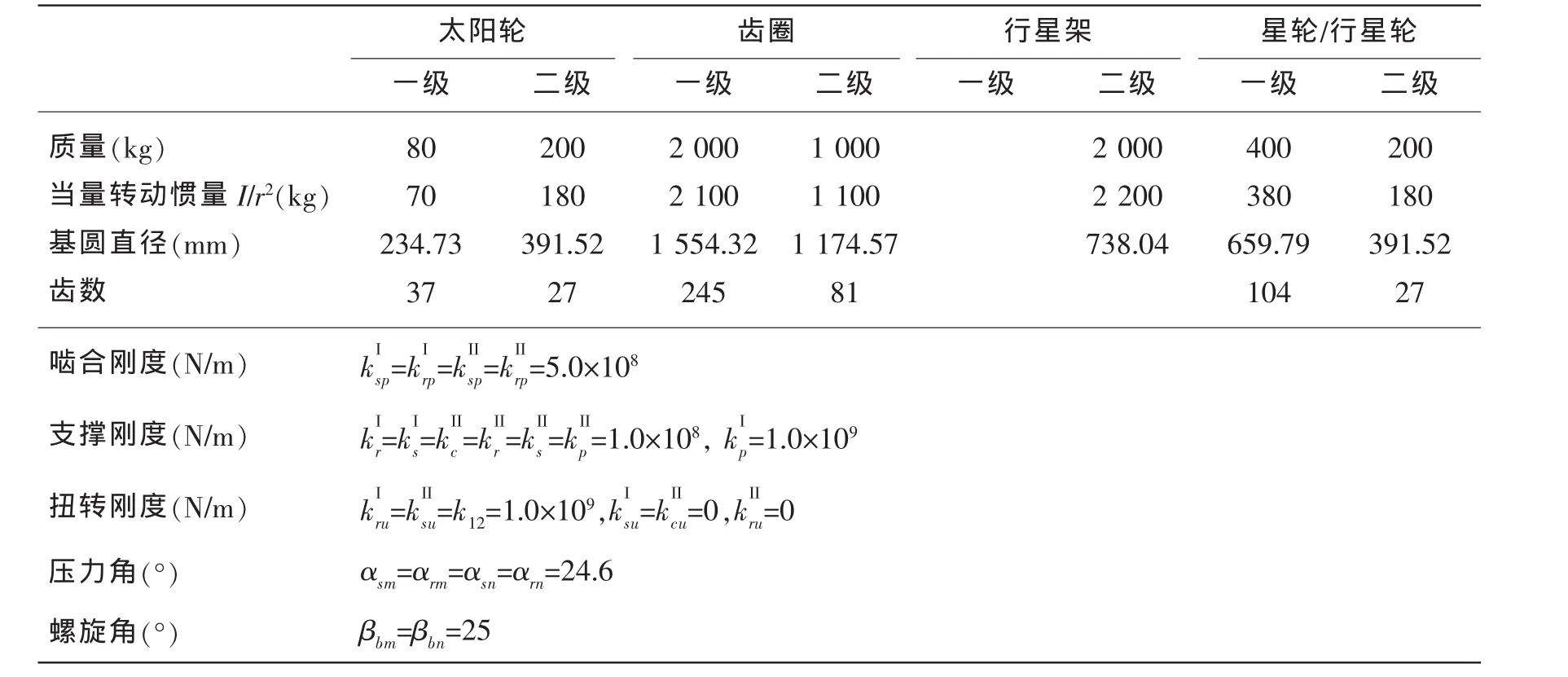
表1 系統參數表Tab.1 Model parameters of two stage double tooth planetary gear trains
4.1.2 不可調諧系統
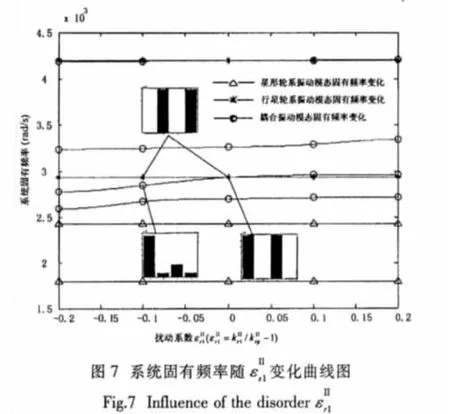
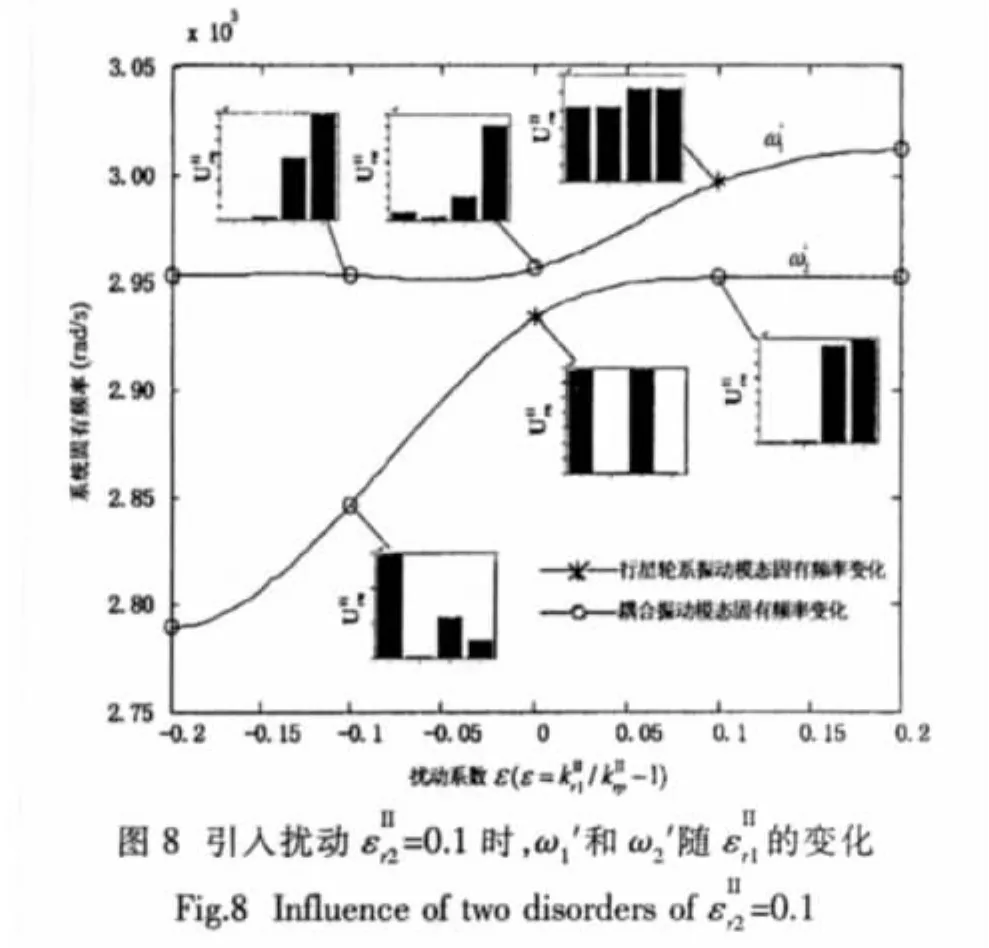
在實際的行星齒輪傳動中,由于行星輪的加工裝配誤差、與太陽輪接觸齒數的變化等因素的影響,使得各行星輪與太陽輪間的嚙合剛度產生差異,從而使整個系統變得不可調諧。所以,有必要研究非調諧情況下,行星輪與太陽輪嚙合剛度變化對系統模態特性的影響。假定只有第一個行星輪與太陽輪嚙合剛度發生變化,系統質量矩陣和剛度矩陣對的導數為:
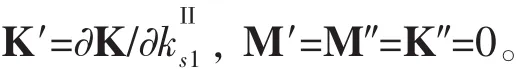
對于耦合輪系振動模態,固有頻率均為單根,利用(3)、(4)式得特征值敏感度計算公式如下:


對于行星輪系振動模態,系統固有頻率為重根,先考慮λ1=λ2的情況,選取任意的正交模態振型為Γ=[γ1,γ2],符號表示在模態γi下太陽輪與第一個行星輪嚙合的彈簧變形量,這一定義類似于在模態φi下的太陽輪與行星輪嚙合的彈簧變形量(5)式中矩陣 D 及其特征值 (λ1′、λ2′)為

對于星形輪系振動模態,第二級行星輪系無振動,所以系統固有頻率對的敏感度均為零。
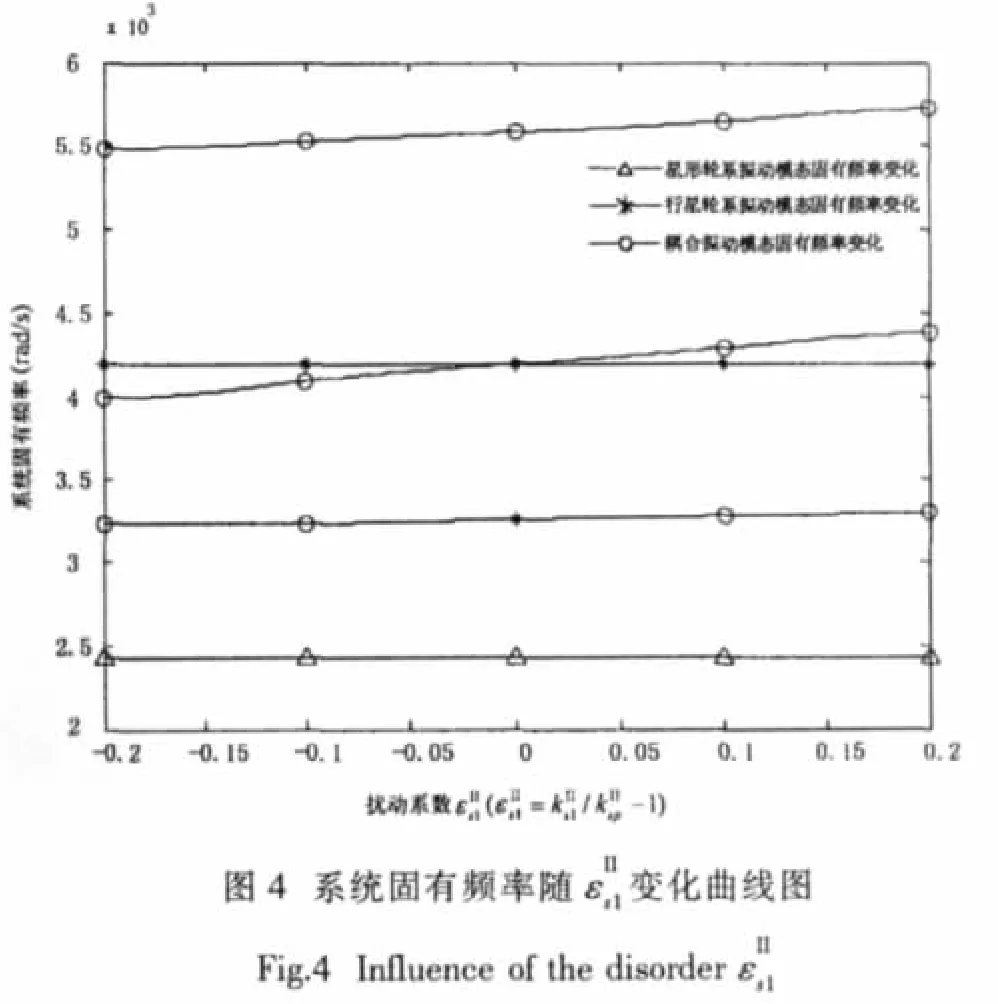
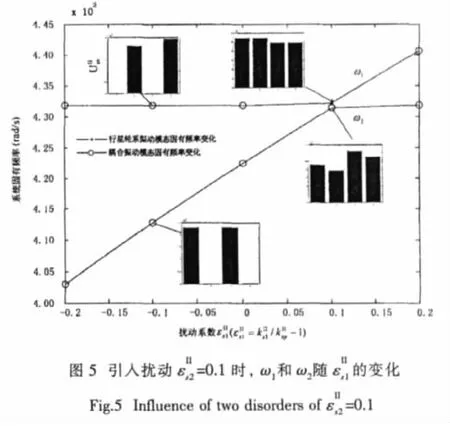
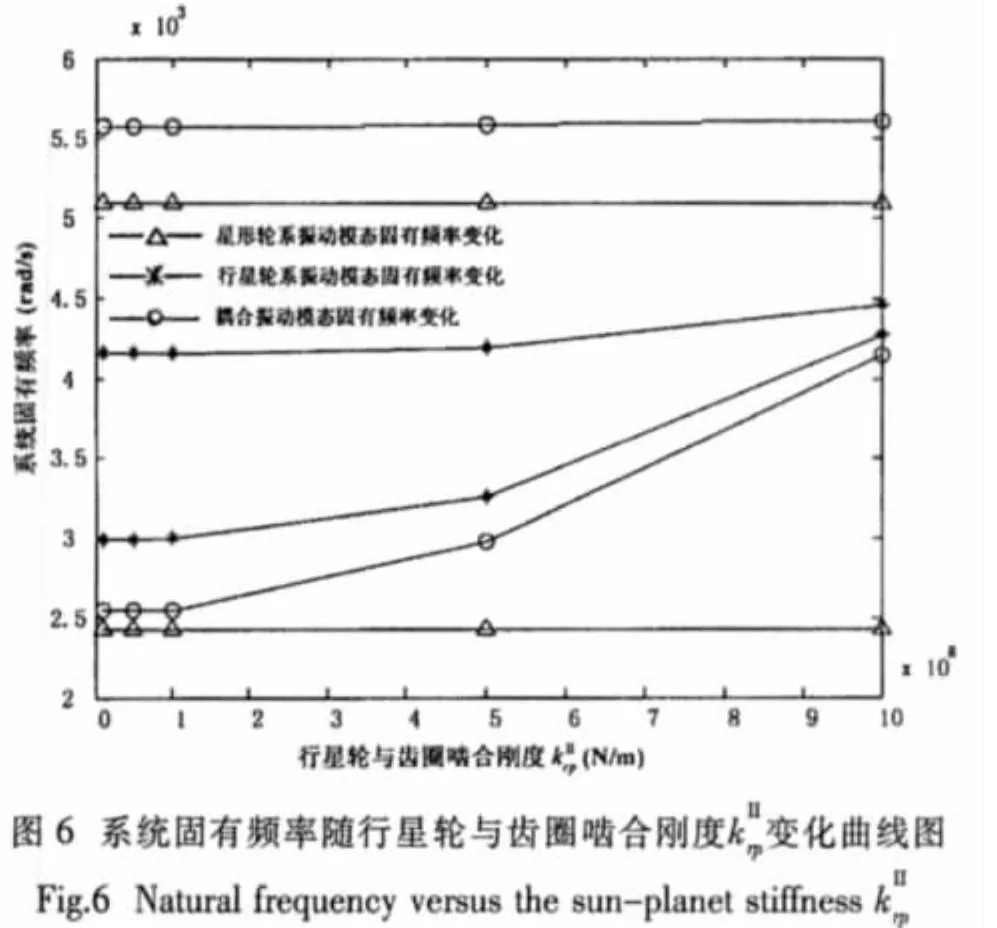
4.2 行星輪系行星輪與齒圈嚙合剛度敏感度
4.2.1 可調諧系統
使用4.1.1節中類似的方法,可以得到各振動模態下固有頻率敏感度的計算公式,這里只給出耦合振動模態下的計算公式:

4.2.2 不可調諧系統
特征值敏感度的計算分析方法與4.1.2節類似,這里不再給出具體的計算公式。
4.3 星形輪系嚙合剛度敏感度
星形輪系固有頻率對嚙合剛度的敏感度計算,類似于行星輪系,這里不再詳述。
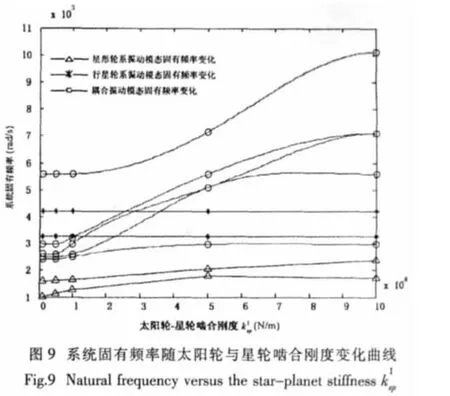
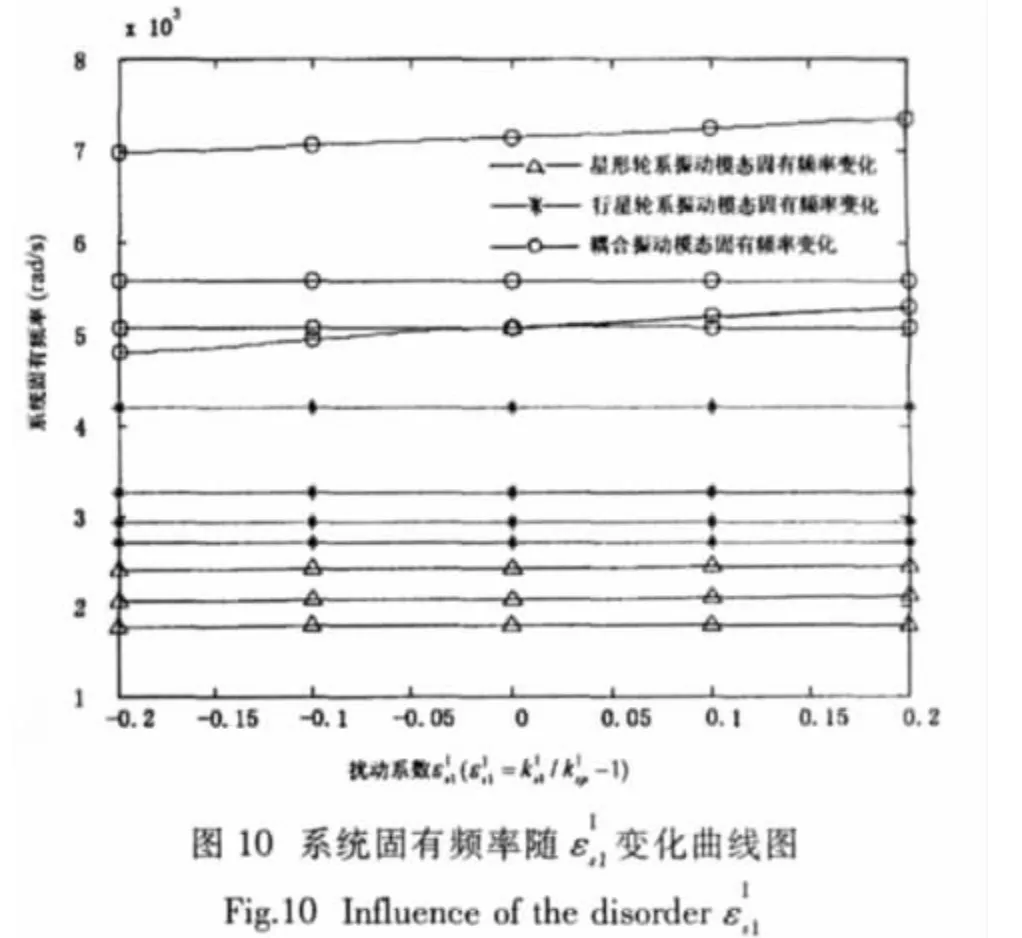
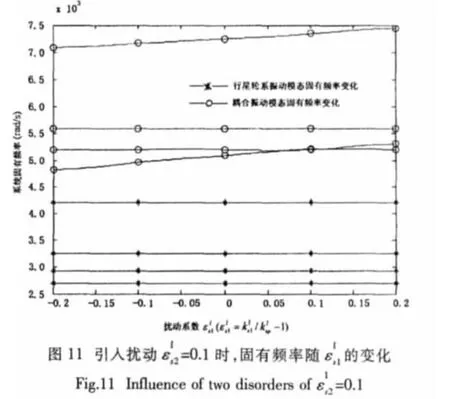
系統固有頻率隨星形輪系太陽輪與星輪嚙合剛度的變化如圖9所示,從圖中可以看出的變化對耦合振動模態固有頻率的影響最大,對行星輪系沒有影響。引入擾動后的變化只對耦合振動模態的固有頻率有影響,但影響明顯變小(圖10)。引入參數后,系統無星形輪系振動模態的變化只對耦合振動模態的固有頻率有影響,但影響很小(圖11)。
5 結 論
(1)利用兩級人字齒行星傳動的振動模態特性,對敏感度的計算公式進行了簡化,并建立了敏感度與模態應變能的關系;
(2)通過應變能的變化反映出了固有頻率的變化趨勢,得到了各振動模態中固有頻率隨系統各嚙合剛度的變化規律,從而為系統振動的減小和結構的優化提供了重要的參考數據。
[1]Botman M.Epicyclic gear vibrations[J].ASME Journal of Engineering for Industry,1976,96:811-815.
[2]Cunliffe F,Smith J D,Welbourn D B.Dynamic tooth loads in epicyclic gears[J].ASME Journal of Engineering for Industry,1974,94:578-584.
[3]Kahraman A.Natural modes of planetary gear trains[J].Journal of Sound and Vibration,1994,173:125-130.
[4]Saada A,Velex P.An extended model for the analysis of the dynamic behavior of planetary trains[J].ASME Journal of Mechanical Design,1995,117:241-247.
[5]Lin J,Parker R G.Sensitivity of planetary gear natural frequencies and vibration modes to model parameters[J].Journal of Sound and Vibration,1999,228:109-128.

