應用于變頻空調系統的無速度傳感器矢量控制研究＊

蘭州理工大學 電信學院（甘肅蘭州730050） 李曉英 王言徐

1 引言

變頻空調通過調節壓縮機電機轉速來改變壓縮機單位時間的排氣量，從而改變制冷系統中循環的制冷劑流量，達到調節環境溫度的目的。能效比是衡量變頻空調性能的重要指標。通常壓縮機電機低速運行時能效比高，而高速運行時能效比低[1]。然而，當電機低速運行時，由于壓縮機吸氣、壓縮、排氣的物理過程會引起較大的轉矩脈動，從而導致壓縮機電機的轉速波動。可見，需提高能效比和降低轉速波動之間存在矛盾。變頻壓縮機普遍采用V/f恒定的開環控制方法，由于沒有速度閉環，低速范圍轉速波動以及由此帶來的壓縮機震動和噪聲問題更為突出。要減小壓縮機轉速波動，需引入速度反饋，然而壓縮機的機械結構決定了很難在其內部安裝速度傳感器。

為解決這一問題，本文采用無速度傳感器矢量控制方案，不引入速度傳感器，用轉速估計算法獲得速度信號進行閉環控制，以改善變頻空調控制系統的動態響應，減小由于轉速波動帶來的壓縮機震動和噪聲。無速度傳感器矢量控制的關鍵在于轉子磁鏈的觀測和轉速估計，針對這兩個核心問題，本文構造了改進電壓型磁鏈觀測模型，并基于PI自適應控制方法實現轉速估算。

2 轉子磁鏈觀測

由于按轉子磁場定向時，定子電流的勵磁分量和轉矩分量之間可實現完全解耦，且轉子磁鏈的表達形式最為簡單（僅與定子電流的勵磁分量有關），故本文采用按轉子磁場定向的矢量控制策略。要實現按轉子磁場定向的矢量控制，必須獲得轉子磁鏈信號，即必須對轉子磁鏈進行觀測。轉子磁鏈觀測的準確與否，直接影響到電機定子電流中的勵磁分量和轉矩分量能否實現真正解耦[2，3]。因此轉子磁鏈的準確定向及觀測至關重要。在實際系統中，通常借助于容易測量的電壓、電流等信號構造轉子磁鏈模型來間接計算磁鏈的大小與相位。

異步電動機在靜止兩相坐標系下的電壓方程為：

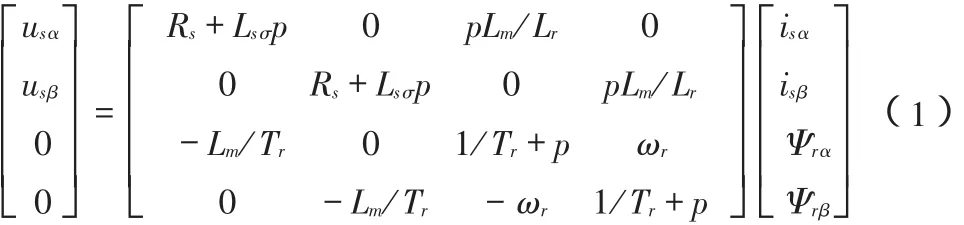
式中，usα、usβ分別為 α 軸和 β 軸的定子電壓；isα、isβ分別為 α 軸和β 軸的定子電流；Ψrα、Ψrβ分別為 α 軸和 β 軸的轉子磁鏈；Rs、Rr分別為定子電阻和轉子電阻；Ls、Lr、Lm分別為定子電感、轉子電感和互感；Lsσ=σLs為考慮漏感時定子的等效電感，σ為漏感系數；Tr=Lr/Rr為轉子時間常數；ωr為轉子角速度；p為微分算子。由式（1）可得常用的兩種轉子磁鏈觀測模型[1]：

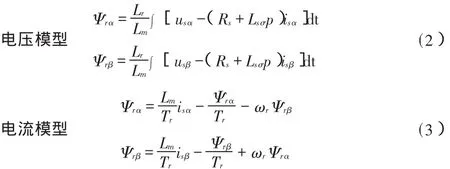
比較式（2）、式（3）不難發現，相對于電流模型，電壓模型具有算法簡單、不含轉子電阻等優點；并且電壓模型僅通過測量定子電壓、電流即可估計轉子磁鏈，不需要轉速信息。因此，電壓型轉子磁鏈觀測模型比較適用于無速度傳感器變頻調速系統。

雖然電壓模型在高速時性能較好，然而電壓模型中磁鏈是由反電動勢積分得到的，在電機低速運行時產生的反電動勢較小，影響磁鏈觀測的準確性；此外，模型中的純積分環節在實際應用時會帶來直流漂移和誤差累積等問題，低速時會降低磁鏈觀測的精度，進而會使得整個控制系統性能下降。當電壓模型應用于變頻空調控制系統時，解決純積分環節帶來的直流漂移和誤差累積等問題、提高低速時磁鏈觀測的精度顯得尤為重要。

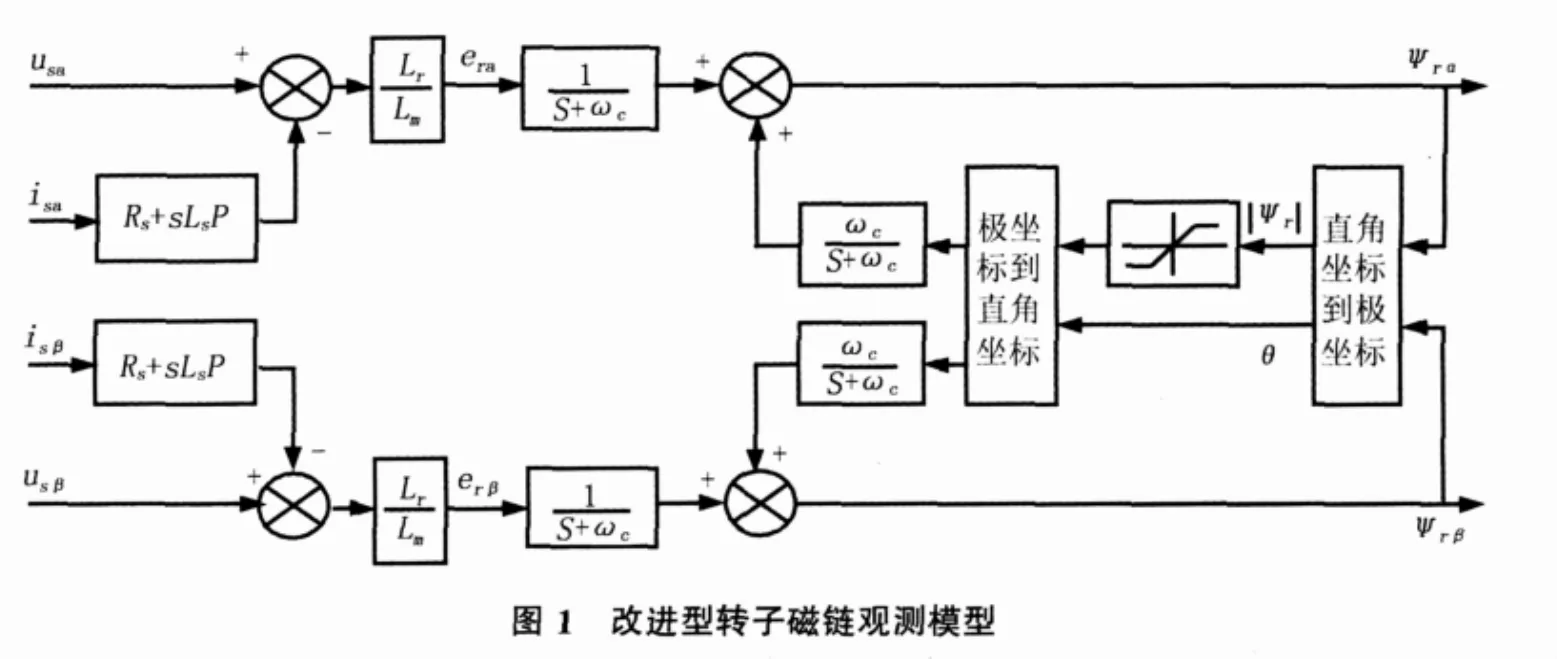
在保持電壓模型中、高速的良好性能基礎上，本文對純積分環節加以改進，引入一種帶限幅反饋環節的積分器代替純積分器。改進型轉子磁鏈觀測模型如圖1示。

圖中 erα、erβ分別為α軸和β軸的轉子反電動勢，表達式如下：

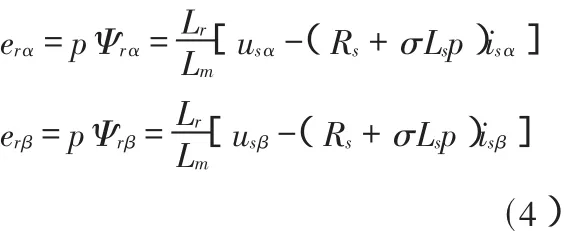
｜Ψr｜、θ分別為轉子磁鏈的幅值與位置角：

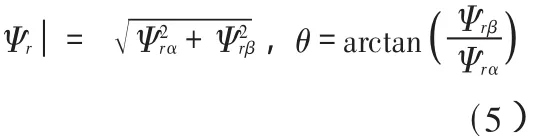
改進型磁鏈觀測模型中，帶限幅反饋環節的積分器在消除純積分器直流漂移的同時不會引入轉子磁鏈的幅值與相位誤差。

3 轉速估算

轉速估計是無速度傳感器矢量控制系統的又一核心問題。國內外已有多種估算轉速的方法，如PI自適應法、直接計算法、模型參考自適應法（MRAS）、高頻注入法及擴展卡爾曼濾波法等[1,3]。在變頻調速控制系統中，宜采用速度估計的穩態特性和動態特性綜合指標較高的估算方法，還應考慮到實現起來簡單。高頻注入法及擴展卡爾曼濾波法由于計算量龐大，在實際系統中一般不采用。本文采用基于PI調節器的自適應法估計轉子轉速。

根據電機的機電運動方程式：

考慮控制過程中 Ψrd保持恒定，則 Te由 isq決定，轉矩的誤差信號可以由給定轉矩電流分量與實際響應 isq的差值反映出來，將（－ isq）送入 PI調節器，輸出即為轉速的估算值 ωr，即

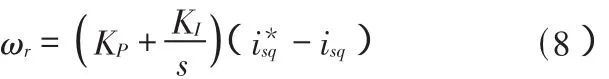
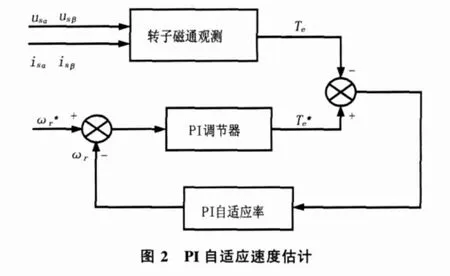
這種基于PI調節器的自適應速度估計法可以認為是模型參考自適應（MRAS）法的變形，在模型參考自適應法的基礎上采用PI自適應機制，從電流轉矩分量的誤差信號得到轉子速度的估計，其結構較模型參考自適應法簡單[4]，如圖2所示。

圖中，可將轉子磁通觀測得到的 Te看作參考模型，而看作可調模型，利用兩模型輸出值的誤差來調整中的 ωr，直到兩模型的輸出值相等，即－Te=0時，認為 ωr為實際轉速。PI調節自適應法轉速估算關系式：

式中，KP、KI為PI調節器參數。

4 無速度傳感器矢量控制系統仿真

4.1 系統結構

基于上述轉子磁鏈觀測以及轉速估計原理的變頻空調矢量控制系統結構如圖3示。

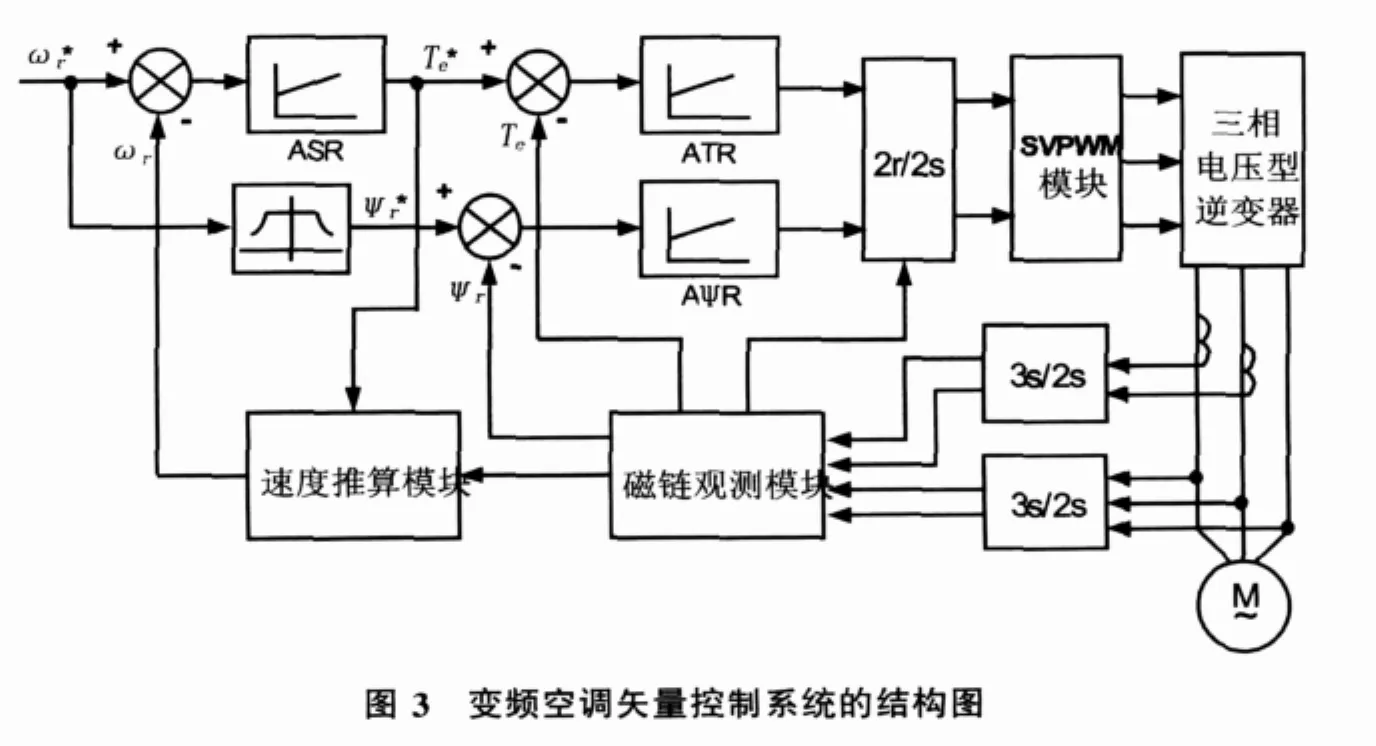
圖中，速度調節器ASR、轉矩調節器ATR以及磁通調節器AΨR均采用PI控制。磁鏈觀測模塊采用帶限幅反饋的改進電壓型磁鏈觀測模型，速度推算模塊采用PI自適應法進行轉速估算。變頻空調壓縮電機由三相SVPWM電壓型逆變器供電。

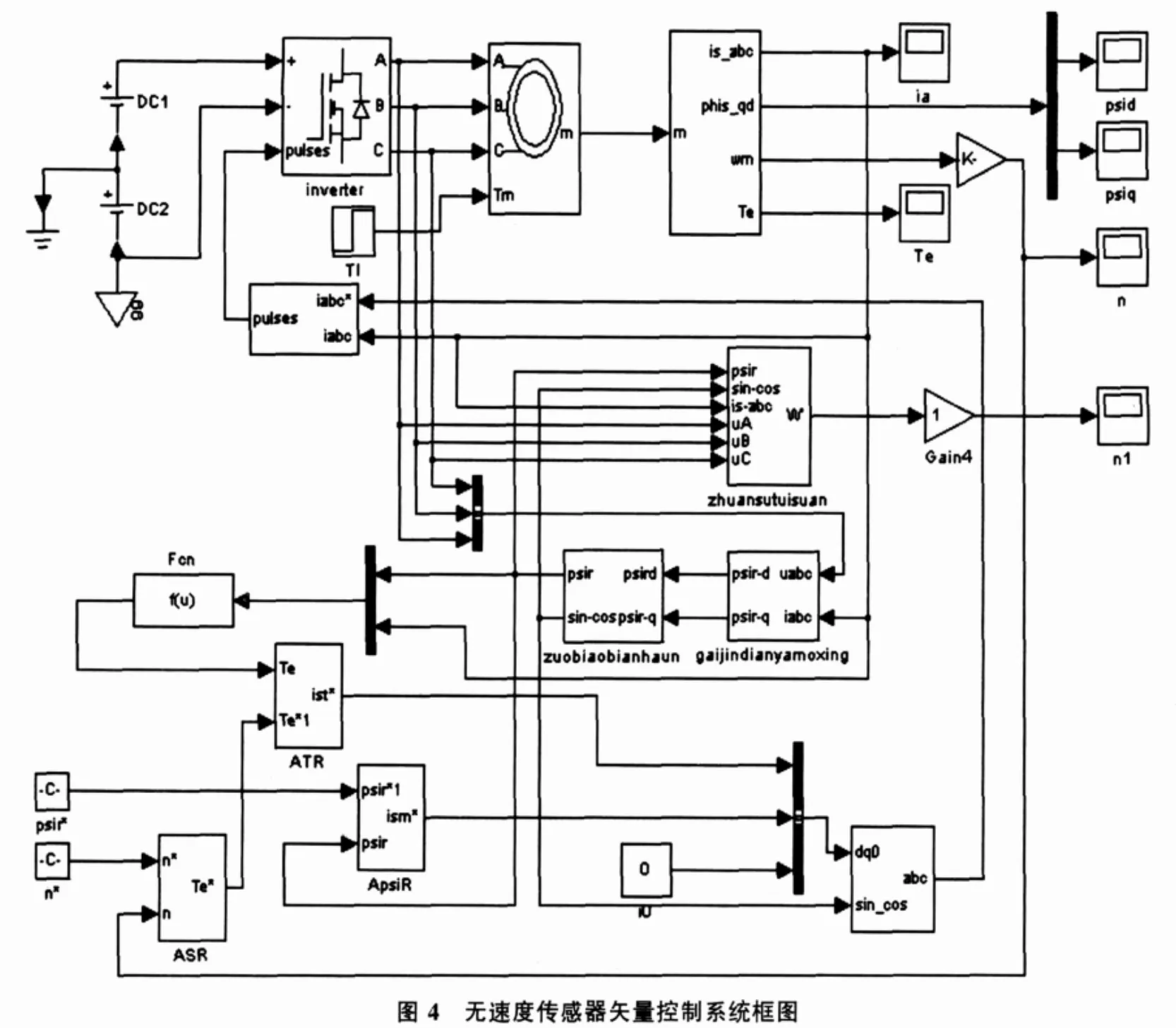
在Matlab/Simulink環境下，建立無速度傳感器變頻空調矢量控制仿真模型如圖4所示：

4.2 仿真波形與結果分析

系統仿真所用電機為Y接三相異步電動機，參數設定如下：額定電壓 380V，頻率50Hz，極對數 pn=2，轉動 慣 量 J=0.002kg/m2， 定 子 電 阻 Rs=0.384Ω，定子電感 Ls=0.002mH， 轉 子 電 阻Rr=0.836Ω，轉子電感Lr=0.002mH， 互 感Lm=0.0891mH。模型的仿真算法采用Ode23tb[5]，空載起動，在1.0s時突加額定負載，仿真時間設為2.5s。考慮到空調壓縮機

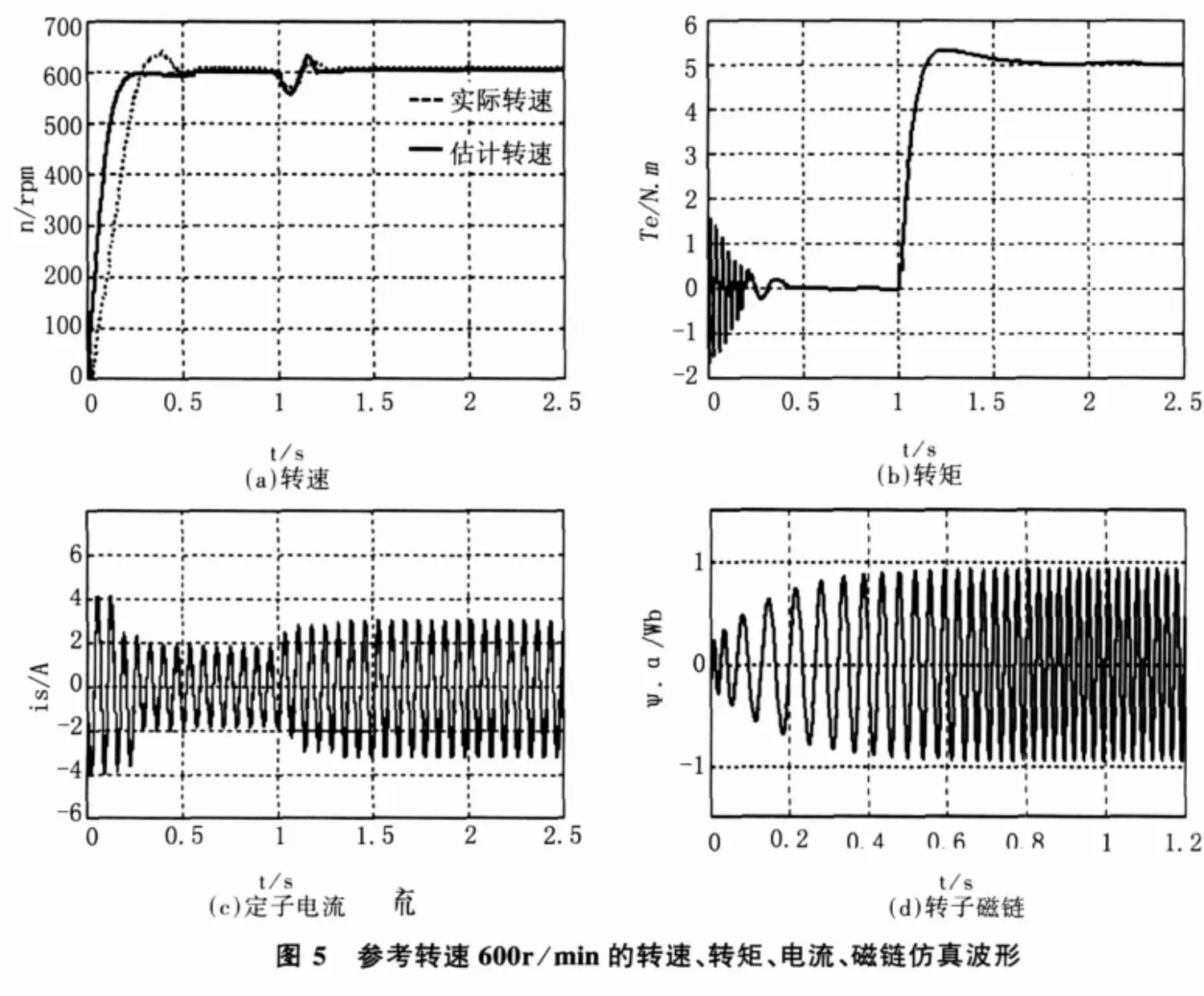
有最低頻率限制[1]，故設定參考轉速為600r/min進行仿真。轉速、轉矩、電流以及磁鏈的仿真波形如圖5所示：

圖5（a）所示轉速響應曲線表明，起動時轉速略有超調，由于PI調節器的影響，動態時估計轉速與實際轉速有一定的差異；但穩態時的速度辨識精度較高，0.5s以后估計轉速與實際轉速幾乎完全重合。圖 5（b）、（c）分別為轉矩、定子電流仿真波形，起動時轉矩及電流波動較大，但轉矩響應較快，穩態時 ，轉矩、電流的波動都很小。圖5（d）給出了轉子磁鏈α分量的仿真波形，由于改進了轉子磁鏈電壓模型中的純積分環節，磁鏈觀測較準確，從圖中可以看出，動態時轉子磁鏈波動小，幅值、相位穩定。

5 結論

本文通過改進電壓型轉子磁鏈觀測模型以及PI自適應速度辨識構建了變頻空調無速度傳感器矢量控制仿真模型。仿真結果表明：系統動態響應較快，穩態時的速度辨識精度高，磁鏈觀測準確。將無速度傳感器矢量控制應用于空調變頻控制系統，可降低壓縮機轉速波動，顯著減小震動及噪聲。

[1]石文星，彥啟森，陳華俊，王寶龍.論變頻空調性能評價體系[J].暖通空調，2004，34（5）：52 ～ 58.

[2]馮垛生，曾岳南.無速度傳感器矢量控制原理與實踐[M]第二版.北京：機械工業出版社，2006.

[3]李永東.交流電機數字控制系統[M].北京：機械工業出版社，2003.

[4]Young Ahn Kwon,Sung Hwan Kim,A New Scheme for Speed Sensorless Control of Induction Motor[J].IEEE Trans.On Industrial Electronics,2004,51（3）:545～550.

[5]洪乃剛.電力電子和電力拖動自動控制系統的MATLAB仿真[M].北京：機械工業出版社，2006.