基于新型變結構控制策略的直接轉矩控制系統研究

鄧國璋

黃岡職業技術學院

0 引言

直接轉矩控制（direct torque control，DTC）是上個世紀八十年代由德國魯爾大學的Depenbrock教授提出的一種高性能交流變頻調速技術，并成功應用于感應電機控制領域。直接轉矩控制技術放棄了矢量控制中電流解耦的控制思想，省略了電壓調制模塊和電流反饋環，通過檢測定子電壓和定子電流，直接計算出電機的磁鏈和轉矩，并采用兩個滯環比較器直接實現對定子磁鏈和轉矩的解耦控制，因此具有結構簡單、轉矩響應快、對系統內部參數攝動和外部干擾魯棒性強等優點，但同時也存在電流、磁鏈和轉矩脈動大，逆變器開關頻率不固定，系統低速運行時難以精確控制以及因轉矩脈動引起的高頻噪聲等問題[1]。很多研究[2]－[5]表明，將空間矢量調制技術與直接轉矩控制相結合可以有效解決DTC磁鏈和轉矩的波動，并且可以實現逆變器開關頻率恒定。然而在空間矢量轉矩控制系統中，速度控制一般采用PI調節器，其中比例系數越大系統響應速度越快，但同時也增加了系統對噪聲的敏感性，積分環節的主要作用是消除系統的穩態誤差，但存在積分飽和問題，容易對系統的穩定性造成不利的影響。同時其設計過程比較依賴于控制對象的數學模型，對非線性、強耦合對象的適應性較差，對系統參數、外部擾動缺乏魯棒性，因此在低速時很難達到較為理想的控制性能。

變結構控制（variable structure control，VSC）是一種魯棒性較強的非線性控制方法，具有結構簡單、響應快速、對系統參數攝動及外部擾動不敏感等優點。然而傳統變結構控制中離散化采樣延遲、開關器件慣性等因素容易導致“抖振”問題，引起高頻振蕩，對系統的控制性能造成很大危害。因此本文提出一種新型控制策略，將變結構和PI控制相結合，在變結構策略中采用帶有線性區間的非線性控制結構，既能利用非線性特性抵償內外擾的影響，又能實現系統在原點附近無抖振，在保證變結構控制快速性和魯棒性優點的同時，有效改善了系統的性能。

1 感應電機直接轉矩控制

感應電機直接轉矩控制系統的結構如圖1所示，磁鏈環和轉矩環均采用滯環調節器，根據調節器的輸出通過開關向量表選擇合適的電壓矢量，對磁鏈和轉矩進行控制。圖中定子磁鏈可由如下表達式計算:

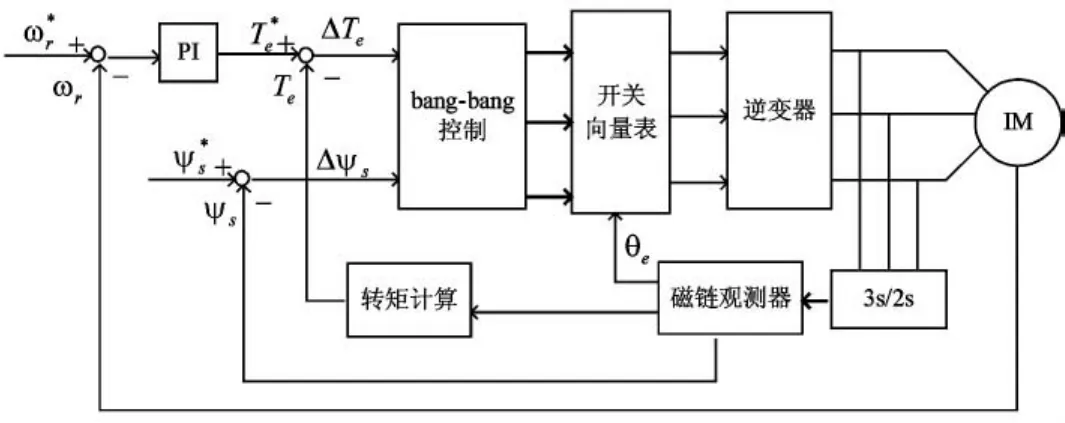
圖1 感應電機直接轉矩控制系統結構框圖

式中 ψs、Vs和Is分別為定子磁鏈、定子電壓和定子電流，Rs為定子電阻。

在靜止兩相坐標系下，電磁轉矩Te可由式（2）計算:

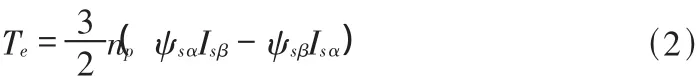
其中 ψsα，ψsβ分別為定子磁鏈的 α， β 分量，Isα， ψsβ分別為定子電流的 α，β分量，np為電機極對數。

2 基于VSC的空間矢量直接轉矩控制

基于變結構控制的空間矢量直接轉矩控制系統的原理如圖2所示。轉速給定值ω＊r與反饋值 ωr之差經過速度環控制器，得到電磁轉矩的給定信號。由轉矩觀測值Te與相比較得到轉矩誤差信號ΔTe，經過PI調節器，再與 ωeψs相加生成定子電壓分量。由定子磁鏈觀測值 ψs與定子磁鏈給定信號相比較得到磁鏈誤差信號Δψs，再經過PI生成定子電壓分量，然后結合定子磁鏈位置角 θψs進行坐標變換，從而產生SVM模塊的輸入電壓指令和，最后由SVM的輸出控制逆變器的開關信號。圖中速度環控制器的結構如圖3所示。下面將對速度環控制策略的設計進行具體分析。

其中Te為電磁轉矩，TL為負載轉矩，np為轉子極對數，J為轉動慣量，ωr為電氣角速度，B為摩擦系數，則速度環的跟蹤誤差:

對圖3所示的控制器，其控制量:

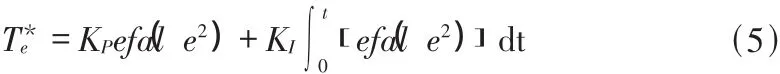
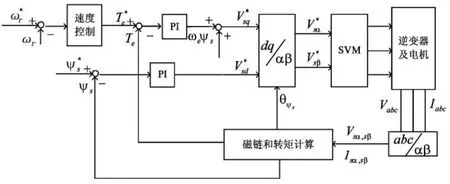
圖2 基于VSC的空間矢量直接轉矩控制系統結構框圖

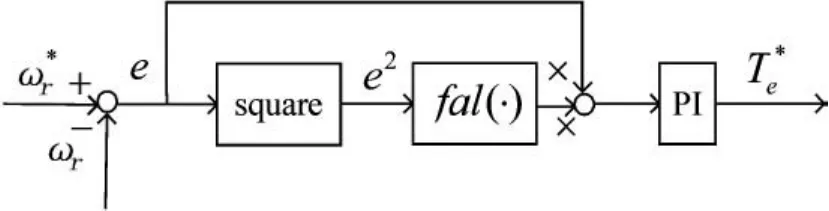
圖3 速度環控制器結構圖

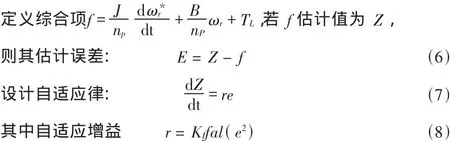
帶有線性區間的非線性fal函數定義如下

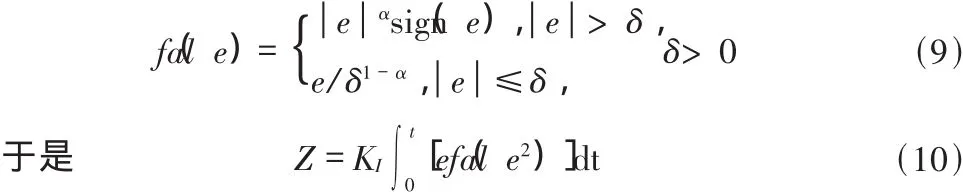
為了保證Z對f觀測誤差的有界性，本文引入不連續投影算子[6]對自適應律加以修正:

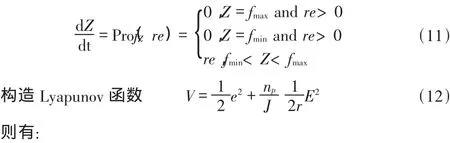
因此對圖2中的直接轉矩控制系統，若采用圖3所示的控制器，以及式（7）～（11）描述的自適應律，則系統全局一致漸近有界。

3 仿真實驗分析

為了驗證本文提出控制策略的有效性，應用Matlab/Simulink對圖2和圖3所示系統進行了仿真實驗，并將仿真結果進行了對比。仿真時所用的感應電機參數如下:

額定功率:5.5kW 額定電壓:380V

額定頻率:50Hz 極對數:2

定子電阻:0.813Ω 轉子電阻:0.531Ω

定子電感:0.10626H 轉子電感:0.10875H

勵磁電感:0.1024H 轉動慣量:0.02kg·m2

圖1滯環控制器的容差范圍設為0.001。電機起動時給定轉速設為0轉/分，0.2秒時電機轉速變為150轉/分，0.5秒給系統突加TL=35N·m的額定負載，仿真結果如圖5至圖7所示。

圖4和圖5為直接轉矩控制系統和基于VSC的空間矢量直接轉矩控制系統的轉矩響應曲線及其局部放大圖。從圖中可以看出，這兩種系統的轉矩動態響應速度沒有明顯差異，直接轉矩控制系統的轉矩波動范圍為±2N·m，基于VSC的空間矢量直接轉矩控制系統的轉矩脈動為±1N·m，大約減小了50%。圖6為系統的轉速響應曲線，由圖可知轉速突變和突加負載時，直接轉矩控制系統的轉速波動較大，到達穩態的時間較長，而基于VSC的空間矢量直接轉矩控制系統轉速響應較快，超調較小，加載后的恢復時間較短，表明本文提出的控制策略在改善了系統性能的同時有效解決了抖振問題，

5 結論

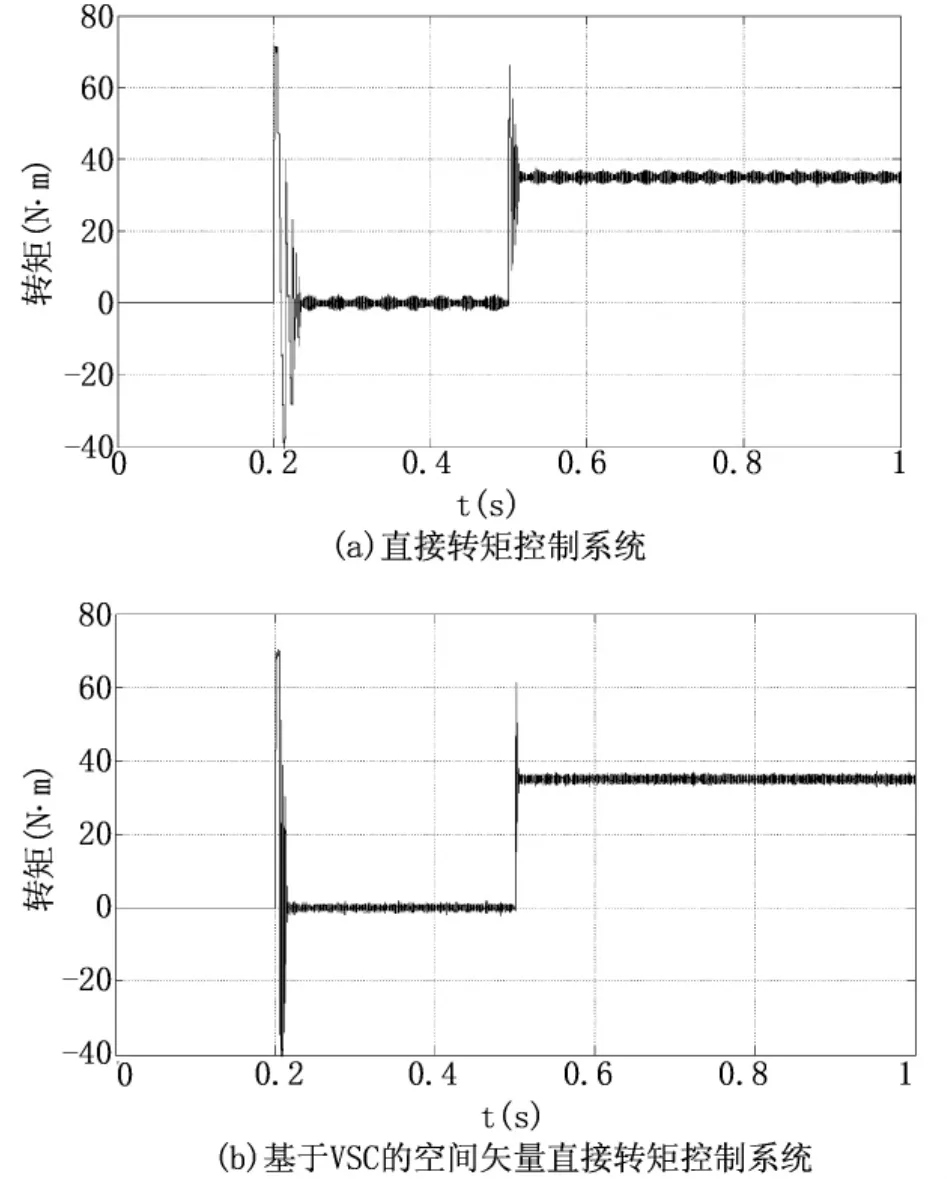
圖4 轉矩響應

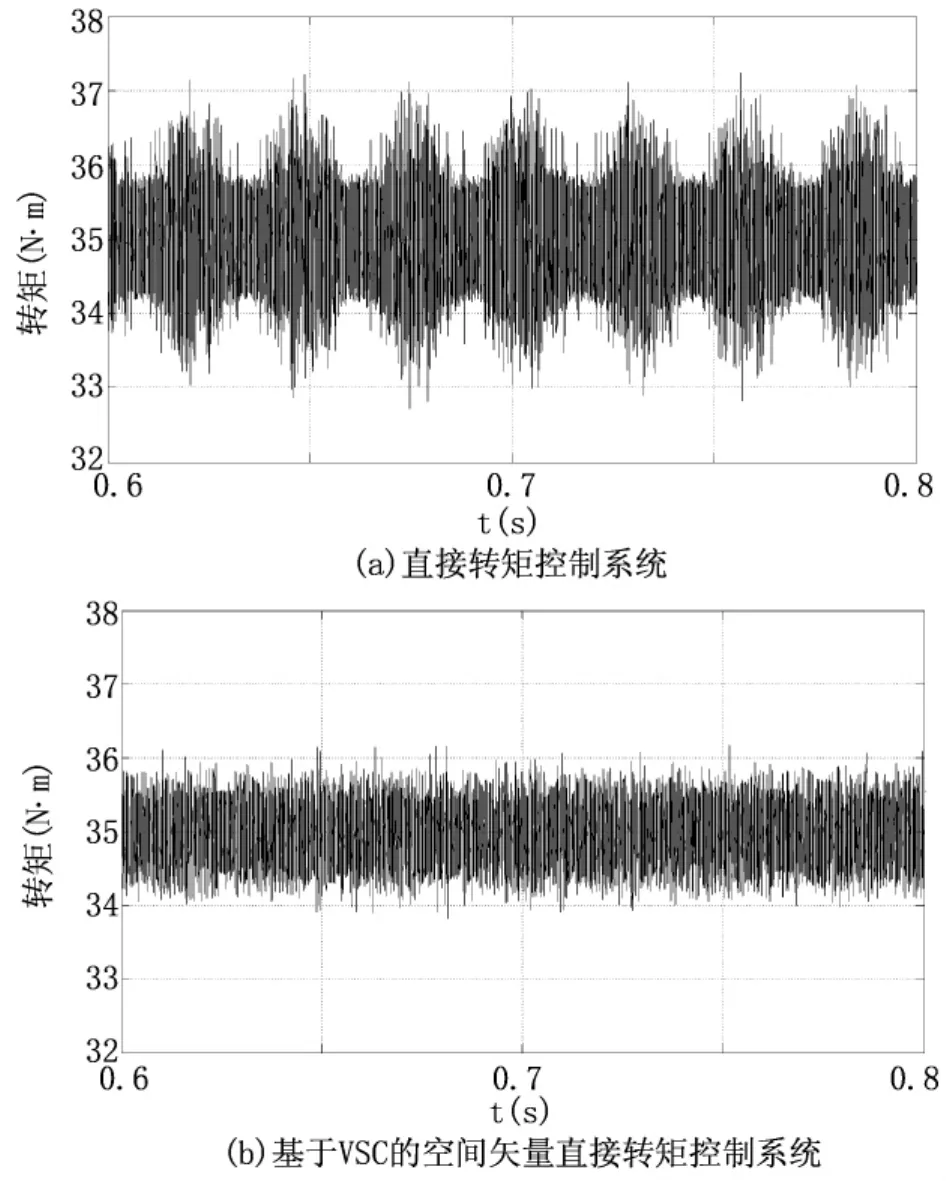
圖5 轉矩響應局部放大圖

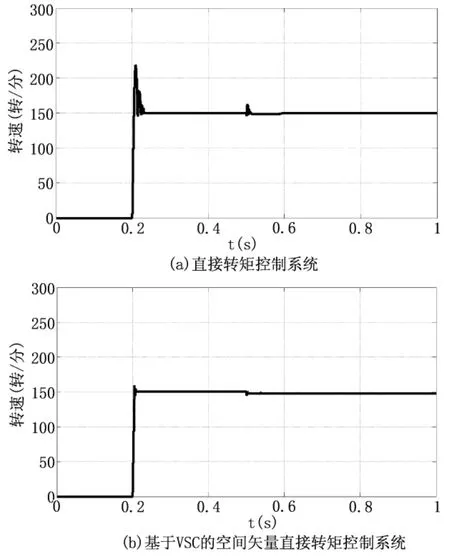
圖6 轉速響應

針對感應電機直接轉矩控制系統磁鏈和轉矩波動大、逆變器開關頻率不固定等問題，本文提出一種新型控制策略，在變結構控制中采用帶有線性區間的非線性控制結構，保證變結構控制快速性和魯棒性的同時，又能實現系統在原點附近無抖振，有效改善了系統的動態和穩態性能，具有一定的理論和實用價值。

[1]賈洪平，孫丹，賀益康.基于滑模變結構的永磁同步電機直接轉矩控制[J].中國電機工程學報，2006，26（20）:134 ～ 138.

[2]Lai Y.S.， Chen J.H.A new approach to direct torque control of induction motor drives for constant inverter switching frequency and torque ripple reduction[J].IEEE Transactions on Energy Conversion.2001，16（3）:220 ～227.

[3]Lascu C.，Boldea I.， Blaabjerg F.Very-low-speed variable-structure control of sensorless induction machine drives without signal injection[J].IEEE Transactions on Industry Applications.2005，41（2）:591 ～ 598.

[4]Zelechowski M.，Kazmierkowski M.P.，Blaabjerg F.Controller design for direct torque controlled space vector modulated（DTC－SVM）induction motor drives[J].Proceeding of Power Electronics and Drive Systems，2005，951～956.

[5]Shady M.Gadoue，Damian Giaouris and John W.Finch.Sensorless Control of Induction Motor Drives at Very Low and Zero Speeds Using Neural Network Flux Observers[J].IEEE Transactions on Industrial Electronics，2009，56（8）:3029～3039.

[6]Sastry S.，Bodson M.Adaptive Control-Stability Convergence and Robustness[M].New Jersey:Prentice Hall， 1989:58 ～ 65.

[7]Loannou P.， Fidan B.Adaptive Control Tutorial[M].Philadelphia:Society for Industrial and Applied Mathematics， 2006:52～63.