螺旋槳目標的雷達回波信號相位解纏技術

姜 巖,陳筠力,王 赟

(上海衛星工程研究所,上海 200240)

0 引言

螺旋槳對雷達回波會產生周期性的調制效應。BELL,GRUBBS等建立了噴氣式飛機引擎螺旋槳調制效應的數學模型,并由此獲得了螺旋槳回波包絡的規律[1]。MARTIN,MULGREW對直升機、螺旋槳飛機和噴氣式飛機的螺旋槳或旋轉引擎的雷達回波頻譜進行了特征提取,進而對三類目標進行分類[2、3]。丁建江、張賢達等對基于螺旋槳特征提取的目標識別在防空系統中的應用作了研究[4]。由于從回波頻譜中可得目標的周期特征等信息,致使通過研究相位獲取目標信息被忽視了。螺旋槳雷達回波相位中含目標的速度、目標螺旋槳的周期特征,以及螺旋槳類型特征等豐富的目標信息,因此研究相位的變化規律對目標識別、多普勒估計,以及螺旋槳飛機成像去干擾均有重要意義。眾所周知,雷達接收機常利用正交雙通道接收回波。接收機的基帶輸出是以脈沖重復頻率為抽樣頻率的抽樣值,包括I通道和Q(正交)通道的輸出。信號中包括的幅值信息不會發生大的變化,但用普通方法求其相位只能得到(0,2π)間的值,即相位的主值,因此需利用某種相位解纏技術將其展開。目前,較常用的相位解纏技術有數值積分算法、SCHAFER的門限算法和TRIBOLET的自適應數值積分算法[5、6]。其中,SCHAFER的算法利用相位主值的跳變將其展開再還原成實際相位,另兩種算法均利用相位梯度積分方法還原實際相位。實驗表明,槳葉數為奇數和偶數時螺旋槳的雷達回波相位差異非常大。槳葉為奇數時回波相位光滑,適于用積分方式展開,槳葉為偶數時回波相位跳變很大,適于門限算法展開。

螺旋槳回波信號的離散性是形成相位混疊效應的主要原因,而相位解纏技術又受脈沖重復頻率過低、飛機飛行速度過大,以及回波相位帶寬過大等因素的制約。本文基于經典螺旋槳回波調制模型,研究了螺旋槳雷達回波調制模型的相位解纏技術。

1 螺旋槳雷達回波相位調制模型

1.1 基本回波模型建立

為研究螺旋槳雷達回波的相位在相對運動中的變化規律,建立雷達與螺旋槳相對運動坐標系如圖1所示。建模中,省略飛機部分直接給出螺旋槳的結構。設螺旋槳相對雷達以速度v作徑向運動,同時以角速度ωp轉動;在時刻t,螺旋槳中心相對雷達的距離為R(t);雷達視角即雷達視線與螺旋槳旋轉平面的夾角為β。同時建立螺旋槳自身坐標系：螺旋槳旋轉平面位于平面XOY(為便于分析,取平面XOY平行于地平面);忽略槳葉螺距角的影響,每個槳葉根部至螺旋槳中心的距離為a,尖端至螺旋槳中心的距離為b,各槳葉形狀相同且槳葉間夾角一致。建立回波信號模型所需參數有：雷達與螺旋槳坐標系中心的初始距離R0;R(t)=R0+vt;雷達載波頻率f0;雷達載波波長λ;光速c;螺旋槳旋轉頻率fp;單個螺旋槳的葉片數N。

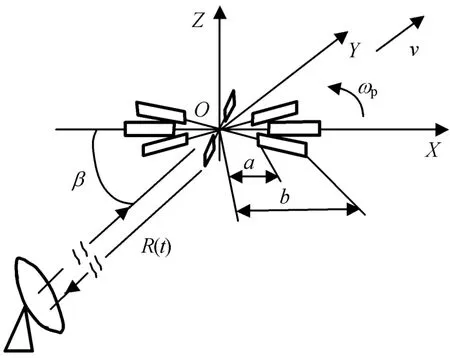
圖1 雷達與螺旋槳相對運動Fig.1 Relative motion between radar and propeller

電磁波波長遠小于螺旋槳,故可認為雷達的后向散射工作于光學區。則,假設每個螺旋槳葉片均是一強散射中心,N個葉片螺旋槳的雷達回波就可視作N個散射中心的雷達回波的疊加。當不考慮雷達天線掃描形式和螺旋槳葉片螺距角的影響時,螺旋槳的雷達回波可表示為

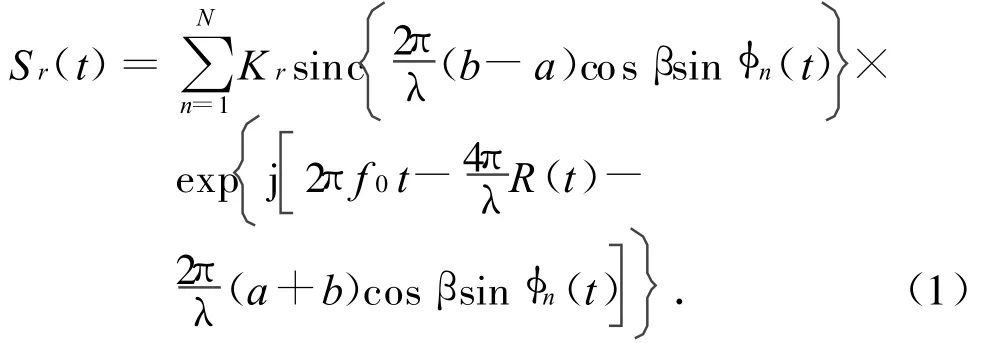
由于載波和初始距離R0對螺旋槳特性的影響較小,且載波的接收亦采用相干方式,可簡化公式,去掉相位中的2πf0t項和由R0引起的項,剩余部分用Sb(t)表示,即

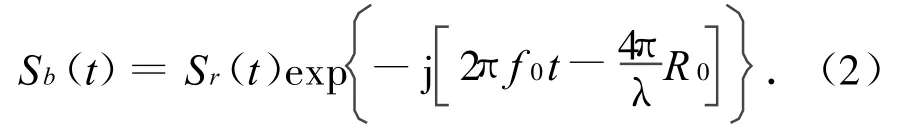
代入式(1),得

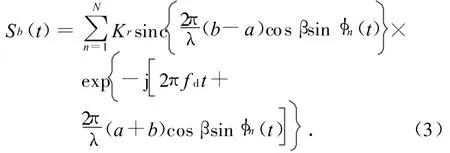
式中：fd為多普勒頻率,且fd=2v/λ。

由式(3)可知：對單個螺旋槳葉片來說,其雷達回波復包絡的幅度部分為周期出現的辛格脈沖函數,該周期與螺旋槳的旋轉周期相關,而回波復包絡的相位部分為一條以多普勒頻率為斜率的直線疊加一正弦周期變化的波動,周期變化規律與幅值相似。

1.2 回波相位特性分析

當飛機距離雷達很遠,且飛機平穩飛行時,可認為fd,β近似不變。這樣,對單個螺旋槳葉片來說,就可提取其相位因子。設相位部分

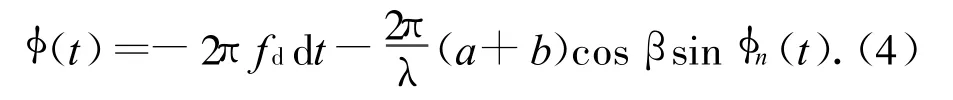
為得到該項的變化規律,選定一組參數進行仿真。

仿真1：設雷達波長3 cm,脈沖重復周期0.1 ms,螺旋槳槳葉長1.2 m,fp=50 Hz,螺旋槳相對雷達運動速度30 m/s,式(4)的仿真結果如圖2所示。由圖可知：單葉螺旋槳轉動引起的正弦波動因多普勒斜率被向下拉長,這與式(3)模型吻合。

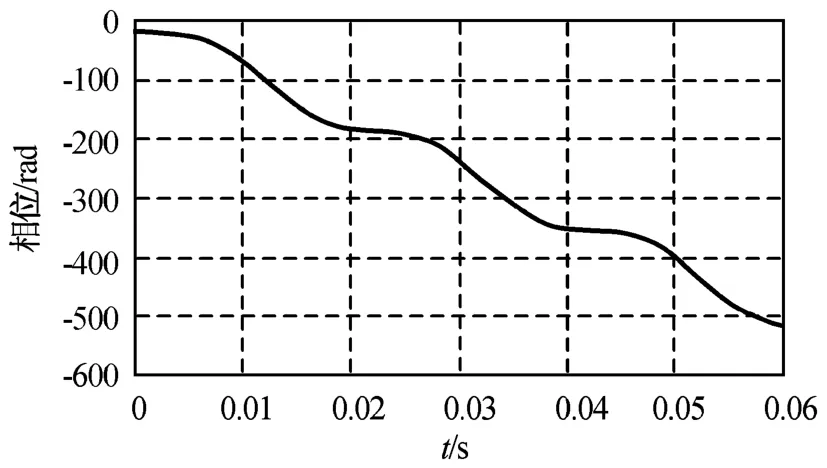
圖2 螺旋槳回波模型相位因子Fig.2 Phase of MMBM

實際的螺旋槳至少有2個葉片,渦扇發動機的扇葉甚至有數十個,因此多槳葉螺旋槳回波的相位是本文研究的重點。本文基于式(1)模型,通過改變公式以理解和分析相位的調制特征。理論研究相位結構,需分析N分別為奇數和偶數兩種狀況。

當N為偶數時(假設N=4,其他N類似),由式(3)可知：螺旋槳上角度相差π的兩葉片的回波復包絡的幅值(辛格函數)也相差π,即相當于這兩項的幅度一樣,可將其作疊加合并。對式(3)作變形,分別對n=1,3和n=2,4進行合并,其和式分別為S1,3(t),S2,4(t),則

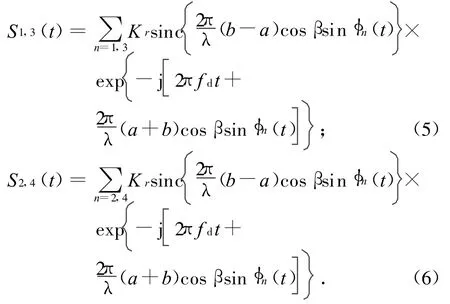
為便于合并,設φn0(t)=2πfpt+φ0,βr1=(ba)cosβ,βr2=(b+a)cosβ,則式(5)、(6)合并后為

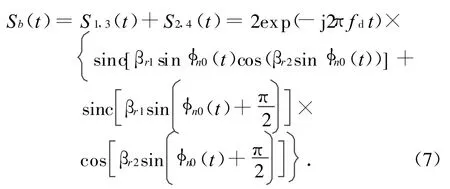
實際上對多數螺旋槳和渦扇來說,槳葉或扇葉的根部均與旋轉中心直接相連,即a=0,相當于βr1=βr2。則,式(7)可進一步簡化為

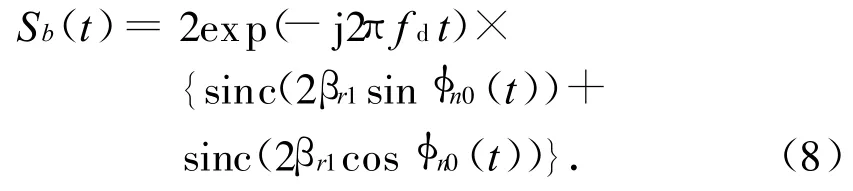
由式(8)可知：其相位由兩部分構成。第一部分是以fd為斜率隨時間變化的斜線;第二部分由2個實辛格函數組成,相位只能是0或π。因此,偶數片槳葉的雷達回波能使相位上的正弦波動相互抵消。

仿真2：取N=4,其他參數與仿真1相同,仿真結果如圖3所示。

圖3 改進模型的螺旋槳回波相位(N=4)Fig.3 Phaseof updated model(N=4)

同理,當N為其他偶數時,同樣可得回波模型的簡化形式為

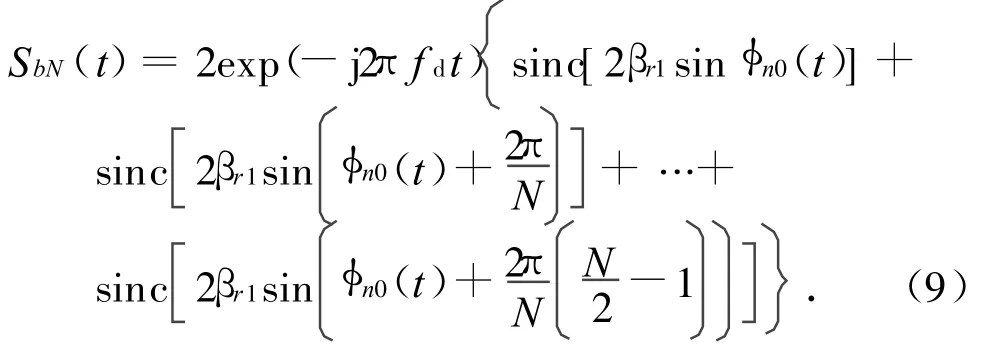
由式(9)可知：除項數增加外,它與式(8)并無大的區別,故其相位亦與式(8)相似,均是以fd為斜率的隨時間變化的斜線疊加幅值為π的辛格脈沖函數。

當N為奇數時,螺旋槳各葉片的回波不能合并,槳葉分布的不對稱性不能消除回波相位的波動。實際上,奇數片槳葉雷達回波的相位分布與圖2相所示的那樣分布相似,但N不同會使波動的周期性各異。

2 回波調制模型相位混疊效應分析

2.1 相位混疊效應產生原因

雖然理論相位可由模型而得,但雷達回波的相位不可能直接獲得,通常是用正交雙通道技術對回波進行相干解調并獲得回波復包絡的實部I(n)和虛部Q(n)(正交通道)的離散抽樣值,其抽樣頻率即為脈沖重復頻率。因此,實際的螺旋槳雷達回波與式(3)不同。用Sb(n)表示回波,則

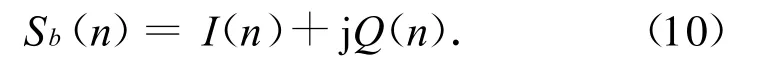
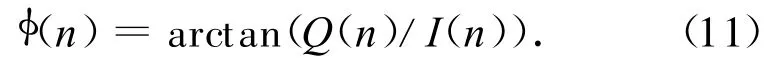
φ(n)的主值取值范圍為(-π,π)。

仿真3：取N分別為1,4,其他參數不變,按式(11)對回波相位進行仿真,結果如圖4所示。由圖可知：相位丟失了原來的規律性,且槳葉數越多,波形就越混亂。相位模糊主要緣于雷達回波的離散性。飛機的飛行速度越大、重復頻率越低,回波相位的跳變就越大,相位解纏實施也越難,另外主值相位的大帶寬增大了相位解纏的難度。

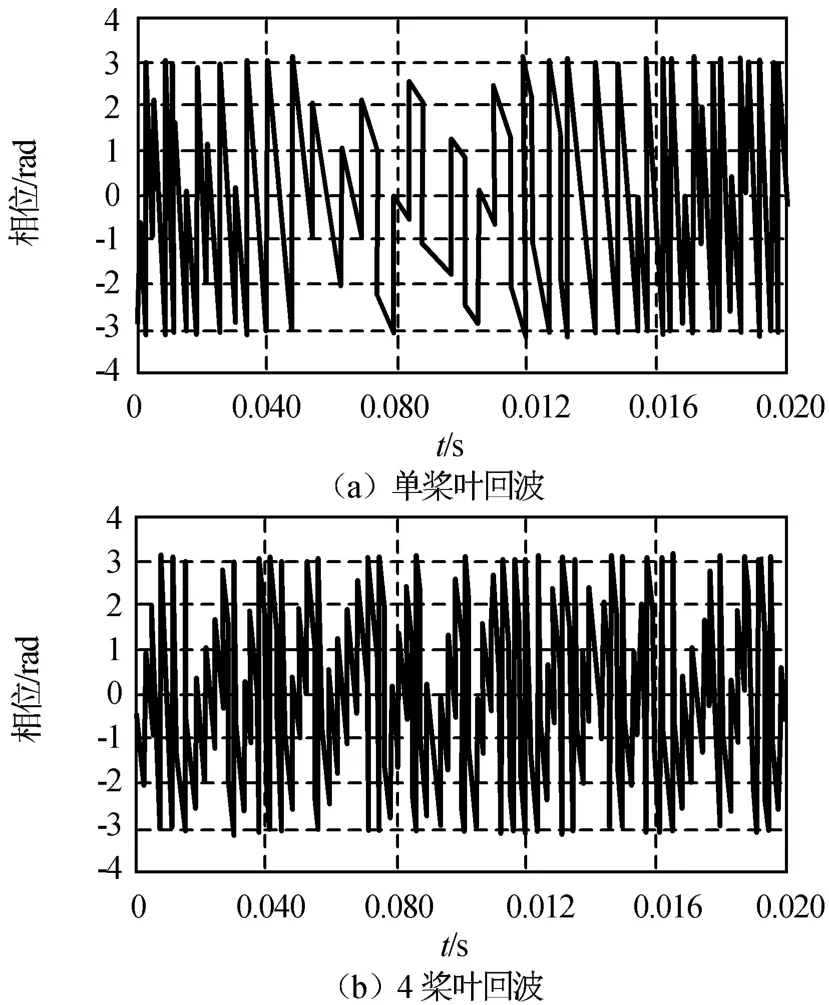
圖4 不同時間的螺旋槳回波相位Fig.4 Propeller phaseunder different time

2.2 兩種相位解纏方法在螺旋槳雷達回波相位解纏中的應用

針對槳葉數為奇數和偶數時雷達回波相位的特點,本文提出兩種相位解纏算法：TRIBOLET的自適應數值積分算法和插值與可調門限相結合的算法。第一種算法根據相位函數的變化快慢自適應調整步長,對相位梯度進行梯形積分實現解纏,但當相位有劇烈跳變或連續性很差時該算法即不再適用,故它適于槳葉數為奇數時的相位解纏。第二種算法適于相位連續性較差變化劇烈狀況,可通過相位插值和調整門限減少錯誤解纏,較適于槳葉為偶數時的相位解纏。

2.2.1 TRIBOLET自適應數值積分算法

設arg Sb(n)為螺旋槳的雷達回波信號的相位主值。若其真實值為φ(n),則時刻n的相位真實值

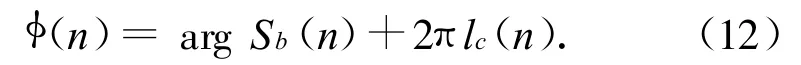
式中：lc(n)為指φ(n)與arg Sb(n)相差lc(n)個2π。只要求出lc(n),相位解纏即完成。

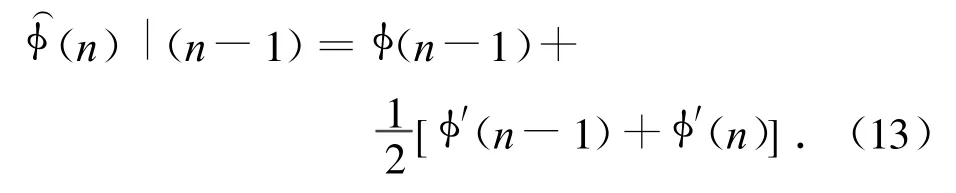
其中,φ′(n)可根據反正切函數求導,即

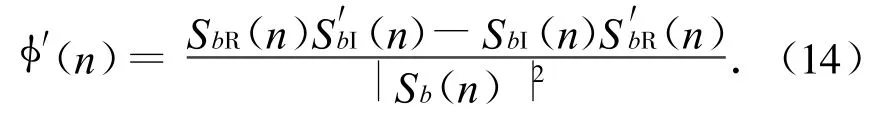
式中：下標R,I分別表示函數的實部和虛部。

因使用了相位的導數,要求原相位函數連續光滑。通過插值合理調整積分步長就可滿足

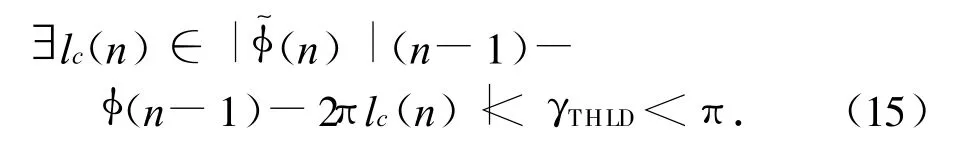
式中：γTHLD為相位中相鄰兩點的差值。該算法的核心是根據函數變化的快慢自適應地調整步長,在變化劇烈處適當插值縮短步長,相對平滑處增加步長,當誤差小于設定的門限(γTHLD)即完成估計,γTHLD的大小取決于應用對精度的要求。此方法最后獲得對相位的一致估計,完成相位解纏。

2.2.2 插值與可調門限相結合算法

此算法的核心是先對回波作插值處理,再對插值所得主值相位相鄰的兩點的值進行判斷,當這個差值超過門限時,對后面的相位作2π補償。算法的判斷公式為

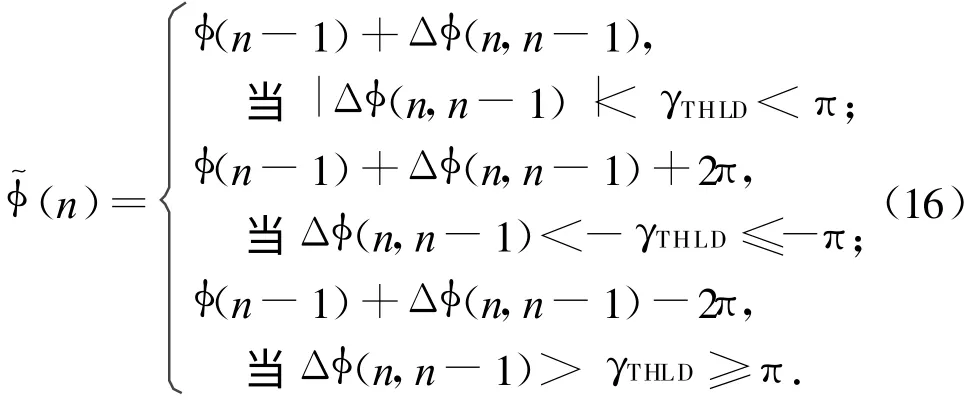
式中：Δφ(n,n-1)為主值相位差,且Δφ(n,n-1)=arg Sb(n)-arg Sb(n-1)。

該算法受采樣率的影響較大,采樣率不足時應盡量對回波信號進行插值處理,再提取相位主值進行解纏。

3 仿真

設雷達波長0.43 m,雷達發射25.6μs的矩形脈沖,脈沖重復周期0.1 ms,飛機飛行徑向速度30 m/s,雷達視角30°,螺旋槳槳葉參數a=0 m,b=1.2 m,f p=50 Hz。N分別為2,4,12時,插值與可調門限相結合算法所得相位解纏結果分別為圖5～7所示。由圖可知：相位可近似視作有一定間隔的幅度π的脈沖疊加于一條斜線上,與式(9)吻合。槳葉空間位置的對稱性使角度相差π的每對槳葉的回波能相干疊加,致使相位出現幅值為π的跳變。由圖可得斜線的斜率為-875 rad/s,與由2πfd而得的理論值-876.7 rad/s基本相符。同時,相位呈現一定的螺旋槳周期調制特征,圖5每隔9個脈沖為1個周期,0.02 s內共有2個周期,而螺旋槳的調制周期為0.02 s,槳葉數為2;圖6每隔6個脈沖為1個周期,槳葉數為4;圖7每隔2個脈沖為1個周期,槳葉數為12,表明相位的調制周期為螺旋槳調制周期的1/N。N分別為3,5,15時,自適應數值積分算法所得相位解纏結果分別如圖8～10所示。與N為偶數相比,N為奇數時經解纏的相位顯更平滑,且周期性更明顯,槳葉數越多,相位的波動就越接近正弦波形。螺旋槳調制周期為0.02 s,圖8～10的相位的周期分別為螺旋槳調制周期的1/3,1/5,1/15。因此,其周期性質與N為偶數時一致。

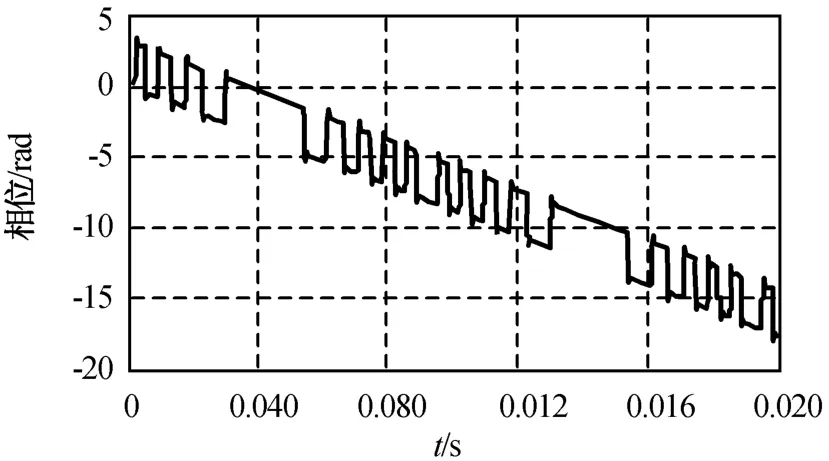
圖5 用插值與可調門限相結合算法解纏后相位(N=2)Fig.5 Phase after phase-unwrapping achieved by arithmetic of interpolation and adaptive threshold(N=2)

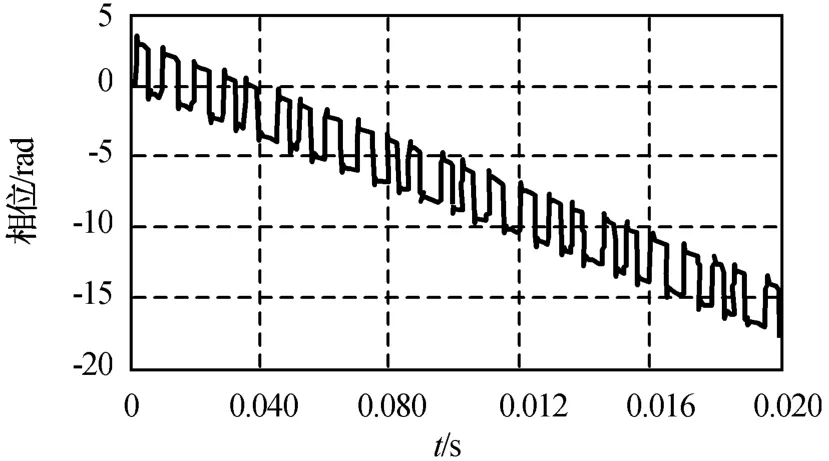
圖6 用插值與可調門限相結合算法解纏后相位(N=4)Fig.6 Phase after phase-unwrapping achieved by arithmetic of interpolation and adaptive threshold(N=4)

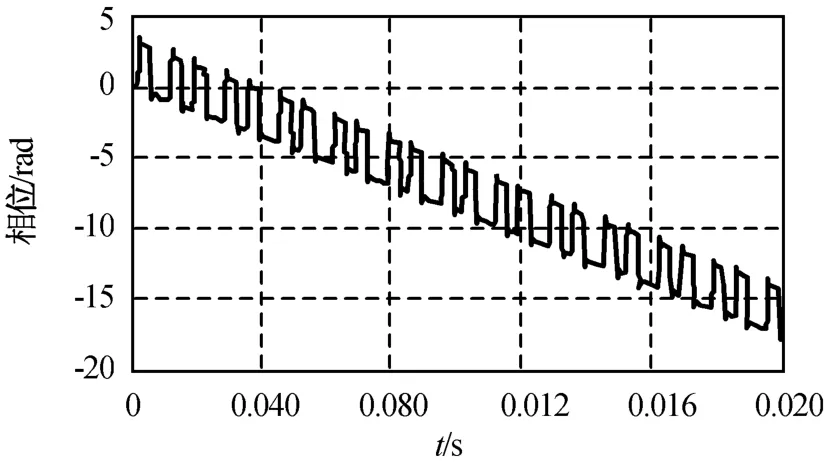
圖7 用插值與可調門限相結合算法解纏后相位(N=12)Fig.7 Phase after phase-unwrapping achieved by arithmetic of interpolation and adaptive threshold(N=12)

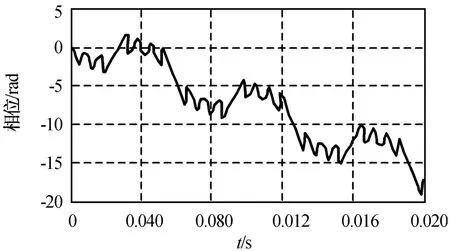
圖8 用自適應數值積分算法解纏后相位(N=3)Fig.8 Phase after phase-unwrapping achieved by arithmetic of self-adaptive numerical integration(N=3)

4 結束語

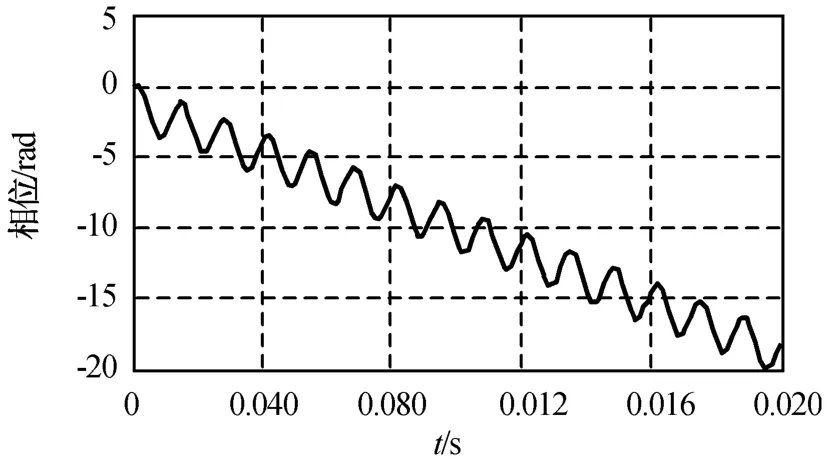
圖10 用自適應數值積分算法解纏后相位(N=15)Fig.10 Phaseafter phase-unwrapping achieved by arithmetic of self-adaptive numerical integration(N=15)

本文建立了螺旋槳雷達回波信號的模型,對模型回波信號的相位混疊效應進行了理論分析,推導了槳葉數為偶數時回波模型的改進形式,分析了螺旋槳調制模型中雷達回波的相位理論值。討論了螺旋槳回波相位出現模糊的原因,并據此提出了插值與可調門限相結合的算法和自適應數值積分算法兩種算法分別在槳葉數為奇數和偶數時進行相位解纏,結果較理想,由解纏后相位圖對多普勒頻率和螺旋槳調制周期估計的精度也較好。對螺旋槳相位的特征的研究可用于目標的識別和分析,是對基于頻譜分析的目標識別的重要補充。方法有較好的應用前景。

[1]CHEN V C.Radar signatures of rotor blades[C]//International Society for Optical Engineering.Washington D.C.：SPIE,2001：63-70.

[2]BELL M R,GRUBBS R A.JEM modeling and measurement for radar target identification[J].IEEE Trans.On AES,1993,29(1)：73-87.

[3]MARTIN J,M ULGREW B.Analysis of the theoretical return signal from aircraf t blades[C]//Proceedings of IEEE International Conference on Radar 1990.Washington D.C.：IEEE,1990：569-572.

[4]DING J J,YU Z Q,YAN D Z,et al.Modeling and validation of modulated characteristics for aircraft rotating structure in the air surveillance radars：IEEE International Radar Conference[C].IEEE,2005：641-646.

[5]OPPENHEIM A V,SCHAFER R W.Digital signal processing[M].Englewood Cliffs,NJ：Prentice-Hall,1995.

[6]TRIBOLET J. A new phase unwrapping algorithm[J].IEEE Transactions on Signal Processing,1977,25(2)：170-177.