一種基于信息融合的深空巡航段自主導航算法

常曉華,崔平遠,崔祜濤

(哈爾濱工業大學 深空探測基礎研究中心,黑龍江 哈爾濱 150080)

0 引言

自主導航技術能減少操作的復雜性,增強探測器的自主生存能力,并為姿態控制、機動規劃和軌道控制等自主能力提供支持,擴展探測器的空間應用潛力,因此逐漸成為深空探測任務的研究熱點。光學導航是深空探測中廣泛采用的一種自主導航方式,先后在Mariner系列、Viking任務、Galileo探測器、Stardust任務和Deep Space 1任務中進行了驗證,并成功應用于Deep Impact,SMART-1,MUSES-C等深空探測任務[1～4]。由國外探測任務可知,自主光學導航方法主要用于深空接近交會段、繞飛段和下降著陸段。文獻[5]研究了基于地月信息的自主光學導航方法在分離段中的應用。對自主光學導航方法在巡航段中的應用,其主要限制是缺乏足夠星歷精確的可見參考目標,從而影響了導航系統的軌道確定精度。

考慮小行星的數量和空間分布的緊密性,美國JPL實驗室的BHASKARAN等針對Deep Space 1任務研究了以小行星作為導航信標的深空巡航段光學導航方法[6]。在任務實施前,地面操控中心根據該任務的軌道特點,綜合視星等、太陽相角、視運動、三星概率、探測器與小行星距離和視線夾角等選取標準,對小行星進行規劃和篩選,獲得不同軌道段內的最佳觀測方案,并更新相應信標小行星的星歷信息。不同的任務軌道,小行星觀測方案各異。若飛行軌道發生改變,則需重新篩選導航小行星。

在深空探測的巡航段尤其是巡航段初期,考慮小行星的篩選準則和導航相機的拍照序列規劃,致使可用于導航系統的小行星圖像信息不一定滿足任務要求[7]。另外,對更遙遠的外太陽系探測等深空探測任務,地面站觀測獲得的小行星星歷信息誤差較大,且在任務實施之前難以對其進行更新,從而無法獲得符合軌道要求的小行星觀測方案。可見,自主光學導航方法在深空巡航段中的應用還需進一步的研究。

對深空探測的行星際巡航段,太陽是最穩定也是最重要的參考天體。文獻[8]研究了以太陽視線矢量為觀測量的自主導航方法,并用解析法分析了太陽視線矢量對導航參數的可觀測性,但因僅使用太陽視線信息,自主導航系統的可觀測度較低,導航精度不高,單純依賴太陽視線矢量的導航方法并不可行。

為此,針對深空探測巡航段的軌道確定,本文對一種基于信息融合的深空巡航段自主導航算法進行了研究。

1 狀態方程

在日心慣性坐標系中,深空探測器的軌道動力學模型可表示為

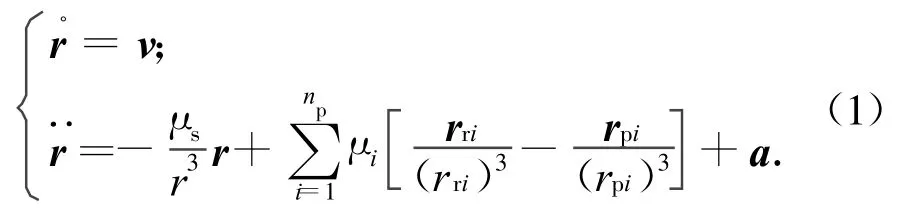
式中：r,v分別為日心慣性系內探測器的位置和速度,且r=‖r‖,r=[x y z]T,;μs為太陽引力常數;μi為第i個攝動行星引力常數;rpi為日心慣性系內第i個攝動行星的位置矢量;rri為第i個攝動行星相對探測器的位置矢量,且rri=rp i-r;np為攝動行星數,取np=6;a為未建模的攝動加速度矢量。

選取狀態變量X=[rTvT]T,根據軌道動力學模型可得導航系統的狀態方程為

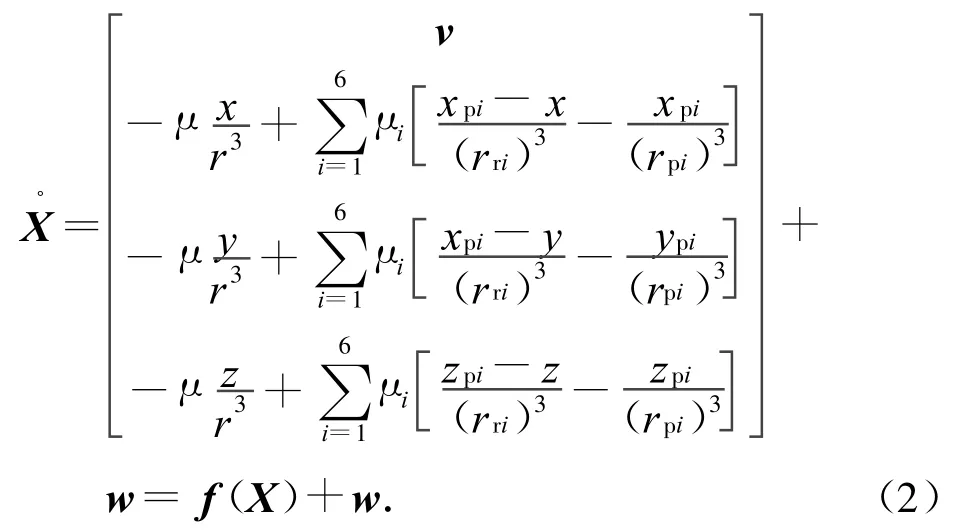
式中：w為系統模型誤差;X為系統狀態。

2 觀測方程

利用太陽敏感器測量太陽相對探測器的視線矢量,同時利用分光計進行單程多普勒測量,從而獲得探測器相對太陽的徑向速度,其觀測模型如圖1所示。圖中：ls為太陽相對于探測器的視線矢量;vr為探測器相對太陽的徑向速度。測量過程中,所有姿態信息均由姿態控制系統提供。

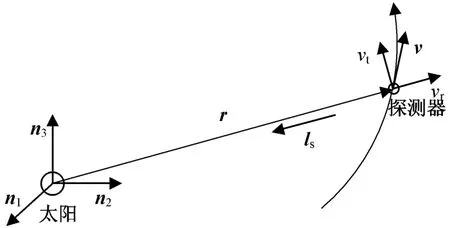
圖1 導航系統觀測模型Fig.1 Observation model of navigation system

2.1 太陽矢量觀測方程

現代高精度太陽敏感器多采用電荷耦合器件(CCD),如Solar-A探測器采用的高精度CCD太陽敏感器,測量精度為0.001°;俄羅斯地球物理協會(Geofizika)研制的視場為92°×92°的CCD太陽敏感器,其測量精度為角秒級[9]。

如圖1所示,太陽視線矢量的觀測模型為

考慮太陽敏感器的測量誤差時,可得太陽矢量的觀測方程為

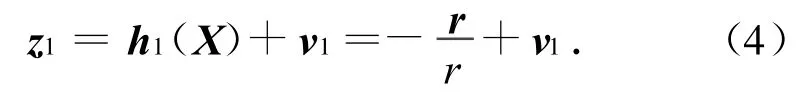
式中：v1為太陽視線矢量的觀測噪聲,假設其為零均值高斯白噪聲。

2.2 徑向速度觀測方程

通過分光計測量探測器相對太陽運動產生多普勒頻移,可得日心慣性系中探測器的徑向速度

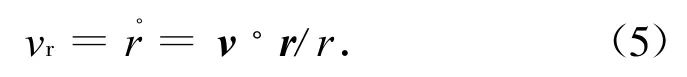
考慮測量誤差時,徑向速度的觀測方程為

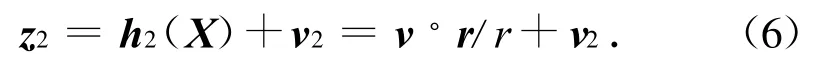
式中：v2為徑向速度的觀測噪聲,取其為零均值高斯白噪聲。

由多普勒頻移的測量原理可知,多普勒頻移與信號頻率成正比。徑向速度1 mm/s時不同信號頻率的多普勒頻移見表1[8]。太陽輻射中可見光的頻率為3.842×1014～7.878×1014Hz,可直接作為分光計的入射光譜,徑向速度測量精度可達1 cm/s。

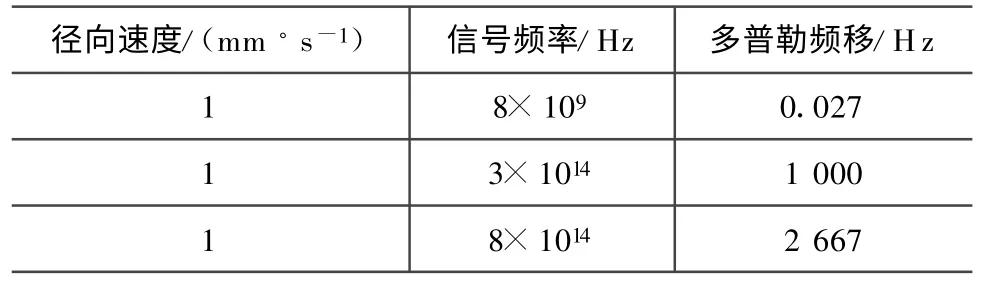
表1 多普勒頻移Tab.1 Doppler shift

3 基于信息融合的導航濾波算法

自主導航系統的狀態方程見式(2),其狀態模型誤差的協方差陣E[w(k)(w(k))T]=Q;系統的觀測方程分別為式(4)、(6);觀測噪聲的協方差陣分別為E[v1(k)(v1)(k)T]=R1,E[v2(k)v2((k))T]=R2。

3.1 信息分配

信息分配是在主濾波器和各子濾波器間分配系統的信息。系統噪聲Q和狀態方差Pg按信息分配原則

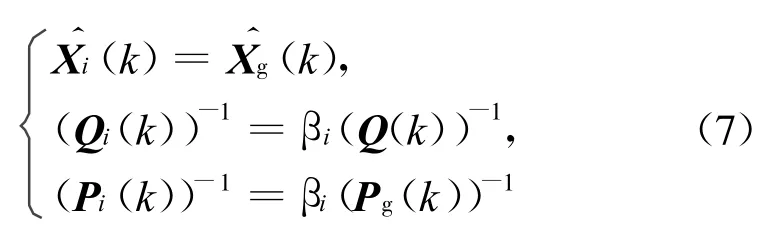
信息分配因子選擇的基本原則是在滿足信息守恒原理的前提下與局部濾波器的濾波精度成正比。根據局部濾波器的估計精度動態確定信息分配因子,能更好地反映子系統估計精度的變化,減小子系統失效或精度下降的影響。由矩陣理論可知：卡爾曼濾波中估計誤差協方差陣P的奇異值包含了系統各狀態估計的自協方差信息,以及各狀態估計的互協方差信息,反應了局部濾波器的濾波性能[10]。因此,本文用P的奇異值動態確定信息分配因子。令

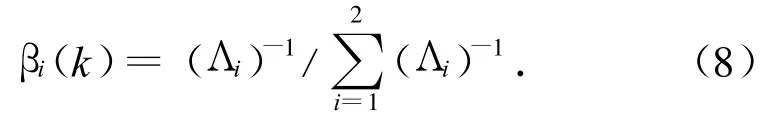
3.2 各子濾波器的狀態與測量更新

各子濾波器的狀態和測量更新方程為

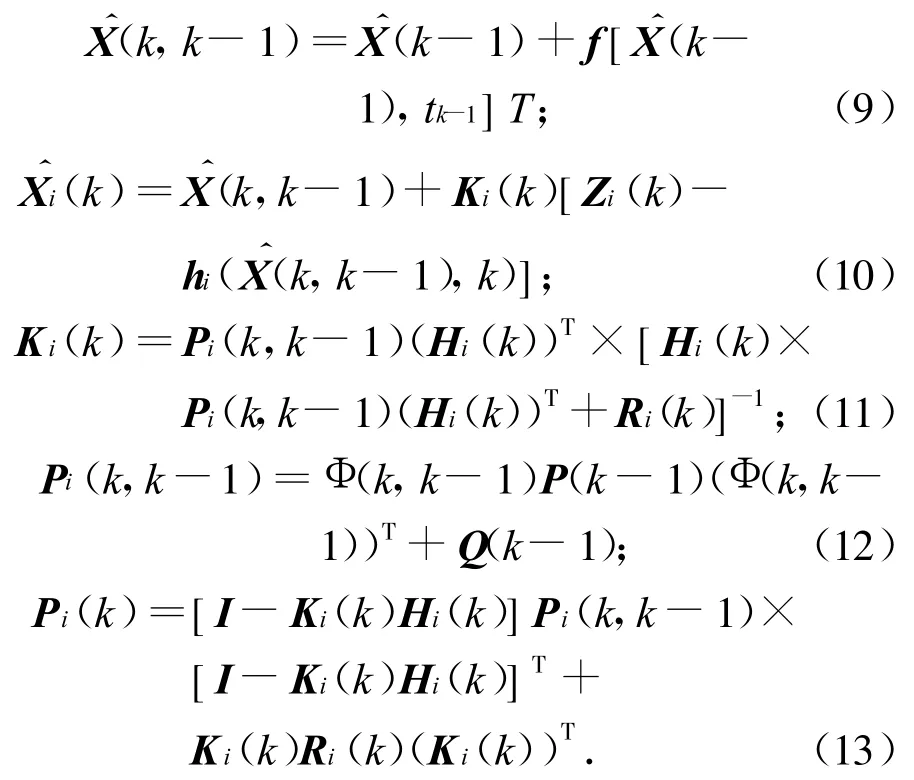
3.3 信息融合

經并行運算的各子濾波器的處理可得2個局部最優估值Xi(k),在主濾波器中按

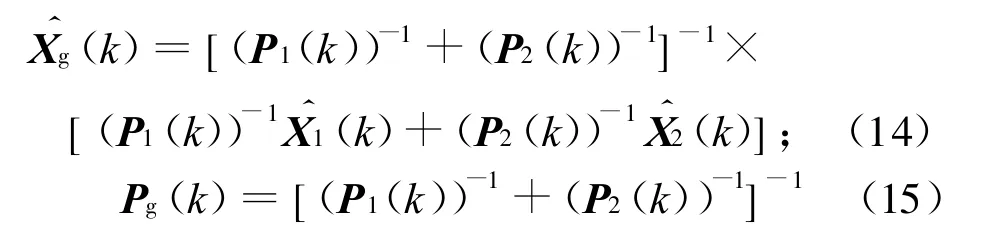
融合,得全局最優估值。

4 仿真

4.1 條件

以深度撞擊任務的實際飛行數據驗證本文的基于信息的深空巡航段自主導航算法。深度撞擊任務的行星際飛行時間從2005年1月18日至7月2日,初始與最終時刻探測器的位置和速度見表2[11]。深度撞擊任務中地球、Tempel/9P彗星和Deep Impact-1探測器的飛行軌跡如圖2所示。

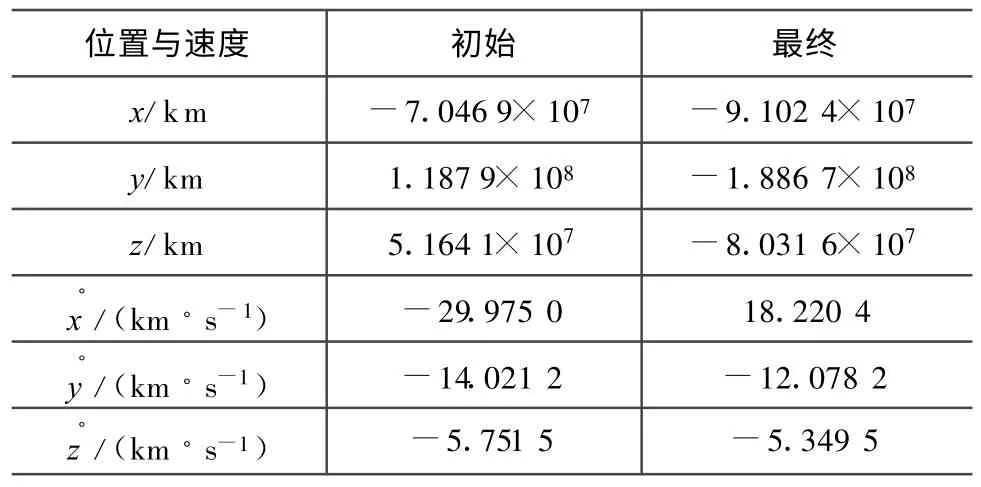
表2 探測器始末時刻的位置和速度Tab.2 Position and velocity at initial time

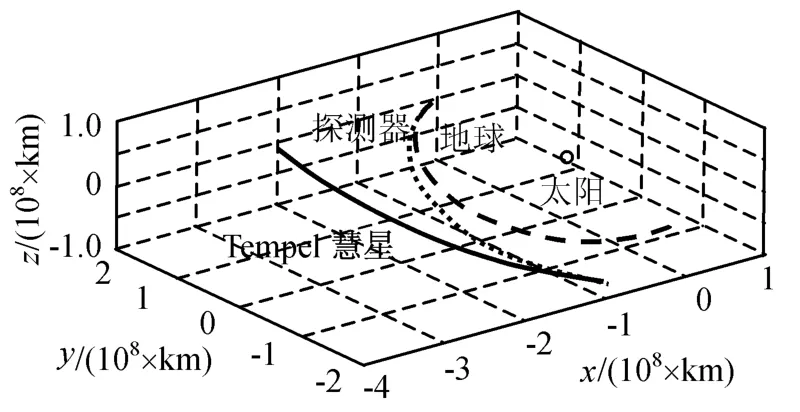
圖2 深度撞擊任務的飛行軌跡Fig.2 Trajectory of the Deep Impact mission

a)標稱軌道數據源于深度撞擊任務,初始位置誤差6×105km,速度誤差0.1 km/s;

b)取太陽視線矢量測量誤差5×10-5rad,探測器相對太陽的徑向速度測量誤差為1×10-5km/s;

c)考慮到探測器各任務系統間的規劃調度及各種測量信息的處理時間,取T=300 s,仿真時間Tf=2.1×106s。

4.2 結果與分析

用本文方法仿真所得探測器的位置和速度估計誤差分別如圖3、4所示,仿真結束時刻探測器的位置和速度估計誤差見表3。

由仿真結果可知：最終位置估計誤差小于95 km,速度估計誤差小于5×10-5km/s,表明本文的基于信息融合的深空巡航段自主導航算法的軌道參數估計結果滿足深空巡航段的精度要求。另仿真中發現姿態估計精度和敏感器的測量精度是影響導航系統軌道參數估計精度的主要因素。

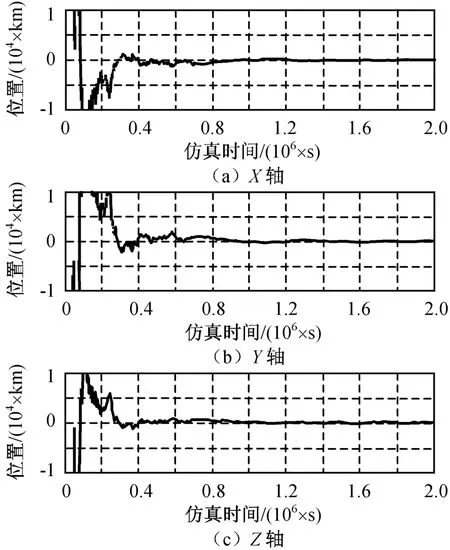
圖3 探測器位置估計誤差Fig.3 Position estimation error

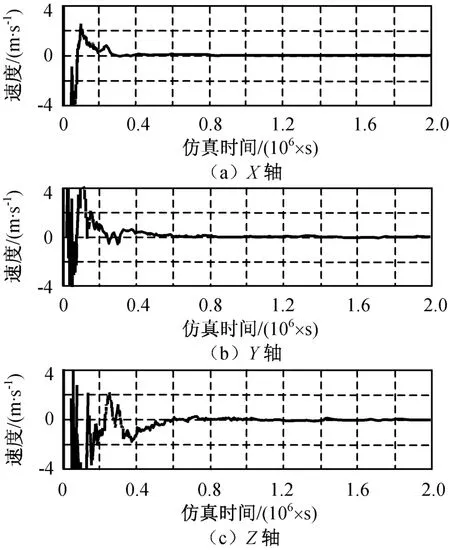
圖4 探測器速度估計誤差Fig.4 Velocity estimation error

5 結束語

為確定深空巡航段軌道,本文提出了一種基于信息融合的自主導航算法。基于太陽敏感器測得的太陽視線矢量和分光計測得的探測器相對太陽的徑向速度兩種不同類型的觀測信息,用信息融合技術和擴展卡爾曼濾波估計探測器的位置和速度。深度撞擊任務的實際飛行數據仿真結果驗證了該自主導航算法的可行性。

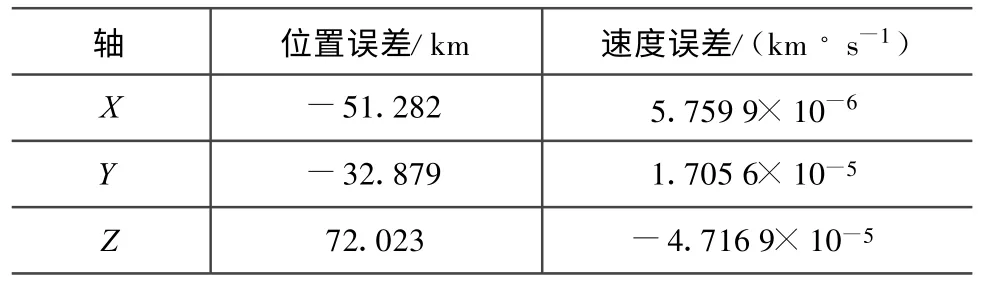
表3 探測器位置和速度估計誤差Tab.3 Position and velocity estimation error at f inal time

[1]DESAI S,HAN D,BHASKARAN S.et al.Autonomous optical navigation(AutoNav)technology validation report[R].Deep Space 1 Technology Validation Report-Autonomous Optical Navigation(AutoNav),JPL Publication 00-10,2000.

[2]MASTRODEMOS N,KUBITSCHEK D G,WERNER R A,et al.Autonomous navigation for the Deep Impact[C]//Proceedings of the AAS/AIAA Space Flight Mechanics Meeting.Tampa,Florida：AIAA,2006：1251-1271.

[3]MARINI A E,RACCA G D,FOING B H.SMART-1 technology preparation for future planetary missions[J].Advances in Space Research,2002,30(8)：1895-1900.

[4]KUBOTA T,HASHIMOTO T,KAWAGUCHI J,et al.Navigation,guidance and control of asteroid sample return spacecraf t：MUSES-C[C]//Proceedings 4thESA International Conference on Spacecraft Guidance,Navigation and Control Systems,ESTEC.Noordwijk,Netherlands：ESA,1999：ESA SP-425 2000,511-516.

[5]WU W R,TIAN Y L,HUANG X Y.Autonomous optical navigation for interplanetary exploration based on information of earth-moon[J].Journal of Harbin Institute of Technology(New Series),2003,10(3)：343-348.

[6]BHASKARAN S,DESAI D,DUMONT P J.et al.Orbit determination performance evaluation of the Deep Space 1,autonomous navigation system[C]//Proceedings of the AAS/AIAA Spaceflight Mechanics Meeting.Monterrey,CA：AAS,1998,98-193,1295-1314.

[7]徐文明,崔祜濤,崔平遠,等.深空自主光學導航小行星篩選與規劃方法研究[J].航空學報,2007,28(4)：891-896.

[8]GUO Y P.Self-contained autonomous navigation system for deep space missions[J].Advances in the Astronautical Sciences,1999,102(2)：1099-1113.

[9]章仁為.衛星軌道姿態動力學與控制[M].北京：北京航空航天大學出版社,1998.

[10]付夢印,鄧志紅,張繼偉.Kalman濾波理論及其在導航系統中的應用[M].北京：科學出版社,2003.

[11]BLUME W H.Deep impact mission design[J].Space Science Reviews,2005,117：23-42.