基于高階統計量的多模噪聲中的信號檢測

王 濤， 山 拜·達拉拜

（新疆大學 信息科學與工程學院，新疆 烏魯木齊 830046）

0 引言

非高斯噪聲的研究已經成為現代信號處理的核心問題之一，國內外做了很多的研究[1-7]。按照概率密度函數形狀，結合文獻[3-4]的方法，首次提出了多模噪聲的四種主要的簡化數學模型。多模噪聲總體上屬于非高斯噪聲，但兼容了高斯噪聲。因此，這里的方法有一定普遍意義。

高階統計量[6-8]尤其是高階譜的理論研究已經比較完善，近年來廣泛應用在信號檢測，參數估計等問題中。采用高階譜中的雙譜技術，以多模噪聲的第三種模型為噪聲背景，結合無慣性非線性變換器[9]，提出了基于雙譜的檢測方法，并給出了改進的自適應幅頻干擾抑制器[9]的物理模型。最后針對具體信號做了大量仿真驗證了其可行性，并與傳統的似然比檢測進行了簡單比較證實了其優越性。

1 多模噪聲的數學模型

隨著無線電技術的迅速發展，在復雜的電子設備中會出現無法預料的干擾和噪聲，破壞系統的功能。這些噪聲很多是非高斯噪聲，按照概率密度函數形狀對其進行研究，提出了多模噪聲。多模噪聲主要有四種簡化模型：

①高斯噪聲g(t)疊加振蕩過程，概率密度為：

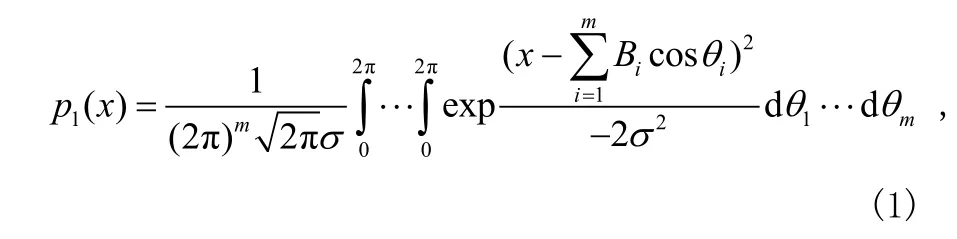
其中，σ2是高斯分量的方差；

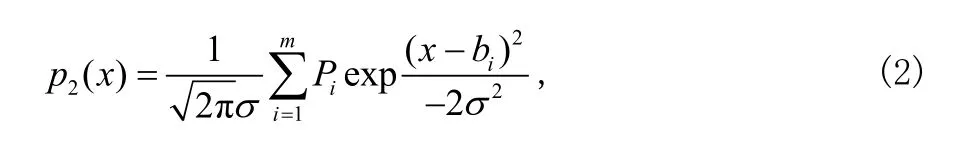
其中，為碼元的干擾概率。Pi的分布主要有兩

③當與滿足一定條件時，式（2）可寫成如下形式：

④混合模式，概率密度為：

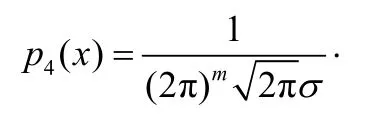
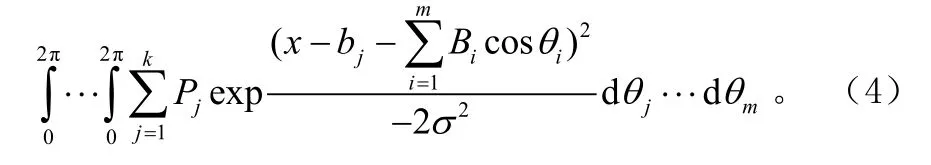
多模噪聲一般是多峰噪聲，也可能是單峰噪聲，這四種模型可以相互轉換，其最佳或準最佳的處理方法一般是化成第三種模型。

2 高階統計量

高階統計量是高階累積量和高階譜的統稱，高階統計量方法主要指高階累積量和高階累積量譜（高階譜）方法。高階譜中的雙譜，階數最低，處理方法簡單，含有功率譜中所沒有的相位信息，又能有效的抑制高斯噪聲，所以這里主要采用雙譜模型對信號檢測進行研究。

雙譜算法分為參數化和非參數化兩大類，下面給出一種改進的非參數化算法：

①將有限長數據{x(1),x(2),…,x(N)}分成 K段，每段 M個樣本，即 N=KM，并減去每段的樣本均值。必要時，可以每段補零得到快速Fourier變換的一個習慣長度M；

②計算每段的離散Fourier變換系數：

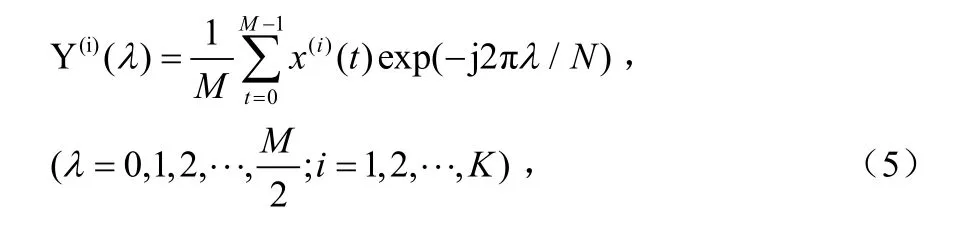
其中x(i)(t)(t =0,1,???,M-1)為第i段的數據；

③計算

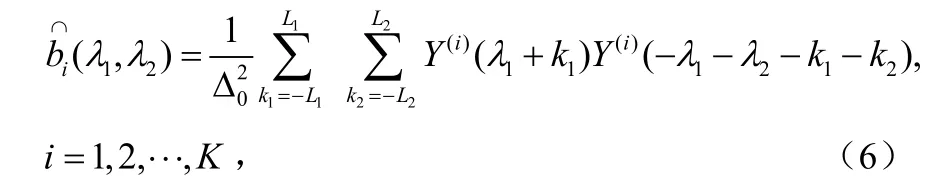
其 中 0≤λ2≤ λ1， λ1+λ2≤fs2，fs是 抽 樣 頻 率 ，Δ0=fsN0是頻率樣本空間， N0和 L1滿足M = (2 L1+1)N0；

④通過K段平均值得出雙譜估計值，有

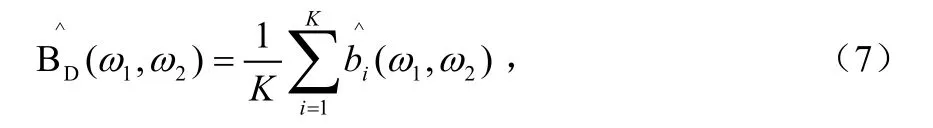
⑤提取雙譜的三個特征作為判斷的依據，定義其特征函數為 ()FE·。

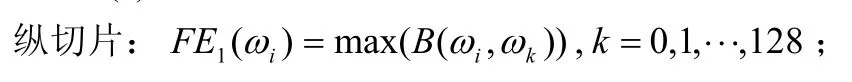
對角切片：

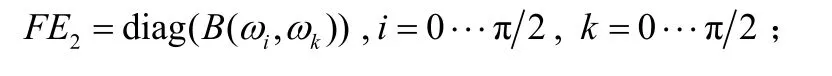
跡：

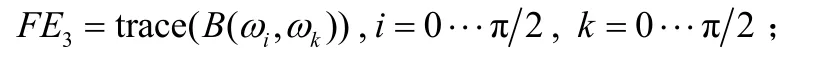
⑥以雙譜的跡作為軟門限，檢測雙譜的縱切片和對角切片在門限上峰的個數和位置，判定信號的存在。

算法的目的是在噪聲甚至強噪聲背景下，實時地處理采集到的數據，檢測出信號。

3 基于雙譜算法的多模噪聲中的信號檢測

在隨機信號處理的許多應用場合，如干擾信道中信號處理和最佳接收等，一個重要的課題就是信號檢測。對于傳統的信號檢測，最常用的方法是似然比檢測，但其存在兩個明顯缺點：①檢測對象必須滿足高斯假設，然后根據某種最佳準則劃分觀測空間進行判決；②當觀測信號 SNR下降時，系統檢測性能急劇下降，很難得到較高的檢測概率。對于加性多模噪聲，一種經典的理論方法是采用無慣性非線性變換器，但是需要噪聲和信號的一些先驗概率，或者假設噪聲參數已知。圖 1即為無慣性非線性變換器的結構。

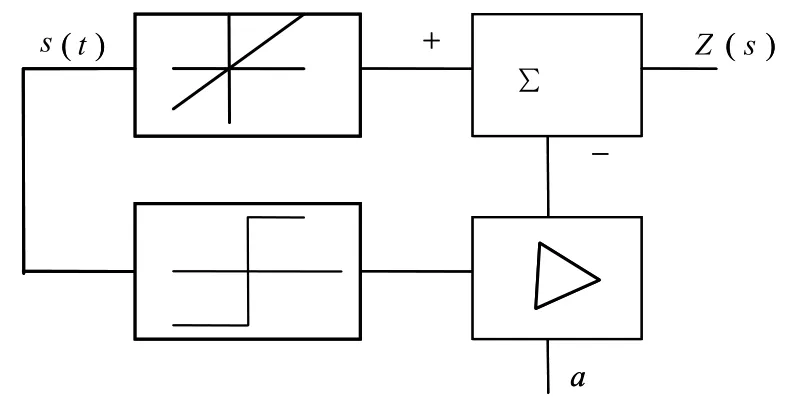
圖1 無慣性非線性變換器

無論各確定信號能量是否相等，該方法均適，可比較準確的的檢測信號。但同樣在觀測信號的 SNR很低時，會一定程度上造成檢測概率的下降。結合雙譜技術，用雙譜檢測器代替傳統的門限判決器，改進基于無慣性非線性變換器的自適應幅頻干擾抑制器，結構圖如圖2所示。

假設變換器的輸入端信號為，則無慣性非線性變換器的特性可表示為：

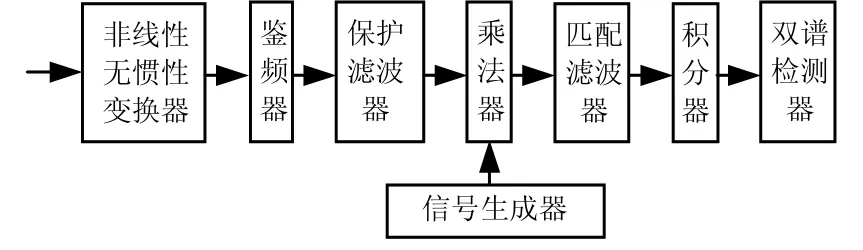
圖2 改進的自適應幅頻干擾抑制器

采用雙譜技術檢測多模噪聲背景下的信號，只要信號雙譜信息足夠大，即使 SNR很小，依然可獲得較高的檢測概率。研究多模噪聲的第三個模型，假設信號為一正弦信號，取 128個采樣點，通過雙譜算法得到估計，取 SNR=-10 dB。仿真結果如圖3、圖4和圖5所示。

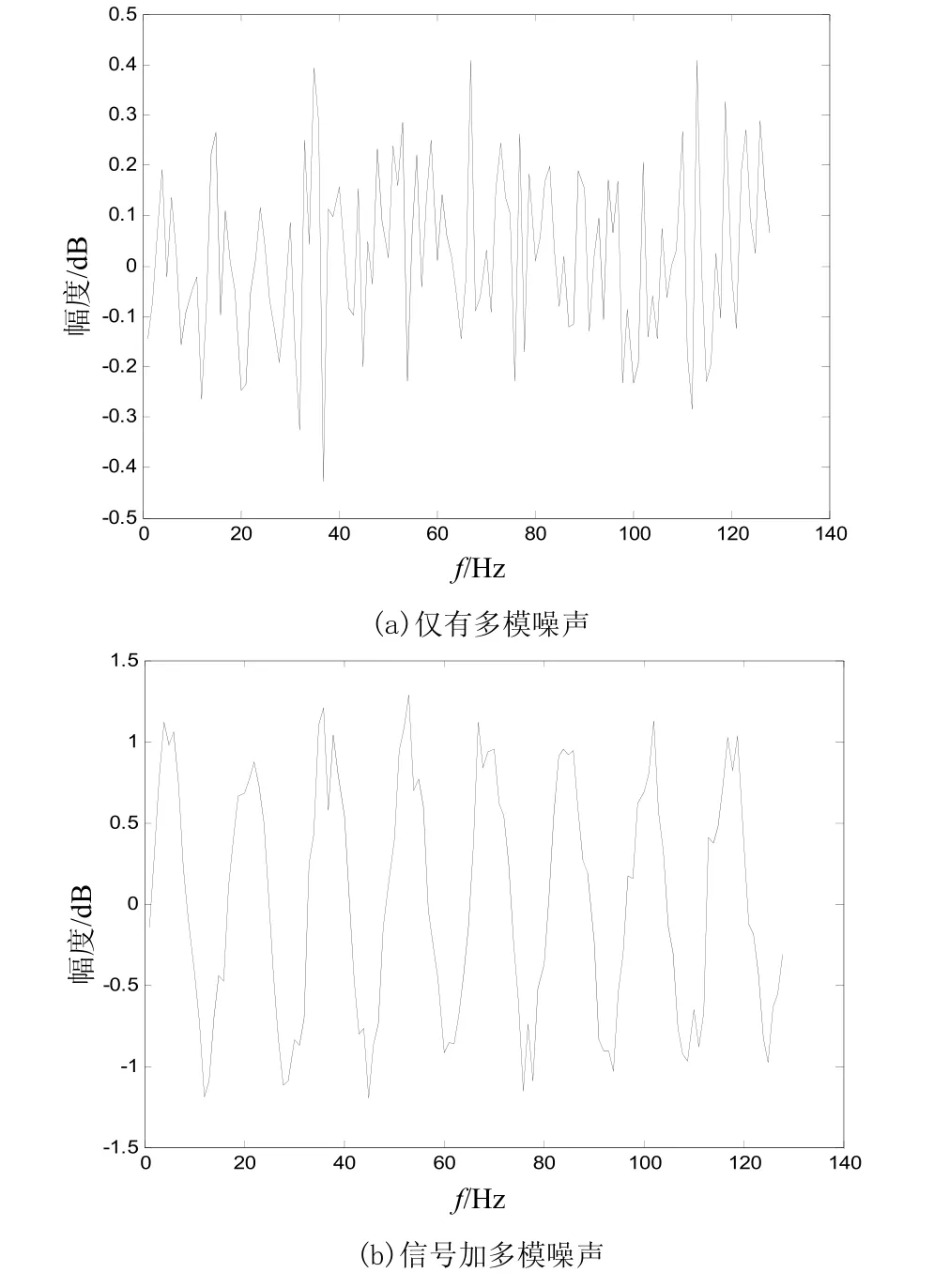
圖3 觀測信號波形

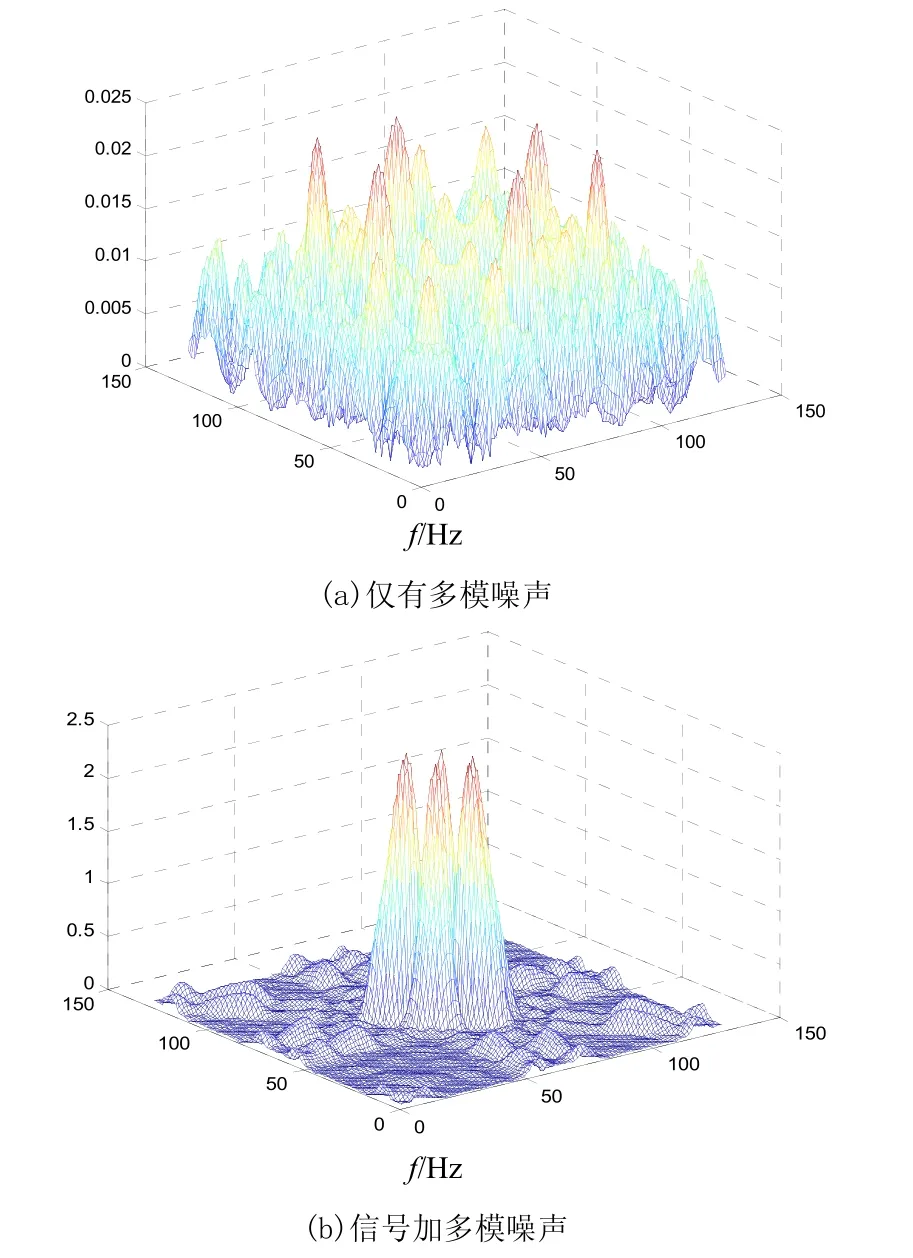
圖4 觀測信號雙譜立體

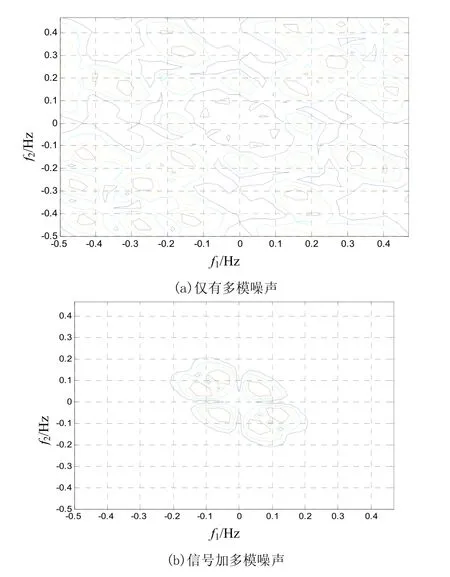
圖5 觀測信號雙譜平面

對比可知：在時間域接受SNR較低，而在雙譜域接受SNR較高，經過該處理信號的SNR大大提高，更有利于信號檢測，可以明顯的判斷出是否存在信號。

在多模噪聲干擾下，雙譜檢測與傳統的似然檢測的檢測概率比較。很容易看出，雙譜的檢測性能要高于似然比檢測，如圖6所示。

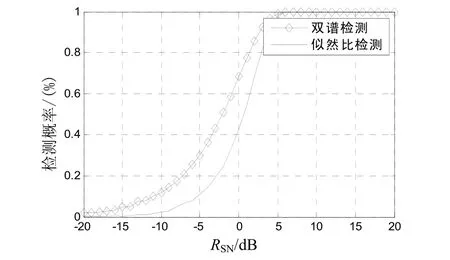
圖6 多模噪聲下檢測概率比較

在實際當中，噪聲往往是雙模或者多模的，傳統的檢測方法需要對噪聲有很多的先驗知識，才能夠比較準確的檢測信號。但當在強噪聲背景或 SNR很低的情況下，往往無法得到滿意的效果。高階譜尤其是雙譜可以在信號檢測中抑制分布未知的高斯噪聲，結合經典的無慣性非線性變換器，會成為多模噪聲檢測的最佳或準最佳檢測方法。

4 結語

在復雜的環境中，如軍事、民航等，干擾噪聲多為非高斯噪聲，本文根據概率密度函數形狀提出了多模噪聲的數學模型。運用高階統計量法，尤其是雙譜技術在多模噪聲背景下對信號檢測進行了研究。理論和實驗仿真表明，雙譜可以抑制高斯噪聲的影響，同時可以在復雜的背景下以較高的檢測概率檢測信號，優于傳統的信號檢測方法。但在實際的隨機信號處理中，高階統計量往往無法得到嚴格意義上的真實值，雙譜不能嚴格的完全濾除高斯噪聲。所以在復雜噪聲背景下，如多模噪聲，結合無慣性非線性變換器，改進了自適應幅頻干擾抑制器，給出了檢測的物理模型，可精確檢測或估計信號。只是某些無慣性非線性變換器比較復雜，可用軟件處理接收信號，更加方便。

[1] HINICH M J, WILSON G R.Detecion of Non-Gaussian Signals in Non-Gaussian Noise Using the Bispectrum[J].IEEE Transaction on Acoustics,Speech and Signal Processing,1990,38(07)：1126-1130.

[2] KOLODZIEJSKIK R D, BET J W,CORP M,et al. Detection of the Weak Random Signals in IID non-Gaussian Noise[J]. IEEE Transactions on Communication,2000,48(02)：222-230.

[3] 山拜·達拉拜，黃玉劃.幾類非高斯噪聲模型的轉換研究[J].電子學報，2004，32（07）：1090-1093.

[4] 黃玉劃,山拜·達拉拜.多模噪聲理論及其在通信保密中的應用[J].電訊技術,2008(02)：20-24.

[5] 盧廣芝.非高斯噪聲中信號的神經網絡檢測[J].通信技術,1997(04),55-58.

[6] 邱天爽.統計信號處理[M].北京：電子工業出版社,2004.

[7] 張賢達.時間序列分析——高階統計量法[M].北京：清華大學出版社,1996.

[8] ROSA J J G, PIOTRKOWSKI R, RUZZANTE J E.Higher Oder Statistics and Independent Component Analysis for Spectral Characterization of Acoustic Emission Signals in Steel Pipes[J].IEEE Transacions on Instrumentation and measurement,2007,56(06)：2312-2321.

[9] 山 拜 ·達 拉 拜 .Методы Защиты от Помех в Каналах Радиосвязи[J].Известия Белорусской Инженерной Академии,1997,1(03)： 67-72.