基于廣義形態濾波的圖像去噪方法研究

吳時蘭， 錢盛友

（湖南師范大學 物理與信息科學學院，湖南 長沙 410081）

0 引言

圖像退化的最重要原因就是噪聲的加入，因此去噪處理是進行圖像分析和識別前的必要步驟。針對不同類型的噪聲有不同的去噪方法。通常用均值濾波去除高斯噪聲,而脈沖噪聲能被中值濾波較好的濾除[1]，但存在細節信息丟失現象,并且在噪聲強度大時不能達到很好的去噪效果。近年來由于形態學算子在二值圖像處理方面廣泛而成功的應用,灰度形態學逐漸成為圖像處理領域的一個重要工具。利用形態學開閉或閉開交替濾波器能去除多種類型的圖像噪聲，但傳統的形態學開閉和閉開運算對強噪聲污染的圖像去噪效果卻不理想。現基于形態學理論,對形態學算子進行了改進,并將其用于椒鹽噪聲的濾除,分析了其去噪效果。

1 灰度圖像的形態學處理

1.1 經典灰度形態學的基本理論

在灰度形態學中，最基本的兩種運算是膨脹和腐蝕運算,其他形態學變換都是這兩種運算根據一定的順序進行組合的復合運算。

令f (x,y)為灰度圖像, b (x,y)是結構元素, Df和Db分別為函數f和b的定義域，采用在定義域中取零的扁平結構元素，則相應的膨脹和腐蝕算子可表示為[2]：

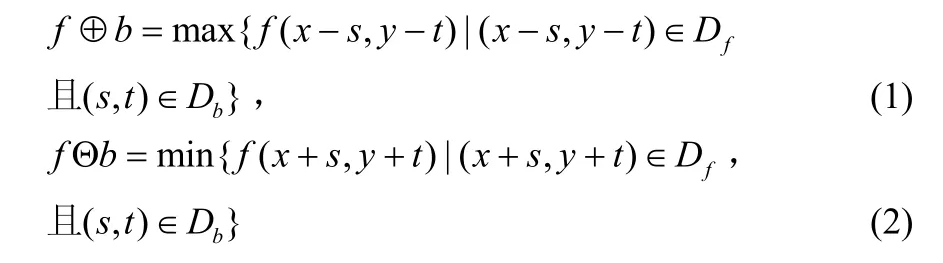
在灰度形態學處理中還有兩種非常重要的運算方法：形態開運算和形態閉運算[3]。

開、閉運算分別定義為：

1.2 廣義形態學

Maragos利用相同的結構元素，定義了形態開閉和形態閉開濾波器[4]。對于形態開閉濾波而言，首先進行的開運算在去除正脈沖噪聲時，同時增強了負脈沖噪聲，若再采用相同的結構元素進閉運算，就不能有效地去除全部的負脈沖噪聲。同樣，采用相同結構元素的形態閉開濾波器也不能有效地去除全部的正脈沖噪聲。文獻[5]提出了廣義的開閉、閉開形態濾波。

廣義的形態開閉濾波和閉開濾波的定義為：

b1，b2為兩個結構元素，且 b1?b2。

廣義的開閉和閉開運算能較好的去處脈沖噪聲[5]。對當圖像被強噪聲污染時，這種方法卻得不到很好的去噪效果。

1.3 改進的廣義形態學

開運算是先腐蝕后膨脹。當圖像被鹽噪聲污染時，利用腐蝕運算，鹽噪聲可以被圖像的灰度值代替，即鹽噪聲被有效地濾除；當圖像被椒噪聲污染時，利用膨脹運算，椒噪聲可以被圖像的灰度值代替，即椒噪聲被有效地濾除。當噪聲強度大時，在一個小小的鄰域中有可能都是被噪聲污染的圖像信息。當運用腐蝕運算時，鹽噪聲極有可能被椒噪聲代替，出現更糟的情況是圖像信息被椒噪聲代替；而當運用膨脹運算時，椒噪聲極有可能被鹽噪聲代替，甚至出現圖像信息被鹽噪聲代替的糟糕情況。因此，噪聲強度大時，運用開閉、閉開運算不能有效地去除噪聲，甚至有可能使圖像變得更糟糕。

1.3.1 改進的腐蝕運算和膨脹運算

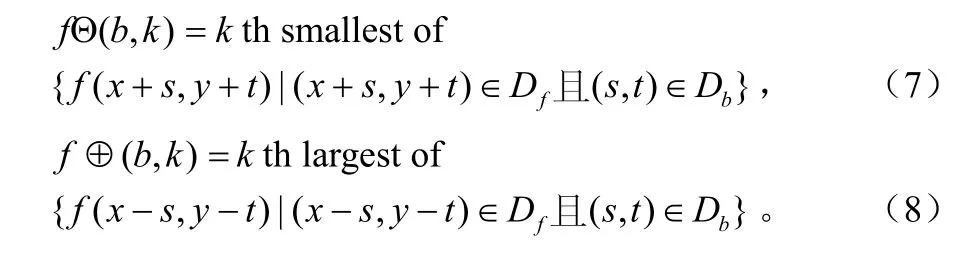
改進的腐蝕運算不是用像素鄰域的最小灰度值代替該像素的灰度值，而是用該像素鄰域的第k個小值取代該像素的灰度值。當圖像被高密度的鹽噪聲污染時，運用改進的腐蝕運算，鹽噪聲極有可能被圖像信息取代，即有效地去除了亮噪聲。同理，改進的膨脹運算能有效地去除椒噪聲。

1.3.2 改進的廣義開、閉運算

改進的廣義開運算定義為：

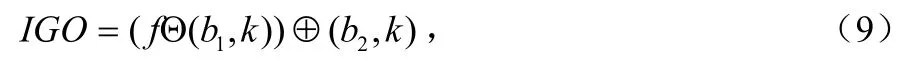
改進的廣義閉運算定義為：

1.3.3 改進的廣義形態學濾波

中值濾波、形態濾波對圖像的每一個像素都要進行處理，這樣有可能使不含噪聲的圖像的灰度值被相鄰點的灰度值代替，使圖像變得模糊，且去噪時間較長。

這里先確定被污染圖像中的各個像素是否被噪聲污染，依據像素是否是該鄰域（其中鄰域采用 3×3的方形窗口）的最大值或最小值來確定該像素是否被噪聲污染。如果是的話，就認為該點被噪聲污染，再對被污染點采用改進的廣義形態學濾波；如果不是的話，就認為這點沒有被噪聲污染，不對它進行處理。

2 仿真實驗及結果分析

在實驗中使用205 px×232 px的“tire.tif”的圖像，分別加入噪聲強度為 0.1～0.8的椒鹽噪聲。通過仿真發現，當噪聲強度為0.5時，k取4時去噪效果最佳。這里的濾波方法與廣義形態濾波、3×3中值濾波、5×5中值濾波進行了比較，結果如圖1所示。從圖1可以看出：在圖像噪聲強度大時，廣義形態濾波和3×3中值濾波的去噪效果非常差，5×5中值濾波不能完全去除噪聲，而提出的方法濾波效果較好。為了判定這幾種方法的好壞，可以用評價圖像質量的客觀標準峰值信噪比（PSNR）、均方誤差（MSE）來衡量各種方法的去噪效果。其結果如表1所示。

圖1 噪聲強度為0.5時不同方法的濾波效果

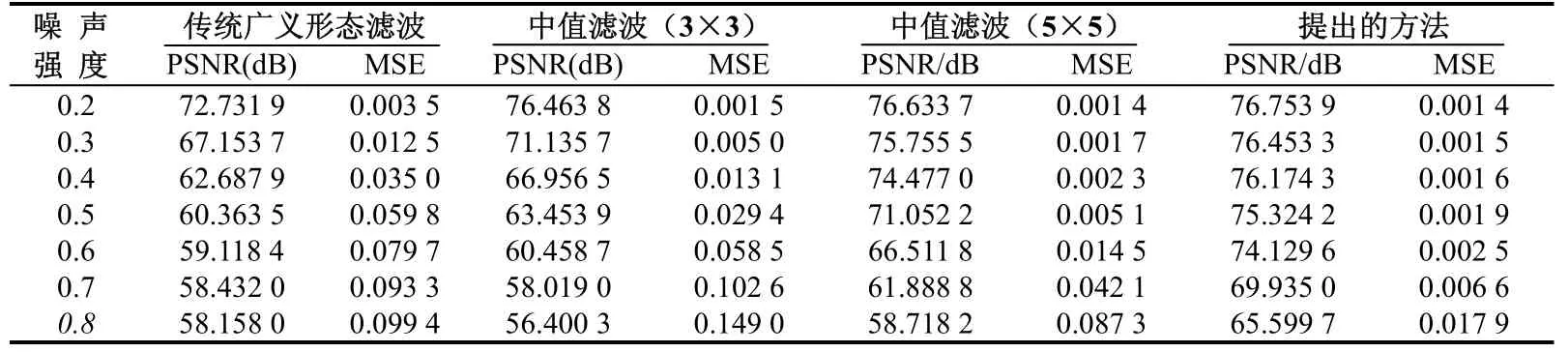
表1 去噪圖像的峰值信噪比和均方誤差

從表 1中可以看出，這里的方法的去噪效果優于其它 3種方法，當噪聲強度愈大時，這里的方法的優勢愈明顯。

3 結語

針對傳統的形態濾波方法在噪聲強度大時去噪效果差的缺陷，提出了一種改進的廣義形態濾波方法。首先依據像素是否是該鄰域的極值來確定該像素是否被噪聲污染，然后對被噪聲污染的像素進行改進的廣義形態濾波。因為不需要對每個像素進行處理，所以濾波時間被縮短。用該方法對含不同強度椒鹽噪聲的圖像進行了處理，并與其它方法進行了比較。仿真結果表明，在強噪聲情況下，提出的方法在視覺效果和圖像質量客觀評價指標上均優于傳統形態學濾波和中值濾波。相對原始無噪圖像，去噪后的圖像有些模糊。怎樣在既能濾除噪聲的同時又能有效地保持細節，是下一步研究的方向。

[1] 董漢磊，徐利平，高穎敏，等.基于Bior小波變換和中值濾波的圖像去噪[J].通信技術，2009, 42(11)：171-175.

[2] 楊征宇,夏慶觀.形態學算法的去噪處理在自由曲面重構中的應用[J].模具工業，2009,35(09)：22-25.

[3] 喬德江，陳鴻昶.基于數學形態學的模糊子筆畫提取[J].通信技術,2009,42(02)：174-178.

[4] 崔屹.圖像處理與分析數學形態學方法及應用[M].北京：科學出版社,2000：98-135.

[5] 白銀剛,于盛林,李建明.一類新的廣義開和廣義形態閉濾波器[J].中國圖像圖形學報，2009,14(08)：1523-1529.