UWB CHIRP信號的多徑時延頻域提取方法

陸 侃， 卓永寧

(電子科技大學 通信抗干擾技術國家級重點實驗室，四川 成都 611731)

0 引言

超寬帶（UWB）是近年來興起并快速發展的一項無線通信技術，是當前的熱點研究技術之一。線性調頻脈沖因其高處理增益、低功耗、抗多徑干擾、抗多普勒頻移等優點，已得到廣泛研究。近年來，Chirp信號被廣泛地應用于信道估計中，而多徑時延的估計有著很重要的作用。其中Chirp信號自相關解調的方法比較常用，但相關后 sinc函數旁瓣對多徑提取影響比較大，分辨率也不高[1]。隨后的一些高階累積量算法有計算量太大的缺點，不適合實際應用。

在對這些優缺點做分析研究的基礎上，提出了對Chirp信號做調制后用FFT運算提取頻差這一快速有效的算法[2]，在頻域獲取信息以求得多徑時延。此算法不但具有與相關解調算法相同的分辨率，且其尖銳的波形特征使讀取信息更加精確，且方法簡單，計算量不大，適合在移動定位系統中使用，獲取所需要的信道參數等。

1 算法簡介

假設信號發射點位于x0處，信道中有一個多徑x1，位于與x0相距R1m的地方。信號由x0發出經x1反射后經過時延t1（t1= R1/2c）被發射點處的接收機接收。

發射信號是：

B為Chirp信號帶寬，Tc為脈寬,Ω載波頻率。因此發射點接收到的返回信號可寫為：

Γ為系數常量。該反射信號由修正過的相關接收機進行處理，它包含了exp(jΩt)項來去載頻，且包含發射的chirp信號的副本，輸出y(t);

與t1平方項有關的相位項是一個復常量，其他復指數項均為t的線性函數，因此代表恒定頻率的復正弦。對接受信號做FFT變換后[3]，即可得到頻率

f1與t1成正比，從而f也與x1相對于x0的距離R1成正比。由混頻、經FFT處理后檢得的頻率可以算出距離差

如果有多個多徑反射點,則信號被處理后的輸出只是多幾個如式（5）的疊加：

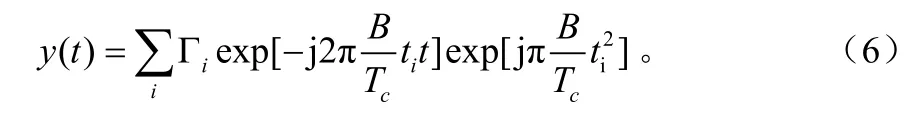
即對于每個多徑反射點，經混頻、FFT處理后頻域信號中包含一個不同的頻率差fi=-Bti/Tc，對y(t)進行頻譜分析可以獲得多徑時延：

2 仿真驗證

2.1 UWB信道

UWB信號可表示為一個聯合連續Nakagami m，離散泊松隨機變量到達時間超指數分布的離散隨機變量，其關鍵參數包括簇到達率，束到達率（混合泊松模型參數），簇衰減因子，簇時延固定參數，Nakagami m因子均值，Nakagami m因子方差，可選的功率時延剖面（PDP）形狀[4]。

考慮文獻 IEEE 802.15.4a的 UWB信道模型，Saleh-Valenzuela（SV）模型的沖激響應一般表示為：

式（8）中，al,k為第l簇中第k條路徑的系數，Tl為第l簇的時延，tk,l是第l簇內第k徑相對與簇到達時間Tl的時延，tk,l為相位。

IEEE802.15.4a信道模型根據實測環境分為9組，這里考慮的是戶外視距傳播環境(num 9),信道脈沖見圖1。

圖1 Chirp IEEE802.15.4a信道（類型9）

2.2 Chirp信號相關解調

Chirp更為一般的解調方法是利用Chirp信號的自相關性[5]。Chirp信號的表達式為：

Tc為脈沖寬度，f0為信號起始頻率B=|u|Tc為信道帶寬。

Chirp信號具有良好的自相關特性。其自相關函數為Sinc函數形式：

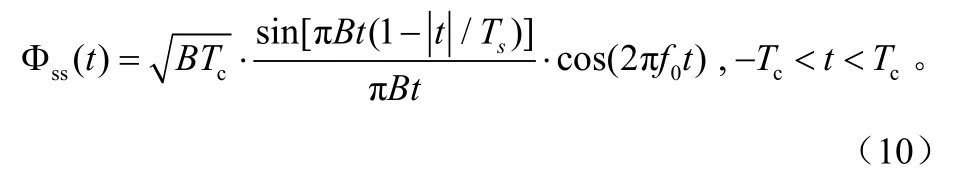
在 t=0時刻，Фss(t)的包絡取得最大幅度值當t=±1/B時，Фss(t)的包絡為0。圖2上下分別為Chirp信號的自相關與互相關函數。

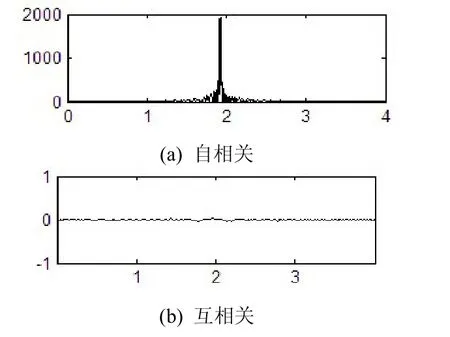
圖2 Chirp信道的自相關與互相關函數

這一特點被應用于Chirp-BOK調制系統，將UP-Chirp信號與 DOWN-Chirp信號互相作為其匹配濾波器的沖擊響應，進行相干匹配濾波。Chirp信號自相關函數尖銳的時域特性也可被用于多徑時延的估計，多徑引起的時延會導致相關解調后峰值的移動，被檢測到的多徑最小時延為 1/t B= 。圖3為上升頻Chirp信號過圖1所示的信道后被下降頻信號匹配濾波，高斯白噪聲信道的RSN=-15。雖然圖1中明確顯示信道中存在三個多徑信號，但在圖3的相關解調結果中，難以確定多徑信號的確切數量，同時也難以確定多徑信號之間的延時差，同時壓縮脈沖本身也有很大的旁瓣，降低了確定時延差的分辨率。

2.3 仿真驗證

基于算法簡介中的思想與實際情況，設置如圖4所示的系統仿真圖。

圖3 用Chirp信號自相關方法檢得的多徑脈沖

仿真中，設Chirp信號的帶寬是 5 MHz，采樣頻是200 MHz，載波頻率為5 MHz，信號的周期為10 us，一個周期采得樣點數2 000。圖5為Chirp信號經圖4系統處理后獲得的頻域信號，設置了與圖 3相同的RSN（-15），多徑很容易被辨認。

圖4 實驗系統

圖5 采用混頻后FFT的方法檢測的多徑脈沖

3 算法分析

根據公式（6），Δt的延時導致的頻移為

對信號s(t)用N個點采樣得sN(t)，對sN(t)做FFT，所得頻域 sN(k)的每兩根譜線間的距離 f0=fs/N=fs/(fSTC)=1/Tc(fs為信號的時域采樣頻率)，f0被稱為頻譜的分辨率。f0對應的時域時延為

所以用這里的方法可以檢測到的最小多徑時延為t0=1/B，相關解調的方法可檢測到的最小多徑時延為t=1/B，所以兩種方法在算法精度上是一致的。對 Chirp信號做自相關后得到的sinc函數，其旁瓣對多徑信號的正確獲取造成了很大影響（如圖4所示）。而這里把時域信號變換到頻域處理去處理，在獲得與相關運算相同算法精度的前提下，不僅避免了旁瓣的影響，且更直觀，更易精確讀取（如圖5所示）。

仿真中，信道的采樣頻率為200 MHz，信道一個脈沖時延ts0=1/fs為5 ns，對應的多徑距離Δt=(ts0c)/2=0.75 m（c為光速），導致的頻率變化Δf0=B/Tcts0，為2.5 kHz，Δf的頻率變化所對應的多徑距離為：

而由于仿真用FFT算法，受頻譜分辨率f0的影響，無法測得Δf0。f0=fs/N= fs/(fSTC)=1/Tc，所以適當得延長Tc，可以減小f0，使分辨率提高；也可以采用更精確的現代譜估計算法，如ARMA，MUSIC等[6]，使提出的算法的多徑分辨率更大。

4 結語

提出了一種在采用超寬帶Chirp信號的移動定位系統中進行信道時延估計和多徑分辨的新方法，即先對信號做混頻再用FFT求取頻率，并對這個算法的性能做了研究與分析。該方法把時域信號轉換到頻域做分析，很好地避免了時域相關后旁瓣帶來的影響，算法不但具有與相關解調算法相同的分辨率，且其尖銳的波形特征使讀取信息更加精確，且方法簡單，計算量不大，適合在GSM、CDMA等移動通信系統中使用。

[1] 王曉偉，李昕，費敏銳. Chirp擴頻通信系統扛噪聲性能研究[J].通信技術,2009,42(03)：15-17.

[2] RICHARDS M A. 雷達信號處理基礎[M]. 北京：電子工業出版社,2008：139-153.

[3] 胡廣書. 數字信號處理理論、算法與實現[M]. 第2版.北京：清華大學出版社,2003：93-168.

[4] IEEE.IEEE 802.15.4a-2005,Channel Model-final Report[S]. USA：IEEE, 2005.

[5] XIA X G. System Identification Using Chirp Signals and Time-variant Filters in the Joint Time-frequency Domain[J].IEEE Transactions on Signal Processing, 1997,45(08)：2072-2084.

[6] BASU A J, PALIWAL K K A.A Comparative Performance Evalution of Adaptive ARMA Spectral Eatimation Methods for Noisy Speech[J]. IEEE Digital Object Identifier,1988（01）：691-694.