高速數字通信中的遠端串擾建模分析

劉 鵬， 鞠華方， 劉艷霞

（浪潮高效能服務器和存儲技術國家重點實驗室，山東 濟南 250101）

0 引言

如今的高速數字通信系統正在加速進入10 Gb/s以上的高速信號時代。通信系統中信號速率的提升，走線密度的增大及通信空間的不斷減小導致信號完整性問題越來越明顯。遠端串擾就是高速數字通信中由互容與互感效應引起的一種信號完整性問題[1-3]。

在低速時代，不受重視的遠端串擾問題對于高速信號就完全不是一回事了。高速芯片非常低的電壓門限值加上非常大的d/di t和d/dv t的變化率，互容與互感即使比較小也會引起終端 IO口的誤觸發，導致信息傳輸失敗，引起信號完整性問題[2]。

通過分析高速數字通信傳輸鏈路中動態侵害信號線與靜態被侵害信號線之間的作用，針對電場與磁場的串擾分別建立等效互容與互感電路模型[1,3]，并通過分析動態信號線與靜態信號線之間的互容與互感作用推導出數學表達式，得到最終影響遠端接收端信號質量的遠端串擾電壓計算公式[3-5]。根據推導出的公式現提出減小遠端噪音的改進策略，并通過HSPICE仿真數據驗證電路模型與數學公式的準確性。

1 等效電路建模

為了分析兩根信號線之間的串擾關系，首先建立單根信號線的等效電路模型[1,3]，如圖1所示。

圖1 單根信號線的等效電路模型

R為單位長度信號線的串聯電阻；

L為單位長度信號線的串聯電感；

G為單位長度信號線與返回路徑之間的并聯電導；

C為單位長度信號線與返回路徑之間的并聯電容。

在此RLGC模型中，C和L會隨著信號電壓與電流的變化產生變化的電場與磁場，進而通過電場與磁場影響周圍的信號線，這就會產生串擾噪音。為了更加直觀的描述這種電場與磁場，采用互容與互感來描述產生串擾噪音的電場與磁場作用，如圖2所示。

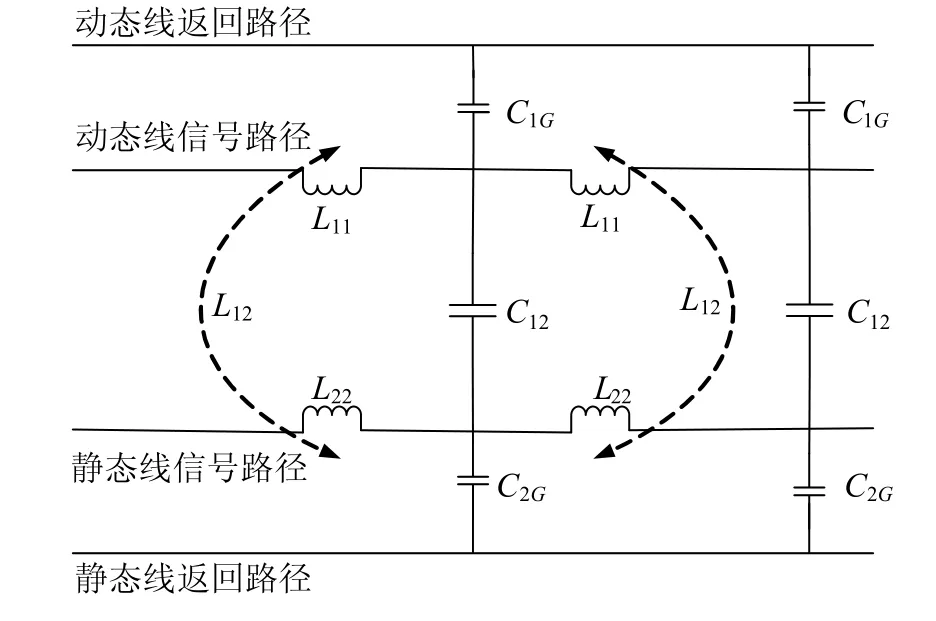
圖2 兩根信號線的串擾等效模型

圖為兩根信號線之間的串擾等效電路模型，這里忽略R和G的作用，因為這兩個參數與串擾無關[1]。為了便于計算與理解，此處假設兩根信號線所有性質一致，長度為 Len，終端完全阻抗匹配，且完全平行。其中：

C1G為單位長度動態信號線與返回路徑之間的自身并聯電容；

L11為單位長度動態信號線的自身串聯電感；

C2G為單位長度靜態信號線與返回路徑之間的自身并聯電容；

L22為單位長度靜態信號線的自身串聯電感；

C12為單位長度動態信號線與靜態信號線之間的互容；

L12為單位長度動態信號線與靜態信號線之間的互感。

這里，為了表達方便設定， C11= C1G+ C12、C22= C2G+ C12。由于假定動態線和靜態線性質完全一致，所以有 C11= C22、L11= L22。

在靜態線產生噪音的唯一途徑就是動態線上有變化的電壓與電流造成的電場與磁場。

2 容性耦合噪音

為了分析簡便，將互容與互感造成的影響分開來考慮，首先計算互容引起的遠端耦合噪音電壓，如圖3所示。

由于信號只在上升沿存在變化的電壓，所以先考慮上升沿瞬間通過互容12C 耦合到靜態線上的電流噪音12CI 。

其中：

Tr為動態線上信號的上升沿時間；

v是信號傳播速度；

Δl為 Tr時間內信號在動態線上的延伸長度；

C是Δl長度上的耦合電容；

V1是動態線上的電壓變化。

圖3 互容串擾等效電路模型

噪聲電流在靜態線上前后方向上的阻抗一致，所以噪聲電流向前與向后的電流量相等，流向靜態線遠端的電流為：

把式（1）、式（2）和式（3）合并，得到式（4）：

由于 ICFront向遠端傳播的速度與動態線上信號上升沿向遠端傳播的速度相等，所以 ICFront會隨著動態線上信號做積分，積分的時間長度等于信號在動態線上傳播的時間長度Td，ICFront在 Td內積分得到電荷 QC。電荷 QC將會在信號到達遠端的上升沿時間 Tr里得到釋放， C2為 Tr時間內空間延伸長度上靜態線的電容[1-3]。

所以最終在靜態線終端得到的電壓如下：

3 感性耦合噪音

如圖4所示，同樣為了研究簡便，這里只研究互感引起的耦合噪音電壓。

由動態線上信號上升沿電流的變化引起的耦合到靜態線上的互感電壓12LV 為：

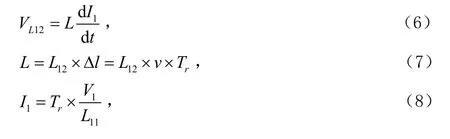
其中：

L是lΔ長度上的耦合電感；

I1是動態線上的電流的變化。

由式（6）、式（7）和式（8）式可得：

互感電壓在靜態線上引起的電流為：

圖4 互感串擾等效電路模型

與互容同樣的道理，互感引起的電流在前后方向上的阻抗一致，所以噪聲電流向前與向后的電流量相等，且前向互感電流LfrontI 在時延長度dT內積分得到的電荷LQ也會在rT時間內釋放[1,6]：

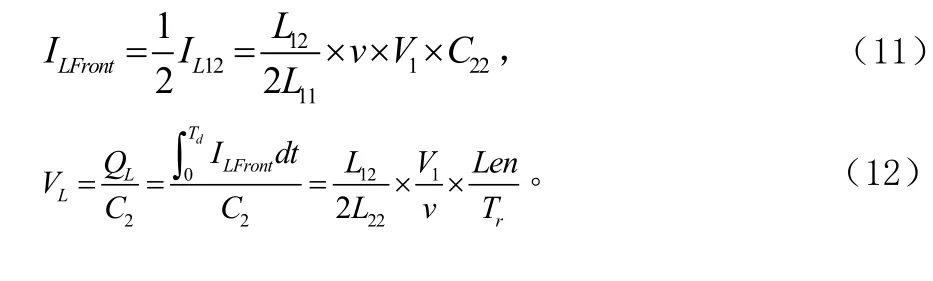
4 遠端串擾公式及改善措施、仿真驗證

由于互容與互感引起的串擾電流的方向相反，所以得到通信鏈路中遠端串擾噪音的計算公式為：

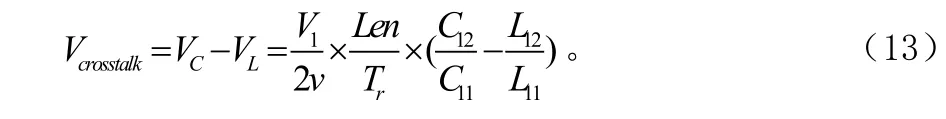
由式（13）就可以得到改善遠端串擾噪音的方法[1,4,5]：

①減小動態線的信號電壓1V；

②減小互感與互容耦合的長度Len；

③增大信號的傳播速度，也就是使用介電常數小的材質做PCB；

④增大信號的上升時間rT；

為了證明推導公式的準確性，可以使用 HSPICE仿真工具來驗證。設置動態線與靜態線完全平行且線寬線距均為 4 mil，線長20 inches，介電常數為4，微帶線，終端阻抗匹配。由HSPICE得到的RLGC model如下所示：

.MODEL Crosstalk W MODELTYPE=RLGC, N=2

+ Lo = 2.871471e-007

+ 5.941408e-008 2.871471e-007

+ Co = 1.049110e-010

+ -9.3579621e-012 1.049110e-010

+ Ro = 3.737469e+000

+ 0.000000e+000 3.737469e+000

+ Go = 0.000000e+000

+ -0.000000e+000 0.000000e+000

+ Rs = 1.569092e-003

+ 3.380801e-004 1.569092e-003

+ Gd = 7.910106e-012

+ -7.055706e-013 7.910106e-012

分析串擾時僅考慮互容與互感的影響，去掉Ro、Rs、Go和Gd的影響。所以把RLGC model修改成如下所示：

.MODEL Crosstalk W MODELTYPE=RLGC, N=2

+ Lo = 2.871471e-007

+ 5.941408e-008 2.871471e-007

+ Co = 1.049110e-010

+ -9.357921e-012 1.049110e-010

動態線信號參數設置： V1=1V， Tr= 1 ns， v = Len/Td，Td= 2 .592ns（動態信號延遲10 ns發送），由以上參數仿真得到的遠端串擾電壓如圖5所示。

圖 5 仿真得到遠端串擾波形

仿真得到的 Vcrosstalk-SIM=-1 66mV，計算得到的Vcrosstalk-CAL=-1 62mV。因為計算過程中所有的參數都認為是不變的，所有過程也都認為是線性的，所以計算結果和仿真結果略有差別，誤差小于2.5%。

5 結語

通過分析高速數字通信系統中單根傳輸線的 RLGC模型建立了兩根傳輸線之間的互容與互感等效串擾電路模型。通過分析模型上互容與互感的相互作用計算出遠端串擾噪音計算公式，并根據公式給出了減小高速數字通信系統中遠端串擾噪音的方法。為了證明推導公式的正確性最后使用HSPICE做了仿真驗證，公式的計算結果與仿真結果的一致性非常好的證明了推導公式的準確性。

[1] BOGATIN E. Signal Integrity： Simplified[M]. USA： Prentice Hall PTR, 2003.

[2] HALL S H, HALL G W, MCCALL J A. High-Speed Digital System Design：A Handbook of Interconnect Theory and Design Practices[M]. USA：John Wiley & Sons, Inc,2000.

[3] JOHNSON H, GRAHAM M. High-Speed Digital Design： A Handbook of Black Magic[M]. USA： Pearson Education Inc,1993.

[4] 黃志清, 王衛東,陳斌. 超寬帶通信技術抗部分頻帶干擾性能研究[J].通信技術,2009,42(12)：40-42.

[5] 肖振宇,金德鵬,曾烈光. 通信系統仿真中關于噪聲的分析與研究[J].通信技術,2009,42(04)：38-40.

[6] LEONEM. Design Expression for the Trace-to-edge Com-mon-mode Inductance of a PCB[J]. IEEE Trans. Elec-tromagn Compat, 2001,42(04)： 533-560.