流水線 CORDIC算法的 FPGA實現

王亞春, 蔡德林, 張夢龍, 王俊

(①安徽大學電子科學與技術學院,安徽 合肥 230039;②中國電子科技集團第 38研究所,安徽 合肥 200031)

0 引言

坐標旋轉計算機(CORDIC,Coordinate Rotational Digital Computer)算法是 Volder于 1959年在美國航空控制系統的設計中提出來的,它是一種用于計算運算函數的循環迭代算法。其基本思想是用一系列與運算基數相關的角度的不斷偏擺,從而逼近所需旋轉的角度,從廣義上講它是一個數值計算逼近的方法。這些固定的角度與計算基數有關,運算只有移位和加減,可通過該算法不同的實現模式(如圓周模式、雙曲線模式、線性模式等)來計算的函數包括乘、除、平方根、正余弦、反正切以及指數運算等。1971年,J.S Walther提出了統一的CORDIC算法形式,把圓周旋轉、雙曲旋轉和直線旋轉統一到同一個CORDIC迭代方程中,為同一硬件實現多功能運算奠定了基礎。在傳統的硬件算法設計中,乘、除等基本數學函數運算是一種既耗時又占用面積大的運算,CORDIC算法正是為解決這種問題而產生的,它從算法本身入手,將復雜的算法分解成一些在硬件中容易實現的基本運算,如加法、移位等,從而使得這些算法在硬件上可以得到較好的實現。

1 CORDIC算法的基本原理

以基于圓周模式的 CORDIC算法實現為例,介紹CORDIC算法的基本原理[1]。假設平面直角坐標系里有一向量：a(xi,yi)=a(r cosα,r sinα),現將其旋轉 θ角得到新向量：b(xj,yj)=b(r cos(α+θ),r sin(α+θ)),如圖 1所示,則有：

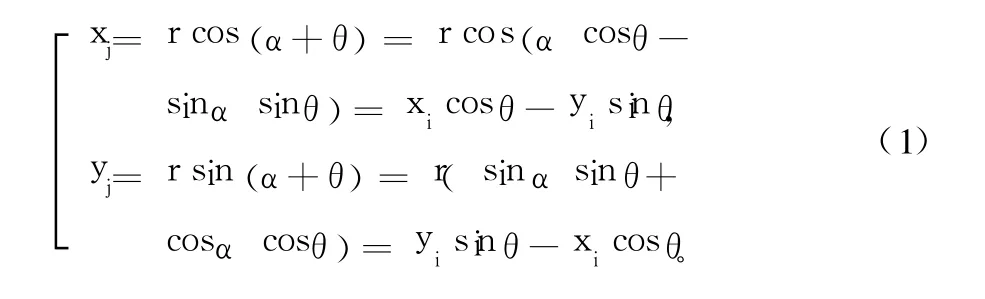
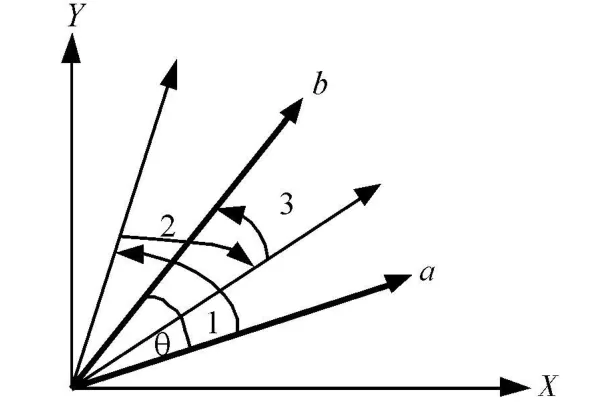
圖 1 CORDIC算法旋轉示意

寫成矩陣形式就是：

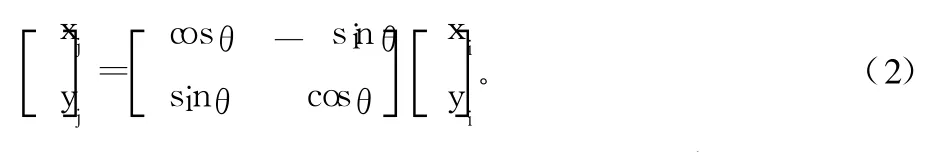
如果向量 a(xi,yi)經過 n次旋轉才到達 b(xi,yi),其中第 k次旋轉的角度為 θk,那么第 k次旋轉的表達式為：

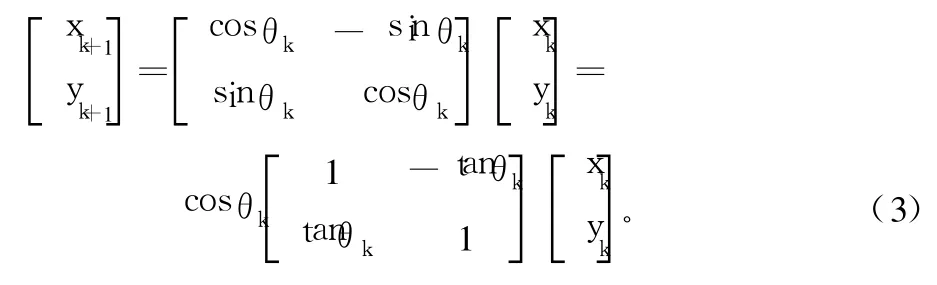
如果限制 tanθk=±2-k,則可以將 tanθk乘項的乘法操作變為移位操作,式(3)將只有一個乘積項 cosθk：

θk=Skarctan 2-k,Sk={-1,+1}。

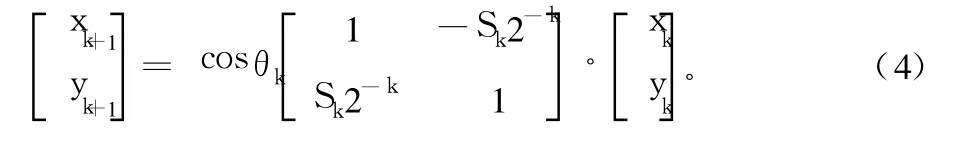
除了 cosθk系數外,CORDIC算法只需要簡單的移位和相加操作即可完成。事實上 cosθk還可以事先算出來。考慮到：

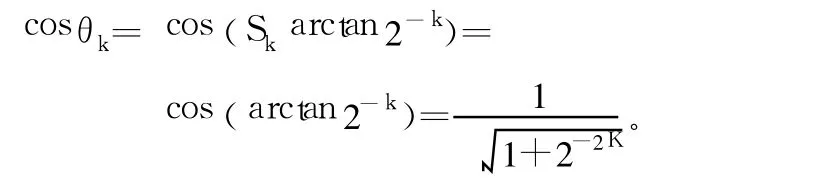
經過無數次迭代后,cosθk系數項將變成一個常數。由于 cosθk系數項是一個常數,因此可以在迭代的過程中忽略cosθk系數項,迭代的最后再將其乘入。這樣迭代式就變為：

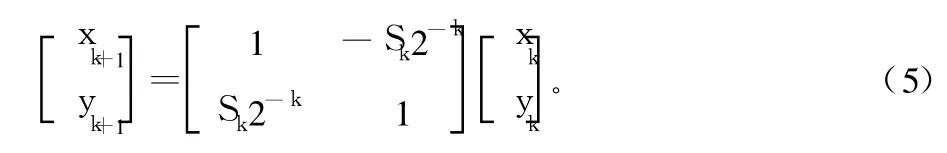
式(5)就是 CORDIC算法的迭代式。假設 z代表的是尚未旋轉的角度：

zk+1=(總角度 -已旋轉角度)=zk-Skarctan 2-k(未旋轉角度-剛旋轉角度),將此式和式(5)結合就得到了下面三個迭代方程式：其中 Sk的符號由第 k次旋轉時候的角度 zk決定,它們的關系是：Sk=-1,zk＜0

+1,zk≥0,向量 a(xi,yi)向向量 b(xj,yi)逼近的精度由迭代的次數決定,迭代的次數越多,逼近的精度就越高,迭代 n次(n→∞ )得到的最終結果為：

其中zn=0表明旋轉到了指定的角度。

2 CORDIC流水線結構的 FPGA實現

CORDIC流水線結構的 FPGA實現參考文獻[2-4]。在實際應用中,CORDIC的實現方式應該根據目標需求,在速度和資源之間進行折中。采用流水線結構,這種方式能夠在執行進程的同時輸入數據,從而極大提高了程序的運行效率,在該結構中,每一個移位器都是固定的深度,而且旋轉角度集的各個值作為常數直接連接到累加器上,不需要存儲空間和讀取時間,圖 2是CORDIC算法的一般流水線結構。

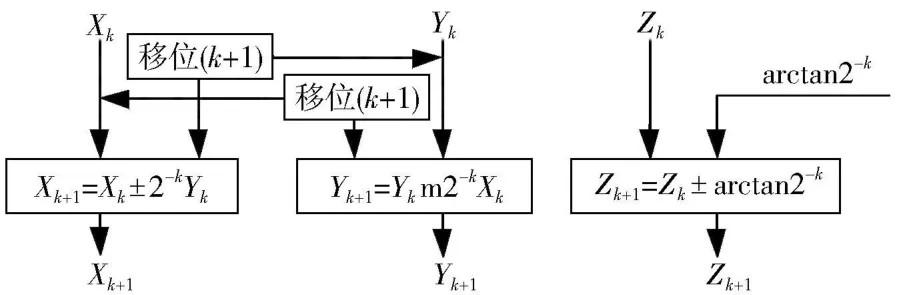
圖 2 CORDIC算法的一般流水線結構

3 仿真結果與分析

仿真結果與分析參考文獻[5]。該設計中選用的FPGA芯片是 Altera公司 CycloneⅢ系列中EP3C25F256C6器件,使用 VHDL語言完成電路描述之后,在QuartusⅡ軟件平臺上進行編譯、仿真的結果如圖 3所示(表 1列出其計算結果)。

圖 3 用FPGA實現CORDIC算法的時序仿真

其中輸入信號有兩個,分別為時鐘 clk和要計算的角度Angle。輸出則有 3個,分別是 x_out(余弦值)、y_out(正弦值)和 z_out(迭代結束時的角度誤差)。由式(7)可知,為了使最后結果中 x_out和 y_out分別為余弦值和正弦值,就應該設置 xi和 yi的初始值分別為 1/An和 0。但程序里的初始值并不是這樣設置的,這是因為把第一次迭代精簡在了初始值中設置,同時還進行了預處理,即擴大了輸入角度的范圍。圖 3仿真結果中,輸入角度Angle用十六進制數表示,計算出的正弦值y_out和余弦值 x_out則用帶符號整數表示。 無論是輸入角度 Angle還是輸出的正、余弦值均擴大了 215倍,實際的角度和計算結果應該除以 215。表 1列出了圖 3的仿真結果中的 4個角度和CORDIC計算結果,同時還列出了理論的正弦值和余弦值。可以看出,經過 16次迭代后,CORDIC計算結果已經非常精確。

表 1 CORDIC計算結果與理論值的比較

4 結語

探討了 CORDIC算法的一種硬件實現,它具有速度快、精度高、結構簡單易實現等優點,從實驗結果來看,其誤差很小,能夠滿足速度和精度的要求,因而具有十分重要的工程研究和應用意義。

[1]VOLDER JE.The CORDIC Trigonometric Computing Technique[J].IRE Trans.Electronic Computers,1959(EC-8)：330-334.

[2]徐光輝,程旭東,黃如,等.基于 FPGA的嵌入式開發與應用[M].北京：電子工業出版社,2006.

[3]田耘,徐文波,張延偉,等.無線通信 FPGA設計[M].北京：電子工業出版社,2007.

[4]UWE M B.數字信號處理的 FPGA實現[M].北京：清華大學出版社,2006.

[5]徐小峰,唐治德,鄧玉娟,等.基于 CORDIC算法的 QAM調制器的 FPGA實現[J].通信技術,2008,41(09)：9-11.