基于Kriging模型抗冰海洋平臺管節點疲勞可靠性研究

宋曉杰, 黃 一, 張 崎

(1.大連理工大學,大連 116011;2.大連理工大學船舶工程學院,大連 116023)

基于Kriging模型抗冰海洋平臺管節點疲勞可靠性研究

宋曉杰1, 黃 一2, 張 崎2

(1.大連理工大學,大連 116011;2.大連理工大學船舶工程學院,大連 116023)

以渤海冰情和冰荷載現場觀測數據為基礎,建立JZ20-2NW海域錐體模型冰力譜。同時利用譜分析方法,對該平臺進行冰激疲勞分析。并結合冰疲勞環境荷載及冰力譜函數,提出了相對于冰速、冰厚隨機冰載的管節點熱點應力幅的近似計算方法——Kriging插值方法。結果表明,Kriging插值方法及疲勞可靠性分析方法合理有效。

導管架平臺;冰激振動;譜分析;疲勞可靠性;Kriging模型

Abstract:The ice-force spectrum of pyramidal model for J Z20-2NW platform in its sea area is established based on ice conditions in the Bohai and the observational field data of ice load.At the same time,the ice-induced fatigue of platform is analyzed with spectrum analysis method.According to the ice fatigue load environment and the ice-force spectrum function,this paper puts forward an approximate calculation method of the tubular joints’hot spot stress range relative to ice velocity and thickness of stochastic ice load,which called Kriging interpolation.The results show that the Kriging interpolation and the analysis method of fatigue reliability are reasonable and effective.

Key words:jacket platform;ice-induced vibration;spectrum analysis;fatigue reliability;Kriging model

0 引言

海洋平臺是一種海洋工程結構物,它為開發和利用海洋資源提供了海上作業與生活的場所。

高緯度海域海冰對結構作用是結構設計和安全運營時需要考慮的重要因素。目前,渤海海洋平臺在交變冰力作用下平臺動力響應引起的管節點疲勞等問題越來越突出。有事實表明[2,3],只要有少數幾個管節點發生疲勞破壞就可能導致整個平臺的破壞。

本文基于疲勞可靠性分析方法,力求考慮更多的不確定影響因素,以對導管架平臺在疲勞方面的安全性作出比確定性方法更加合理的評估。

1 隨機冰載作用下海洋平臺管節點的熱點應力計算

1.1 頻域法確定熱點應力幅值

頻域法亦稱譜疲勞分析方法[5,6],考慮荷載隨機特性采用統計理論表述工況。假定冰載荷在短時間內是各態歷經、窄帶平穩的正態過程,根據應力循環轉換的觀點,結構的應力分布為窄帶隨機正態過程,其峰值服從瑞利分布。

岳前進等利用多年累積的冰力數據,對冰力進行譜分析工作,得到錐體冰力譜函數[1]:

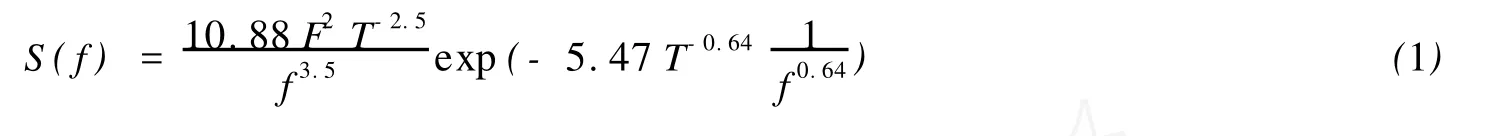
1.2 相對冰速、冰厚隨機冰載的熱點應力幅

由式(1)可看出,冰力譜函數與冰速、冰厚有關[7,8],而冰速、冰厚在冰期內是隨機變化的。要進行隨機荷載下的海洋平臺疲勞可靠性分析,需要計算大量冰況組合下的管節點熱點應力幅,但計算量很大。因此,本文提出基于 Kriging方法近似計算熱點應力幅[10,11]:(1)選擇一系列有代表性的冰厚和冰速冰況組合,對海洋平臺進行譜分析,計算出相對應的熱點應力幅;(2)根據已知的樣本點信息建立無偏的 Kriging模型;(3)利用 Kiging模型插值計算整個疲勞環境的熱點應力幅值。

2 冰振下海洋平臺管節點疲勞可靠性分析[7,8]

疲勞可靠性分析的最終目的是要從概率的角度對結構的疲勞壽命進行預測,從而對結構在疲勞方面的安全性作出評估[5]。海洋平臺管節點疲勞安全性的度量是計算所得的疲勞壽命 Tf大于等于設計壽命TD的概率,即 Pr=P(Tf≥TD)。對于船舶及海洋工程結構,設計壽命通常取為20年或25年。

2.1 海洋平臺疲勞壽命計算

疲勞壽命分析計算采用累積損傷模型,其以S-N曲線和Miner法則作為基礎[9]。在船舶及海洋工程結構疲勞可靠性分析中應用最為廣泛的是Wirsching模型[12,13]。

對比手術病理證明結果與MR檢查結果，計算診斷正確率、良性診斷符合率以及良惡性鑒別準確率，并對不同病變性質的信號特征進行總結。

疲勞累積損傷: D=NTE(Sm)/A(2)式中 NT為環循環次數總和。

設Sa為構件的應力幅,S為計算得到的應力幅,則有式中B是應力計算誤差因子,屬于隨機變量。

定義應力循環的平均頻率: f0=NT/T(4)

則有 D=TBmΩ/A (5)

這里定義Ω為應力參數,并且

不同的計算模型,對應著不同的Ω。

可得到疲勞壽命為 T=ΔA/(BmΩ)(7)

2.2 結構疲勞可靠度計算的對數正態格式

由上(7)式知疲勞壽命:T=ΔA/(BmΩ)

由于Δ、K、B是隨機變量,T也是隨機變量,疲勞失效概率為

式中:σlnT為lnT的標準偏差;為 T的平均值;TD為設計壽命。

應用對數正態分布法,即假定每一隨機變量服從對數正態分布。根據對數正態分布的特性,則有:(10)

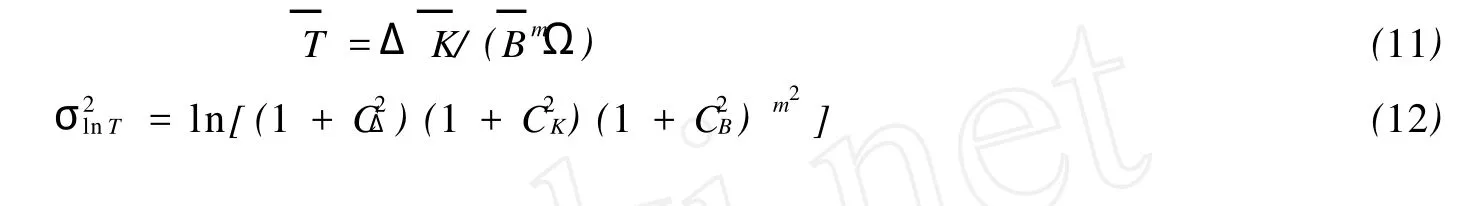
式中Ci為變量的變異系數。

3 J Z20-2NW平臺管節點疲勞可靠性分析

以渤海石油公司J Z20-2NW平臺為例,在疲勞環境中取一個45°的冰力方向,在冰速0～100 cm/s范圍內,平均選取41種冰速;在冰厚0～45 cm范圍內,平均選取41種冰厚。S-N曲線采用A PI-X曲線。相關數據參考相關文獻[5～9]。

選取有代表性的300種工況,利用ANSYS軟件對海洋平臺結構進行譜分析,最大節點應力均出現在兩個斜撐的交叉處,計算出對應的熱點應力幅值S。

根據上述建立的 Kriging模型計算待測點的響應。在此過程中實現了MATLAB軟件與ANSYS軟件的互相調用,共插值得到1 681種組合工況的結果。

程序運行結果如圖1所示。

為了驗證插值近似熱點應力計算的精度,在冰速為0～100 cm/s、冰厚為0～45 cm范圍內,每間隔3.4 cm取一種冰厚,共13種冰厚;每間隔7.7 cm/s取一種冰速,共13種冰速,共有169種組合工況。

依據得到的結果統計得出:在給定的冰況條件下,Kriging插值計算得到的近似結果與ANSYS譜分析得到的計算結果基本吻合,二者誤差小于1%,且隨著冰厚的增加,誤差遠低于1%。

李剛等提出的二次項擬合的近似計算熱點應力幅值的方法得到的誤差為4%。

在運算時間方面,在同一個計算機上,運行編制的ANSYS譜分析程序,完成一種工況計算需要10分鐘。而運行編制的基于Matlab的 Kriging插值程序,幾秒鐘即可完成所有工況計算。

根據上述情況,現用對數正態格式對J Z20-2NW平臺管節點的疲勞壽命進行可靠性預測。

設在每一工況中應力范圍的短期分布采用Rayleigh分布模型,規定的設計壽命為 TD=20年。S-N曲線采用A PI-X曲線。

隨機變量Δ和B的中值和變異系數等有關數據分別為

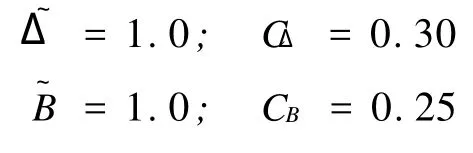
首先計算應力參數Ω。

圖1 近似計算得到的熱點應力

4 結論

本文結合現有的冰疲勞環境荷載及冰力譜函數,建立了相對于冰速、冰厚隨機冰載的等效應力幅值的計算方法,并利用對數正態格式計算了平臺結構的疲勞可靠性。本文提出的基于 Kriging模型的插值熱點應力的近似計算方法在保證精度的情況下,大大提高了計算效率,有明顯的優越性。且非線性關系越顯著,此種方法的優越性越明顯,較一般的單一設計冰厚的計算方法更加精確。該方法不僅可用于構件,也可用于海洋平臺系統整體的疲勞可靠性計算,從上述結果可看出,J Z20-2NW平臺有較高的可靠度。

[1] 劉圓.抗冰海洋平臺動力分析與結構選型研究[D].大連:大連理工大學,2007.

[2] 李剛,張大勇,岳前進.冰區海洋平臺的時變疲勞可靠性分析[J].計算力學學報,2006,23(5):513-517.

[3] API RP 2N.Recommended practice for planning,designing and constructing fixed offshore structures in ice environments[S].1988.

[4] API RP 2N.Recommended practice for planning,designing and constructing fixed offshore structures[S].1991.

[5] 趙國藩,金偉良,貢金鑫.結構可靠度理論[M].北京:中國建筑工業出版社,2000.

[6] 錢進.導管架平臺疲勞可靠性分析[D].南京:河海大學,2006.

[7] Wirsching P H.Fatigue of offshore structures[M].Journal of Structural Engineering,American Petroleum Institute.PRAC Project 81-15,1983.

[8] Wirsching P H,Wu Y T.Probabilistic and statistical methods of fatigue analysis and design[J].Pressure Vessel and Piping Technology,A Decade of Progress,ASME,1985,793-819.

[9] 陳傳堯.疲勞與斷裂[M].武漢:華中科技大學出版社,2002.

[10] 翟進乾.克里金(kriging)插值方法在煤層分布檢測中的應用研究[D].太原:太原理工大學,2008.

[11] 曾懷恩,黃聲享.基于 Kriging方法的空間數據插值研究[J].測繪工程,2007,16(5):5-8,13.

[12] 方華燦,許發彥.渤海平臺構件疲勞分析的新方法[J].石油學報,1997,18(4):95-100.

[13] 方華燦,陳國明.冰區海上結構物的可靠性分析[M].北京:石油工業出版社,2000.

[14] Shimokawa T,Tanaka S.A statistical consideration of Miner’s rule[J].International Journal of Fatigue,1980,2(4):165-170.

[15] Martindale S G,Wirsching P H.Reliability-based progressive fatigue collapse[J].Journal of Structural Engineering,ASCE,1983,109(8):1792-1811.

[16] ABS.Guidance notes on spectral-based fatigue analysis for floating offshore structures[S].March,2005.

Study on Fatigue Reliability Analysis of Tubular Joints for Ice-Resistant Offshore Platform Based on Kriging Model

SONG Xiao-jie1, HUANG Yi2, ZHANG Qi2
(1.Department of Continuing Education,Dalian University of Technology,Dalian 116011,China;2.Department of Naval Architecture,Dalian University of Technology,Dalian 116023,China)

O346.5

A

1001-4500(2010)01-0032-04

2009-03-23; 修改稿收到日期:2009-09-30

宋曉杰(1983-),女,碩士生,從事船舶與海洋工程結構分析。