正壓流體中具有β效應與地形效應的強迫Rossby孤立波*

宋健 賴俊峰

(內蒙古工業大學理學院數學系，呼和浩特010051)

(2009年10月16日收到;2009年10月28日收到修改稿)

正壓流體中具有β效應與地形效應的強迫Rossby孤立波*

宋健 賴俊峰?

(內蒙古工業大學理學院數學系，呼和浩特010051)

(2009年10月16日收到;2009年10月28日收到修改稿)

正壓流體中，從有外源的準地轉位渦方程出發采用攝動方法和時空伸長變換推導了具有β效應、地形效應和外源的強迫Rossby孤立波方程，得到孤立Rossby波振幅的演變滿足帶有地形與外源強迫的非齊次Boussinesq方程的結論.通過分析孤立Rossby波振幅的演變，指出β效應、地形效應以及外源都是誘導Rossby孤立波產生的重要因素，說明在地形強迫效應和非線性作用相平衡的假定下，Rossby孤立波振幅的演變滿足非齊次Boussinesq方程，給出在切變基本氣流下地形和正壓流體中Rossby波的相互作用.

非齊次Boussinesq方程，β效應，地形，外源

PACC:4735，0340K

1. 引言

地球物理流體中，Rossby波是指生命史很長結構上有組織的前后一致的大尺度永久性波動，并且這些波動具有穩定的、大振幅孤立波特征.對于正壓流體，Long［1］在1964年做了開創性的研究，得到在β平面近似下Rossby波振幅演變滿足Kortewegde Vries(KdV)方程，Benney［2］在1966年推廣了Long的結論，同時還得到Rossby孤立波波速與波振幅有關的結論，刻畫了非線性的重要性.Larsen［3］和Clarke［4］也研究了Rossby孤立波振幅的演變，他們得到了一系列與文獻［1］類似的結果.Redekopp［5］和Wadati［6］從正壓流體和分層流體的模式推導了Rossby孤立波振幅演變的方程分別滿足KdV方程和改進的KdV(mKdV)方程的結論，極大地推廣了文獻［1］的結果.Redekopp等［7］研究了切變氣流中Rossby孤立波的產生，指出在緯向流中Rossby孤立波存在的必要條件.Maslowe等［8］討論了在分層流體中緯向流切變對Rossby波的影響.Charney和Straus［9］基于準地轉位渦度方程構造了一個β平面通道中考慮地形、非絕熱加熱和摩擦的正壓大氣模式，這項工作開創了大氣多平衡態非線性動力學的研究［10］.Boyd［11，12］用多重尺度方法，從基本方程導出在正壓流體中小振幅Rossby孤立波振幅演變滿足非線性KdV方程和mKdV方程.劉式適和譚本馗［13］研究了Rossby參數隨緯度的變化，羅德海［14，15］用推廣的β平面近似模式研究了Rossby孤立波和β隨緯度變化的關系，得到β隨緯度變化可能是偶極子阻塞的原因.趙強［16］討論了地形對熱帶大氣超長尺度Rossby波的影響，指出了地形隨緯度的變化能夠導致熱帶大氣超長尺度Rossby波波動的不穩定.Meng等［17］利用擾動展開和時空伸長變換導出了包括地形和外源的非齊次Boussinesq方程，討論了近共振地形強迫Rossby孤立波的產生，顯示出地形對擾動具有明顯的增幅作用.達朝究和丑紀范［18］研究了地形隨時間緩變時Rossby波振幅的演變問題.宋健和楊聯貴等［19—22］在正壓流體與層結流體中分別給出β效應與地形效應對Rossby孤立波振幅的影響，張亮等［23］給出了正壓Rossby波擾動能量問題，汪萍和戴新剛［24］討論了外強迫作用下正壓大氣非線性特征數值模擬，說明了大氣大尺度非線性運動的某些特征.孤立波解在非線性問題中占有重要地位，給出了許多求孤立波解的方法［25—29］，如Hirota雙線性方法［30］、橢圓函數展開法［31，32］等被廣泛應用.本文在基本氣流有切變的條件下研究了β平面近似與非線性地形變化及其外源對Rossby孤立波振幅的演變.

2. 方程的推導

2.1. 控制方程與邊界條件

考慮有地形和外源無量綱形式的準地轉位渦方程［17，33，34］

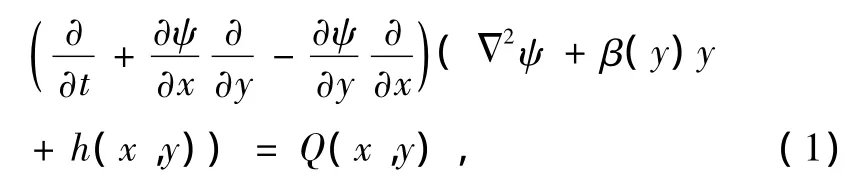
方程(1)中，ψ是流函數，2為Laplace算子，定義為

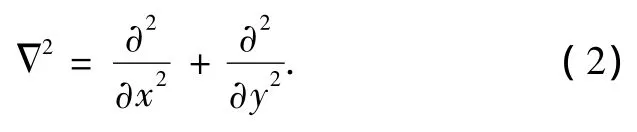
β平面近似取為β(y)y，即β是緯度變量y的函數［19—22］，h(x，y)，Q(x，y)分別是地形廓線和外源.

側邊界條件為剛壁條件的無量綱形式，取

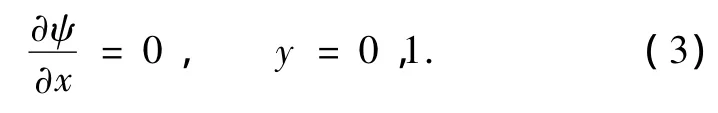
2.2. 帶有強迫項的非齊次Boussinesq方程

取基本流函數為緯向流

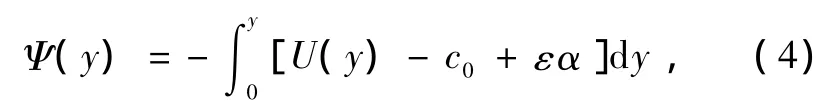
總的流函數

其中ψ′是擾動流函數，將(5)式代入方程(1)與邊界條件(3)同時略去擾動流函數的撇號，得到擾動流函數的方程及邊界條件

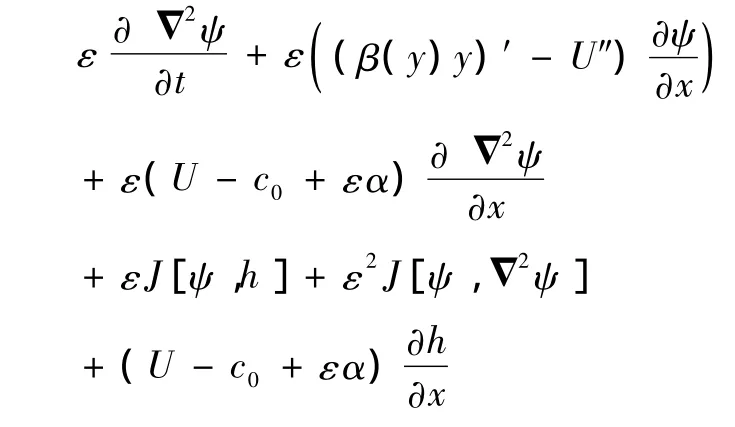
式中(β(y)y)′是β(y)y對變量y的一階導數，U″是U(y)對變量y的二階導數，是Jacobi算子.

邊界條件為

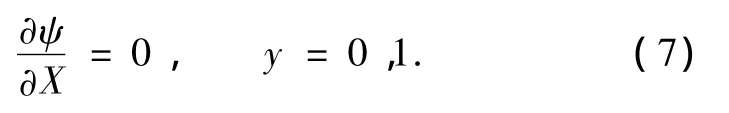
為了使方程(6)中的非線性效應與頻散項相平衡，對變量x，t引進緩變坐標

并且假設

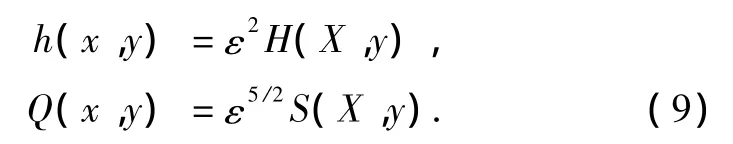
將(8)，(9)式代入方程(6)，(7)得到

上述方程中已沒有快變量x，t，只有緩變量X，T，為了表示方便引進兩個微分算子

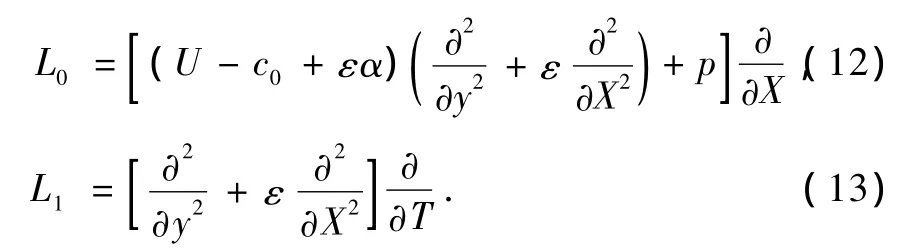
(12)式中p=(β(y)y)′－U″，這樣方程(10)可以寫為

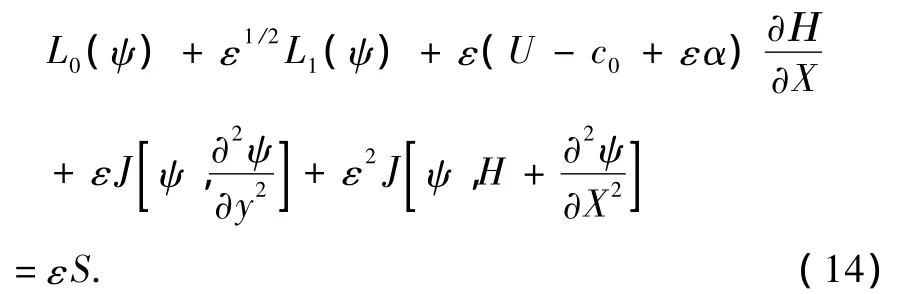
假設擾動流函數有如下的小參數展開形式［35］:

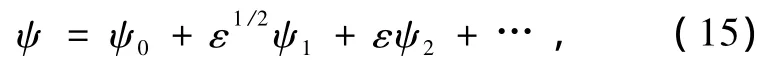
將(15)代入方程(14)和邊界條件(11)，并應用兩個微分算子L0，L1，得到各階攝動問題的方程與邊界條件.

對于O(ε1)階，有

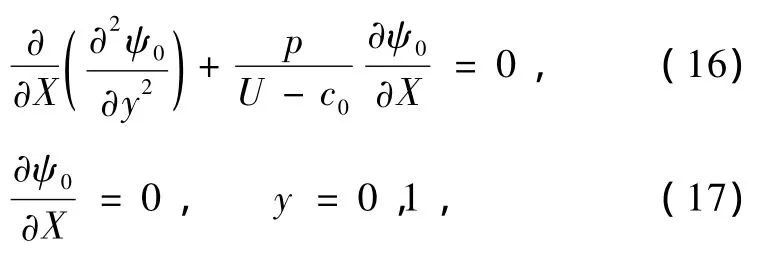
方程(16)中已假設U－c0≠0.

假設ψ0有如下形式的分離變量解:

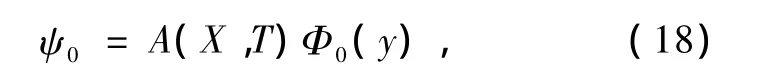
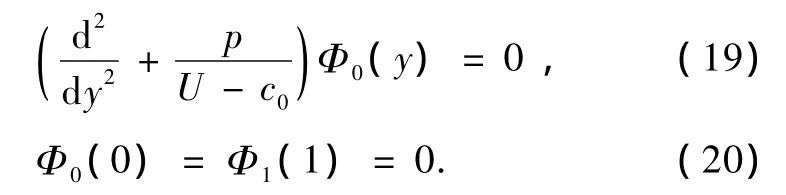
(19)，(20)式構成一個本征值問題，從該本征值問題中能夠確定本征函數Φ0(y)與本征值c0，對于確定的p(y)，Φ0(y)就能被確定.由于p(y)是關于緯度變量y的非線性函數，方程(19)，(20)很難獲得解析解.另外，在本階問題中，只能確定波的空間結構，而不能確定波振幅隨時間的演變.為了確定波振幅A(X，T)的演變，繼續求解高階問題.

對于O(ε2)階，有

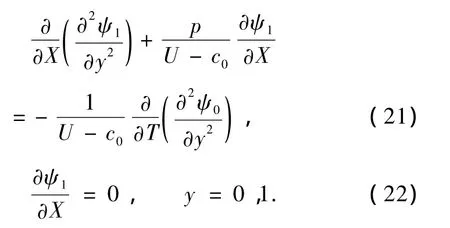
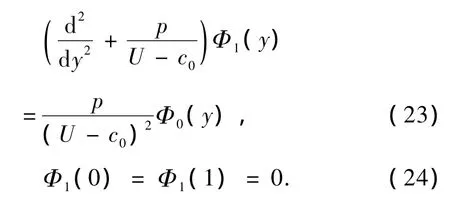
為了得到Rossby波振幅的數學模型，我們繼續求解更高階的問題.

對于O(ε3)階，有

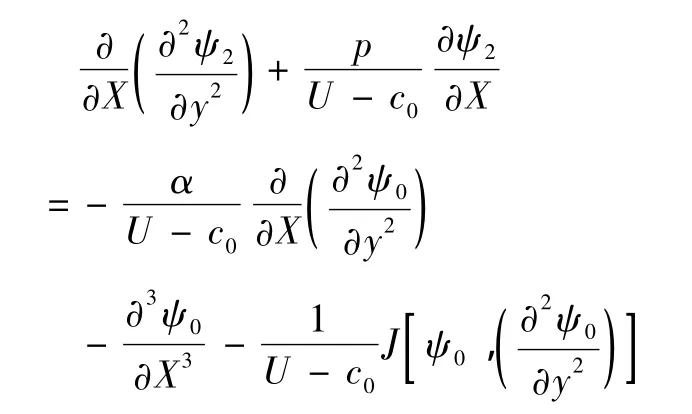
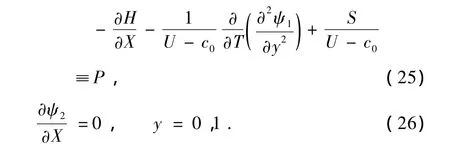
以農村污染治理為例。我國當前的環境保護工作對于工業和城市污染的重視程度要遠高于對農村污染的防治,雖然這兩年中央加大了對農村污水和垃圾等問題的投入,但農村污染防治工作還遠不到位。對于農村污染防治工作這個短板,未來首先需要解決的就是環保部和相關部門應盡快出臺全面的頂層設計和部署,將農村環境污染防治工作作為鄉村振興計劃的重要組成部分加以統籌規劃。

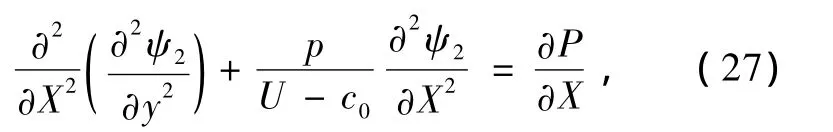
將ψ0=A(X，T)Φ0(y)以及方程(19)，(23)代入方程(27)的右端得

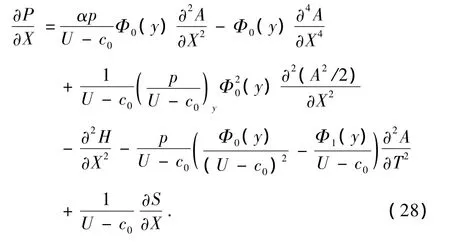
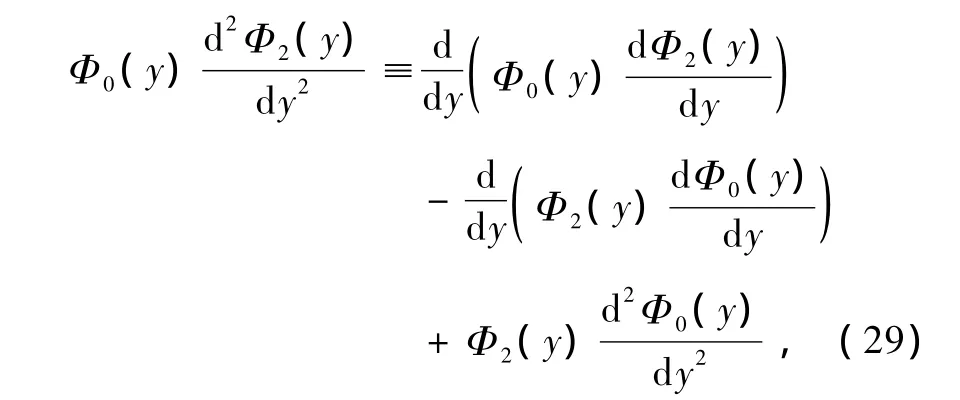
得到消奇異條件

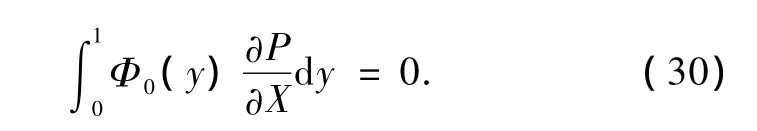
這表明，若攝動問題(15)式有效，P必須滿足方程(30)，否則將出現無窮大振幅的奇異效應，即共振現象.將(28)式代入方程(30)，有

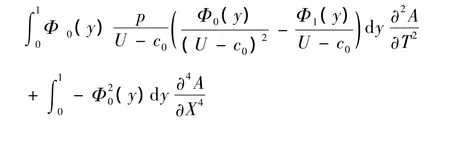
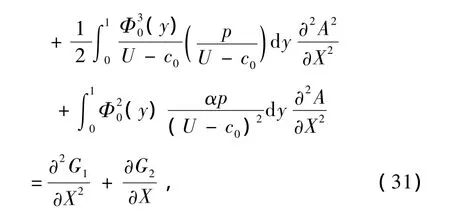
若記

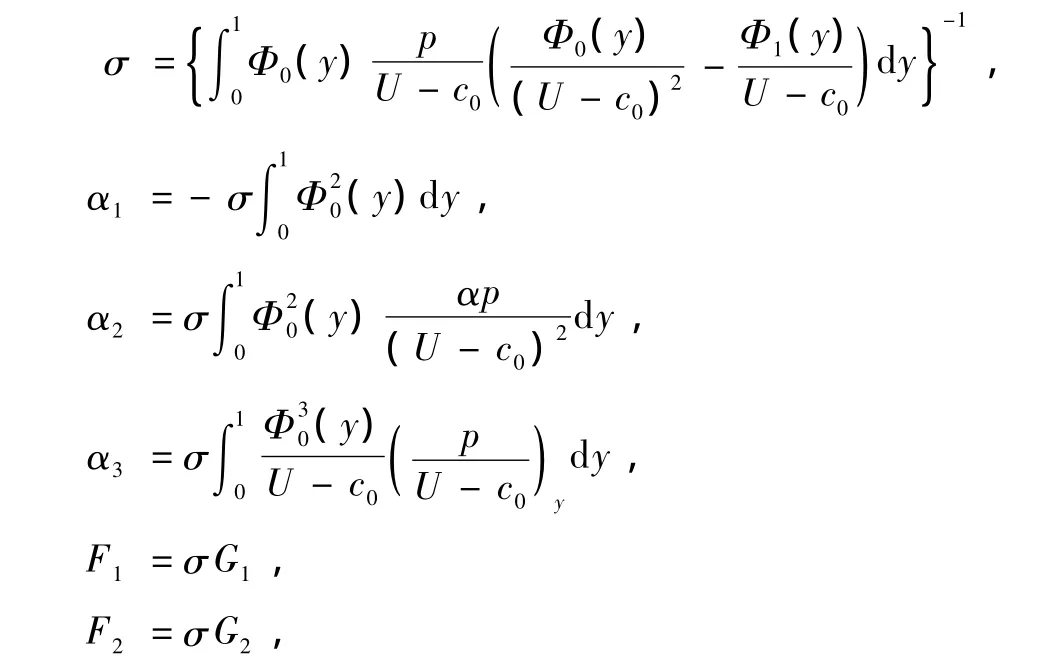
這樣，方程(31)可簡寫為

方程(32)說明正壓流體中Rossby孤立波振幅的演變滿足非齊次Boussinesq方程，系數α1，α2，α3依賴于函數β(y)，U(y).F1與地形廓線H(X，y)有關，F2與外源S(X，y)有關，如果F1，F2為常數，即不存在地形效應和外源，此時方程(32)是齊次Boussinesq方程，其孤立波解

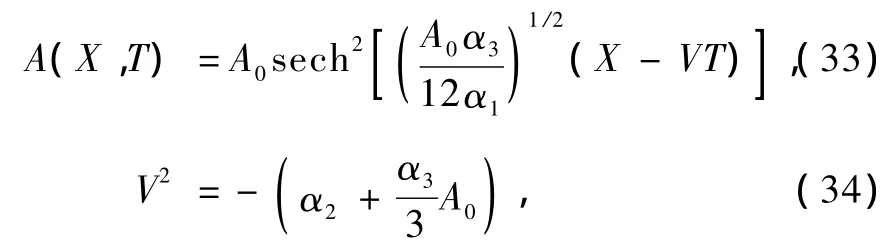
其中A0是初始孤立波振幅，(34)式顯示了孤立波向兩端傳播.方程(32)說明β(y)，U(y)，地形H(X，y)和外源S(X，y)能夠誘導Rossby孤立波.此外，由(31)式可以看出，孤立波的存在還必須滿足

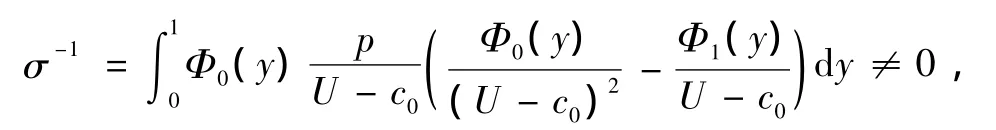
這表示不能產生正壓不穩定［36］.事實上，一旦產生正壓不穩定，就不可能保持恒定波型了.

3. 結論

正壓流體中，應用攝動法導出了Rossby孤立波振幅的演變滿足非齊次Boussinesq方程，當基本氣流有切變，非線性β效應、地形效應以及外源都是Rossby孤立波產生的重要因子.

［1］Long R 1964 J.Atmos.Sci.21 197

［2］Benney D J 1966 J.Math.Phys.45 52

［3］Larsen L N 1965 J.Atmos.Sci.22 222

［4］Clarke A 1971 Geophys.Fluid Dyn.2 343

［5］Redekopp L G 1977 J.Fluid Mech.82 725

［6］Wadati M 1973 J.Phy.Soc.Japan 34 1289

［7］Redekopp L G，Weidman P D 1978 J.Atmos.Sci.35 790

［8］Maslowe S A，Redekopp L G 1980 J.Fluid Mech.101 321

［9］Charney J G，Straus D M 1980 J.Atmos.Sci.37 1157

［10］Feng G L，Dong W J，Jia X J，Cao H X 2002 Acta Phys.Sin. 51 1181(in Chinese)［封國林、董文杰、賈曉靜、曹鴻興2002物理學報51 1181］

［11］Boyd J P 1980 J.Phys.Oceanogr.10 1699

［12］Boyd J P 1983 J.Phys.Oceanogr.13 428

［13］Liu S K，Tan B K 1992 Appl.Math.Mech.13 35(in Chinese)［劉式適、譚本馗1922應用數學和力學13 35］

［14］Luo D H 1991 Acta Meteor.Sin.5 587

［15］Luo D H 1995 J.Appl.Meteor.6 220(in Chinese)［羅德海1995應用氣象學報6 220］

［16］Zhao Q 1997 J.Trop.Meteor.13 140(in Chinese)［趙強1997熱帶氣象學報13 140］

［17］Meng L，Lu K L 2000 Chin.J.Compu.Phys.17 259

［18］Da C J，Chou J F 2008 Acta Phys.Sin.57 2595(in Chinese)［達朝究、丑紀范2008物理學報57 2595］

［19］Song J，Yang L G，Da C J，Zhang H Q 2009 Atmos.Ocea.Sci. Letters 2 18

［20］Song J，Yang L G 2009 Chin.Phys.B 18 2873

［21］Song J，Yang L G 2010 Prog.Geophy.25 543(in Chinese)［宋健、楊聯貴2010地球物理學進展25 543］

［22］Song J，Yang L G 2010 Acta Phys.Sin.59 3309(in Chinese)［宋健、楊聯貴2010物理學報59 3309］

［23］Zhang L，Zhang L F，Wu H Y，Li G 2010 Acta Phys.Sin.59 44(in Chinese)［張亮、張立鳳、吳海燕、李剛2010物理學報59 44］

［24］Wang P，Dai X G 2005 Acta Phys.Sin.54 4961(in Chinese)［汪萍、戴新剛2005物理學報54 4961］

［25］Fan E G，Zhang H Q 1998 Acta Phys.Sin.47 353(in Chinese)［范恩貴、張鴻慶1998物理學報47 353］

［26］Fan E G，Zhang H Q 2000 Acta Phys.Sin.49 1409(in Chinese)［范恩貴、張鴻慶2000物理學報49 1409］

［27］Mao J J，Yang J R 2005 Acta Phys.Sin.54 4999(in Chinese)［毛杰健、楊建榮2005物理學報54 4999］

［28］Zhu H P，Zheng C L 2006 Acta Phys.Sin.55 4999(in Chinese)［朱海平、鄭春龍2006物理學報55 4999］

［29］Mo J Q，Zhang W J，Chen X F 2009 Acta Phys.Sin.58 7397 (in Chinese)［莫嘉琪、張偉江、陳賢峰2009物理學報58 7397］

［30］Mao J J，Yang J R 2007 Acta Phys.Sin.56 5049(in Chinese)［毛杰健、楊建榮2007物理學報56 5049］

［31］Liu S D，Fu Z T，Liu S K，Zhao Q 2002 Acta Phys.Sin.51 718(in Chinese)［劉式達、付遵濤、劉式適、趙強2002物理學報51 718］

［32］Liu S K，Fu Z T，Liu S D，Zhao Q 2002 Acta Phys.Sin.51 1923(in Chinese)［劉式適、付遵濤、劉式達、趙強2002物理學報51 1923］

［33］Patione A，Warn T 1982 J.Atmos.Sci.39 1018

［34］Warn T，Brasnett B 1982 J.Atmos.Sci.40 28

［35］Jeffrey A，Kawahara T 1982 Asymptotic Methods in Nonlinear Waves Theory(Melbourne:Pitman Publishing Inc.)pp256—266

［36］Kou H L 1949 J.Meteor.6 105

PACC:4735，0340K

*Project supported by the Foundation of the Education Department of Inner Mongolia，China(Grant Nos.NJZY08005，NJ09066)and the Science Research Foundation of Inner Mongolia University of Technology，China(Grant Nos.X200829，X200933).

?Corresponding author.E-mail:ljfimpu@sina.com

Forced solitary Rossby wave with beta effect and topography effect in barotropic flows*

Song Jian Lai Jun-Feng?
(Department of Mathematics，College of Sciences，Inner Mongolia University of Technology，Hohhot010051，China)
(Received 16 October 2009;revised manuscript received 28 October 2009)

For the barotropic fluid，based on the quasi-geostrophic potential vorticity equation，an inhomogeneous Boussinesq equation including topographic forcing and an external source is derived by employing the perturbation method and stretching transform of time and space.Through inspection of the evolution of the amplitude of the Rossby wave，it is found that Coridis effect，topography effect and an external source are the key inducing factors of the solitary Rossby wave if the basic stream function has a shear flow.Assuming that there is a balance between nonlinear and topography effects，an inhomogeneous Boussinesq equation is derived.The results show that the topography and the Rossby wave interact in the barotropic flow.The inhomogeneous Boussinesq equation describing the evolution of the amplitude of solitary Rossby waves with the change of Rossby parameter β(y)with latitude y，topographic forcing and the external source is obtained.

inhomogeneous Boussinesq equation，β effect，topography，an external source

book=395,ebook=395

*內蒙古教育廳基金(批準號:NJZY08005，NJ09066)和內蒙古工業大學科學研究基金(批準號:X200829，X200933)資助的課題.

?通訊聯系人.E-mail:ljfimpu@sina.com