蟻群算法在梯形明渠臨界水深計算中的應用

□ 劉思韜 王慧斌

一、引言

臨界水深是判別明渠流態的一個重要指標，也是明渠水力學中基本水力要素之一。不同形式的過水斷面，其臨界水深的計算方法有所不同。在工程中，梯形斷面臨界水深hk的計算最常采用的計算方程是一元六次方程，通常采用試算法、圖解法、近似公式法和迭代法計算，這些方法均具有計算量大、精度不高等缺點。因此，本文采用蟻群算法對梯形明渠臨界水深進行計算。

二、蟻群算法簡介

在優化領域，蟻群算法作為一類仿生計算方法正在迅速發展。蟻群算法由Dorigo等人提出，它具有開放性、魯棒性、并行性、全局收斂性等特點，適合求解諸如旅行商問題（Travelling Salesm an Problem,TSP）、車間調度、交通路由、資源分配、圖著色、大規模集成電路設計、通訊網絡中的路由問題以及負載平衡等問題。

由于梯形明渠臨界水深的計算屬于一維連續函數優化問題，因此，本文僅對一維連續函數優化的蟻群算法進行介紹。設一維連續函數優化的問題為：

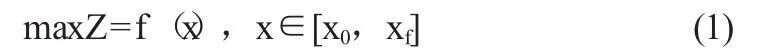
其中f（x）：R→R為已知的一維函數，[x0，xf]為實軸上的已知解空間。

為實現蟻群算法的群體搜索過程，構造如下的轉移概率準則：設m只人工螞蟻，剛開始隨機位于解空間[x0，xf]的n個等分區域的某些位置處，各個區域間螞蟻的狀態轉移概率定義為：

其中，τj為區域j的吸引強度；期望值ηij(啟發信息)定義為ηij=fjmax-fimax；參數α、β均為定值，其中α為吸引強度啟發式因子，β為期望值啟發式因子。區域j吸引強度的更新方程為：

于是函數f(x)的尋優問題就借助于m只螞蟻在x∈[x0,xf]的n個等分區域間的不斷地移動，以及一些區域內的局部隨機搜索來進行，處在區域i中的螞蟻k的轉移及其搜索規則為：

否則，在第i區域內進行隨機搜索

可見，每只螞蟻要么以上述規則從當前區域轉移到其它區域中作局部隨機搜索，要么在當前區域內進行局部隨機搜索。一旦螞蟻的群體數目足夠大，上述的尋優方式就相當于一群螞蟻對定義域[x0,xf]中的函數f(x)進行有窮盡的且在先驗知識引導下的隨機搜索，并最終收斂到問題的全局最優解。

三、梯形明渠臨界水深的計算

臨界水深計算的基本公式為：

式（6）中，α為動能修正系數；Q為過水流量；g為重力加速度；Ak為相應臨界水深的過水斷面；Bk為相應于臨界水深時的水面寬度。

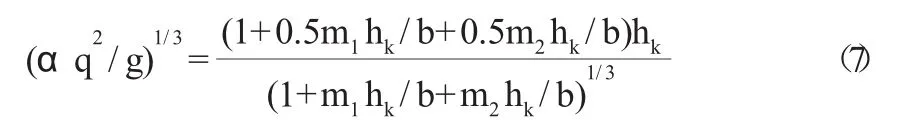
式（7）中，hk為臨界水深；b為梯形斷面底寬；單寬流量q=Q/b；m1,m2分別為梯形斷面兩側的邊坡系數。

求解梯形明渠臨界水深hk等價于求解下面非線性優化問題：

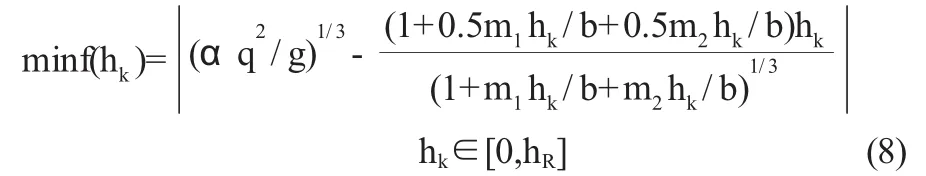
式(8)中，f(hk)優化目標函數；hk為優化變量；hR為與梯形斷面底寬相同的矩形斷面明渠的臨界水深。

為考察蟻群算法在梯形斷面明渠臨界水深計算問題上的優化性能，在此選取參考文獻[4]中的例1為算例（以便與其比較）：已知梯形明渠底寬b=10 m，梯形斷面兩側的邊坡系數m1=m2=1，動能修正系數α=1，重力加速度g=9.81 m2/s，求解臨界水深hk。將蟻群算法的優化結果與相振國等的近似公式法、金菊良等的加速遺傳算法（AGA）在該算例上的求解結果進行比較，判斷蟻群算法優化梯形斷面明渠臨界水深的性能。

在本文的蟻群算法中，有關算法參數的取值為：螞蟻在搜索中釋放的信息素密度Q=0.5，吸引強度持久性系數ρ=0.8，吸引強度啟發式因子α=1，期望值啟發式因子β=1，解空間分區數n=30，參與搜索的螞蟻數為m=40，求解結果見表1。

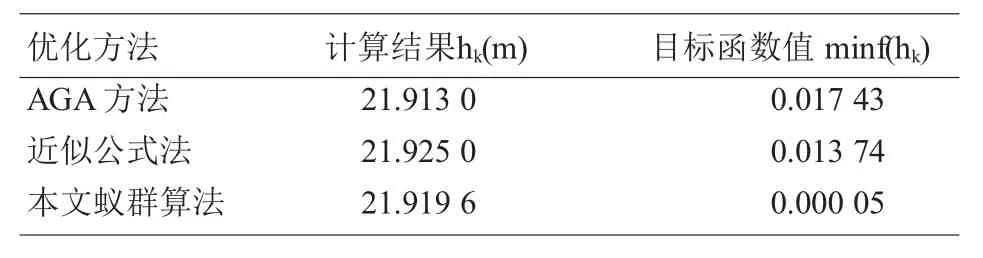
表1 采用不同方法計算梯形明渠臨界水深的結果比較

由表1可見，本文所選用的蟻群算法在求解梯形明渠臨界水深問題時，與加速遺傳算法（AGA）和近似公式法相比，可以得到全局最優解，并且蟻群算法適應性強，且易于形成通用的計算機程序，算法穩定，收斂速度快，因此總體效果優于加速遺傳算法和近似公式法。

四、結論

由本文的算例可知，蟻群算法是一種收斂速度快、算法穩健、計算過程簡單、易于形成通用的計算機程序的非線性全局優化方法。在求解梯形明渠臨界水深問題時，其優化效果明顯的優于傳統的近似公式法和加速遺傳算法，因此，可以將蟻群算法引用到水利工程中的梯形明渠臨界水深的計算中。除此之外，蟻群算法還可用于水利工程中的許多優化問題，如天然河道水面線的推求、溢流壩收縮斷面水深的計算等。蟻群算法將為水利工程的優化問題提供一種新的有效的優化方法。■