固支半球殼的隨機響應分析

李軍，冷小磊

固支半球殼的隨機響應分析

李軍*，冷小磊

（南京航空航天大學 振動工程研究所 飛行器結構力學與控制教育部重點實驗室，南京210016）

在經典薄殼理論的基礎上，采用數值計算分析了周邊固支半球殼的固有模態。算出了軸對稱自由振動固有頻率和用勒讓德函數表示的固有振型。在模態疊加法基礎上，給出了橫向激勵下系統的響應特性。最后結合隨機分析理論算出了殼體在橫向白噪聲激勵下的均方響應，并給出了殼體各點的穩態均方響應曲線和時變均方響應曲線。

球殼；隨機振動；均方響應

1 引言

殼體結構具有很好的空間傳力性能，廣泛應用于工程結構中。殼體結構在實際使用中，經常受到各種載荷的激勵，而這些激勵多是隨機的。因此，有必要研究殼體結構在隨機激勵下的隨機響應。而近一個世紀來，球殼振動問題，除了固有模態求解[1,2,7,13]，對于強迫振動，大多數限于研究確定性振動響應問題[3,5,6]。由于20世紀50年代人們才開始隨機振動的探討，因此有關隨機激勵下的半球殼的響應，目前可見的文獻中，還難以看到相關的研究成果。

對于連續系統的振動響應問題，通常的做法是先求出固有模態，并根據精度要求進行模態截斷，即將連續系統的響應轉化為前幾階模態響應的線性組合來研究。本文仍然采用上述傳統做法，采用文獻[1]的思想，借鑒了文獻[13]中的處理方法，算出了周邊固支半球殼的固有模態。然后結合模態疊加法[8]和隨機分析理論[10]，求出了殼體在橫向分布激勵下的響應特性，進一步算出了穩態白噪聲激勵下殼體的均方響應和突加白噪聲情況下殼體各點的時變均方響應。

2 半球殼固有模態的求解

考察周邊固支的半球殼，如圖1所示，其中φ、θ分別表示殼體任一點的經向角、緯向角，u、v、w分別表示該點處的經向位移、緯向位移和橫向（法向）位移。按照經典的勒夫薄殼理論，考慮殼

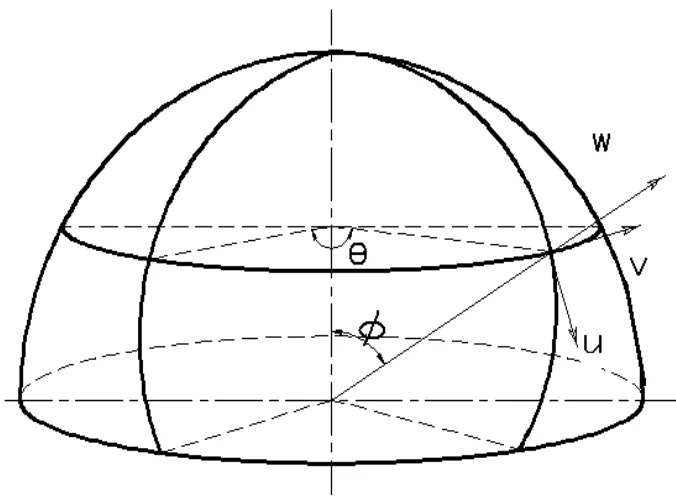
圖1 半球殼示意圖

體的薄膜剛度和彎曲剛度時，殼體的振動微分方程可以用下面的方程（1）、（2）來表示：[8]

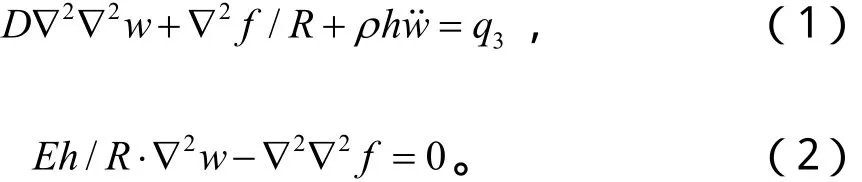
對于軸對稱情形，消去應力函數 f，結合分離變量法可得到關于橫向振型函數W的方程[9]。

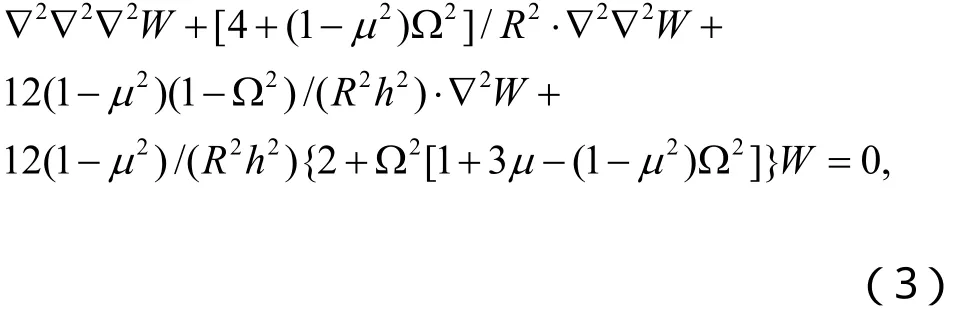
3 橫向穩態隨機白噪聲激勵下的殼體均方響應求解

求出系統的固有模態后，根據模態疊加法，殼體的響應可寫為：

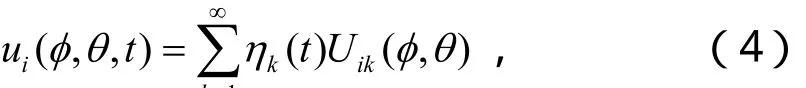
式中，ui（i=1，2，3）是位移響應在經向（u）、緯向(v)和橫向(w)三個主方向的上的分量，Uik是第 k階固有振型在三個主方向的上的分量，模態坐標ηk(t)是未知的待定函數。模態坐標 ηk(t)的方程可以寫為（具體推導可以參見文獻[8]）：

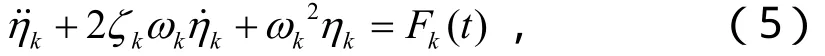
式中：

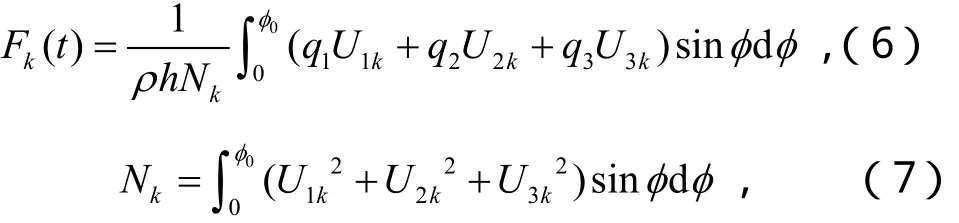
ζk稱為模態阻尼系數，q1、q2、q3表示激勵在三個主方向上的分量。由于本文只考慮軸對稱情況，U2k和q2為零，U1k和U3k只和φ有關。在不引起混淆的情況下，下文中縱向位移U1k用Uk表示，橫向位移U3k用Wk表示。

考察殼體只受橫向均勻分布激勵的情況下，方程（5）可以寫為：

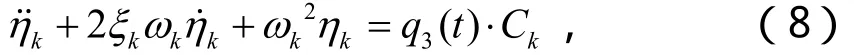
由方程（8），可以求出模態坐標 ηk(t)對橫向均勻分布激勵的頻響函數。再結合方程（4）可以直接求出系統在橫向激勵下的頻響函數H(φ, ω)：

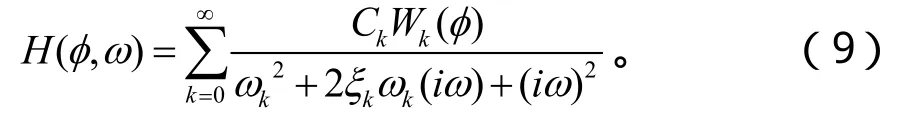
對于平穩隨機激勵，如果已知殼體各點受到的激勵的功率譜密度，就可以根據隨機振動理論求出系統位移的均方響應【10】。

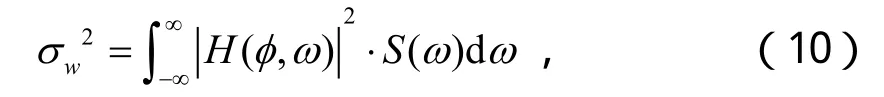
這樣，知道了隨機激勵的功率譜密度，通過上述公式可以很方便地求出殼體任一點處的位移均方響應。由于本模型的支撐條件為軸對稱（周邊固支），載荷也為軸對稱（橫向均勻分布激勵），所以響應也必為軸對稱，即半球殼的響應可以用任意一條經線上的響應來表示。在均勻分布橫向白噪聲激勵的功率譜密度為 S(ω) = 106kg2/m2/s3時，殼體位移均方響應隨φ的變化如圖2所示。

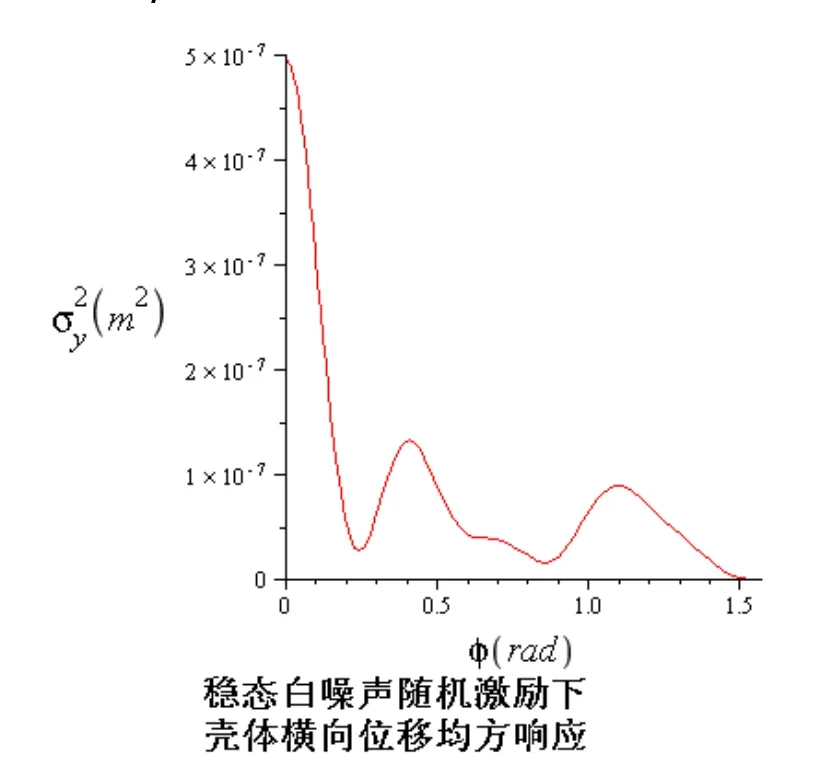
（圖2）

從圖2中可以看出，在穩態白噪聲激勵下，殼體中心對稱點的均方響應遠大于殼體其他各點。而除了中心對稱點，在緯向角大約0.4弧度和1.1弧度所對應的圓上，各點的均方響應也比鄰近的點的均方響應要大。

4 橫向突加白噪聲隨機激勵下殼體的時變均方響應

上面求出了殼體上各點在隨機平穩白噪聲橫向激勵下的穩態位移均方響應，對于殼體在突加白噪聲激勵下的時變位移均方響應，本文按虛擬激勵法進行求解。假設方程（5）中，各模態響應的初始條件為 ηk(0) =η˙k(0)= 0。q3( t)表示突加橫向白噪聲，q3( t) = g( t) · x( t)，x( t)表示零均值的隨機白噪聲，功率譜密度 S0= 106kg2/m2/s3為已知，g( t)為單位階躍函數。

采用虛擬激勵法[11]，求出方程（5）的解為：

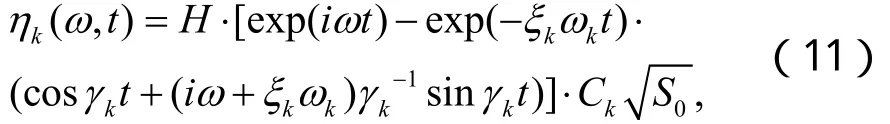
此時，模態坐標ηk( ω, t)的時變功率譜密度為：

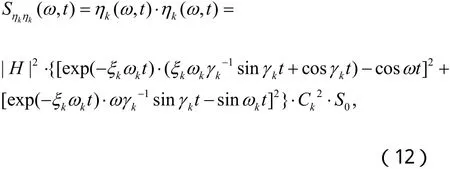
其中，等號右邊的上橫線表示取復數 ηk( ω, t)的共軛。

對上式在頻域上積分可得模態坐標 ηk(t)的時變方差為[11]：

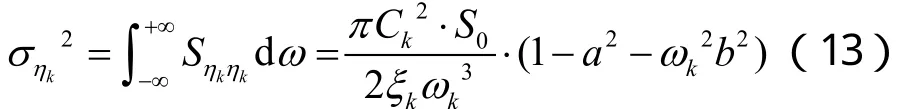
其中，

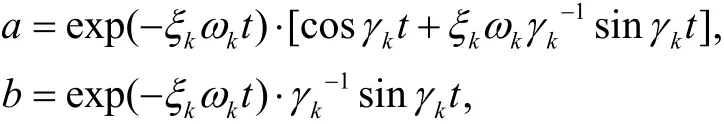
由方程（6），在只考慮軸對稱情況下（軸對稱時，不考慮環向坐標θ），可以推出：

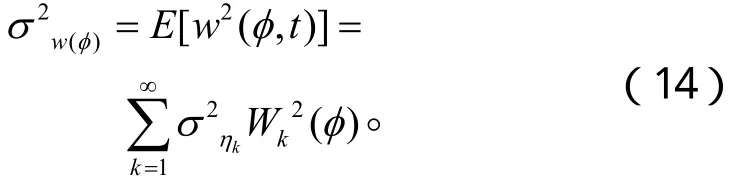
因此，如果知道了模態坐標的時變方差，結合振型函數，利用公式(14)，可以求出球殼任一點的均方響應隨時間的變化情況。球殼極點處在突加橫向均勻分布白噪聲激勵下均方響應的瞬態過程如圖3所示。

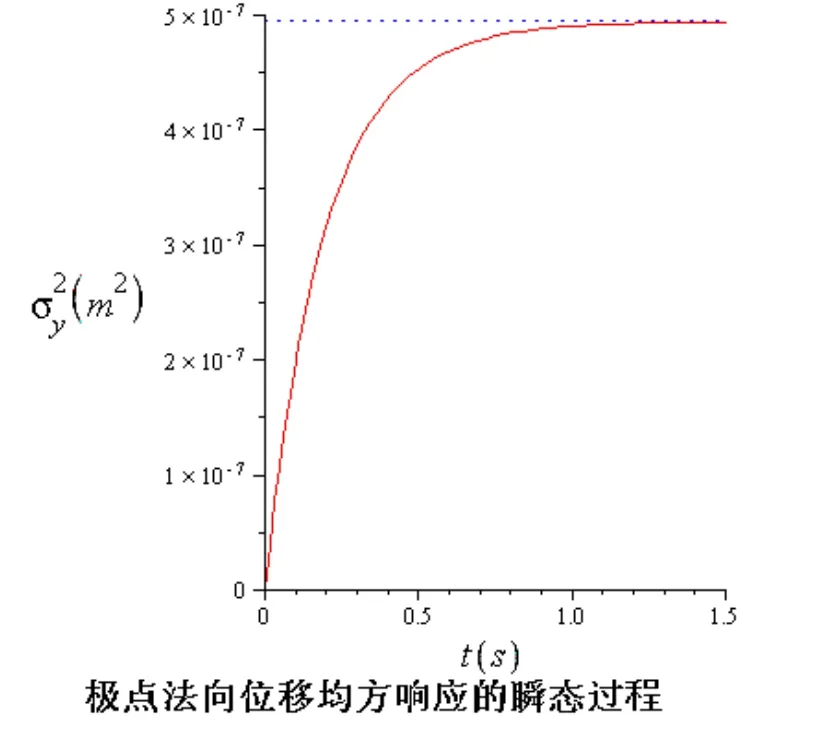
（圖3）

5 總結

本文借助經典薄殼理論，結合隨機響應問題的虛擬激勵方法，分析計算了橫向均勻分布的白噪聲激勵下周邊固支半球殼的均方響應。穩態響應的計算結果表明，殼體極點（中心對稱點）的均方響應為最大（見圖2）；而突加載荷作用時殼體極點處位移均方響應的時變方差曲線表明，由于系統中結構阻尼的存在，使得均方響應隨著時間的推移逐漸從下方趨向于穩態值。上述結果符合客觀實際，也佐證了本文所述方法適用于軸對稱情形下殼體的隨機響應分析。然而，如何將這類方法推廣到非軸對稱情形，尚有待進一步的研究。

[1] Kalnins A. Effect of bending on vibrations of spherical shells [J]. J Appl Mech, 1963, 36: 74-81.

[2] Kalnins A. Free vibration of rotationally symmetric shells [J]. The Journal of the Acoustical of America, 1964, 3(7): 1355-1365.

[3] Anand V Singh. Transient response of thin elastic spherical shells [J]. J Acoust Soc Am,1980, 68(1): 191-197.

[4] Singh A V. General vibration theory of deep spherical sandwich shells [D]. Canada: University of Ottawa, 1975.

[5] Kraus H, Kalnins A. Transient Vibration of Thin Elastic Shells [J]. J Acoust Soc Am, 1965, 38: 994-1002.

[6] Naghdi P M, Kalnins A. On vibrations of elastic spherical shells [J]. J Appl Mech, 1962, 29: 65-72.

[7] Kalnins A. Analysis of shells of revolution subjected to symmetric and nonsymmetric loads [J]. J Appl Mech, 1964, 31: 467-476.

[8] Werner Soedel. Vibrations of shells and plates [M]. New York: Marcel Dekker. 1981：199-226.

[9] 曹志遠. 振動理論[M]. 北京:中國鐵道出版社, 1989：327-343.

[10] 方同. 工程隨機振動[M]. 北京:國防工業出版社, 1995：69-116.

[11] 林家浩. 張亞輝. 隨機振動的虛擬激勵法[M]. 北京. 科學出版社, 2004：60-65.

[12] 孫慶鴻，張啟軍，姚慧珠. 振動與噪聲的阻尼控制[M]. 北京. 機械工業出版社, 1993：74-77.

[13] 尚新春. 密封容器組合殼自由振動的精確解[J]. 應用數學和力學，2001, 22(9)：934-942.

[14] 馬曉兵，尚新春，韓明芬. 柱殼和球殼振動的固有頻率計算及模態分析[J]. 工程力學，2002(增刊)：332-335.

[15] 黃克智，夏之熙，薛明德，等. 板殼理論[M].北京，清華大學出版社，1987：133-172.

[16] 紐蘭 D E. 隨機振動與譜分析概論[M]. 方同，黃嘉璜，朱位秋，譯.北京:機械工業出版社，1980：55-70.

[17] 胡海巖，孫久厚，陳懷海. 機械振動與沖擊（修訂版）[M]. 北京:航空工業出版社，1998：47-56.

Random Response Analysis of Semi-spherical Shell with Clamped Edge

LI Jun，LENG Xiao-lei
(Institute of Vibration Engineering Research, MOE Key Lab of Structural Mechanics and Control for Aircraft, Nanjing University of Aeronautics and Astronautics, Nanjing 210016, China)

Based on classical thin shell theory, intrinsic mode of a semi-spherical shell with clamped edge is analyzed by means of numerical calculation. Natural frequencies of free vibration under circumstances of axi-symmetry modes and natural modes of viberation expressed in terms of the Legendre functions are also calculated. Furthermore, based on the mode superposition method, response characteristics of horizontal excitation are presented. Finally, the mean square response of the shell excited by horizontal white noise is calculated in combination with the stochastic analysis theory, with transient/variable mean square response curves at each point of the shell presented.

spherical shell; stochastic vibration; mean square response

O383

A

1009－5160(2010)01－0035－04

*通訊作者：李軍（1970-），男，碩士，研究方向：板殼隨機振動研究.基金項目：國家自然科學基金資助項目（10672074）.