基于遺傳算法的支持向量機短期風速預測

周同旭

(皖西學院機械與電子工程學院,安徽六安 237012)

基于遺傳算法的支持向量機短期風速預測

周同旭

(皖西學院機械與電子工程學院,安徽六安 237012)

對風電場風速實現較準確的預測,可以有效減輕并網后風電場對電網的影響。支持向量機模型的預測精度在很大程度上依賴于模型參數的選擇,為提高預測模型的泛化能力和預測精度,應用遺傳算法選擇支持向量機的模型參數,再根據選擇的參數對小時風速進行預測。實驗結果表明本文方法能夠獲得較高的風速預測精度。

預測精度;支持向量機;遺傳算法;小時風速

1 引言

隨著我國能源結構的調整,可再生能源特別是風能的開發利用已得到高度重視,從技術成熟性和經濟可行性看,風電在可再生能源中具有很好的前景[1]。隨著風能的加速發展,越來越多的大型風電場納入統調電網,風電在電網的比重越來越大,同時風電的強隨機性增大了電力調度的難度。風速的準確預測有利于調度部門及時調整計劃,從而減輕風電對電網的影響[2]。

目前,風速預測常用的方法包括兩大類:傳統方法和現代方法。前者包括線性外推法、回歸分析法和時間序列法等。后者主要包括專家系統、支持向量機(SVM)[3]和人工神經網絡(ANN)[4-5]等。人工神經網絡一度成為預測領域的研究熱點,然而,人工神經網絡也有許多至今無法解決的問題。支持向量機是一種基于結構風險最小化原理的預測模型,其泛化能力要遠好于神經網絡和自回歸模型,近年來也被一些學者應用于風速預測。支持向量機模型參數對預測精度有很大影響[6],然而參數的確定還缺乏嚴格的數學方法。杜穎等人提出了用網格搜索法對SVM參數進行優化選擇[7]。郭輝等人提出基于三步搜索法的支持向量機參數優化方法[8]。這些方法都為支持向量機模型參數的優化選擇提供了有效的途徑。

遺傳算法(GA)能使種群達到全局最優收斂。與傳統算法相比,遺傳算法無需先驗知識,而且對初始參數不敏感,所以不會陷入局部極小點。本文利用遺傳算法對支持向量機模型參數進行優化選擇(GA-SVM),并用參數優化后的支持向量機模型對某風電場的小時平均風速進行預測,取得了較高的預測精度。

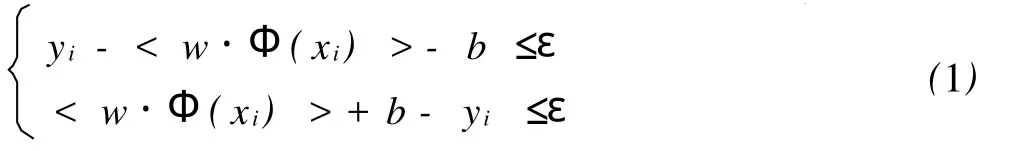
2 支持向量機

支持向量機應用于回歸方面,主要有Vapnik提出的ε-回歸支持向量機(ε-SVR)。設有回歸函數f(x)=+b用于擬合樣本數據,假設所有訓練樣本在給定精度ε下用該函數擬合,即

式中,i=1,2,…,k。

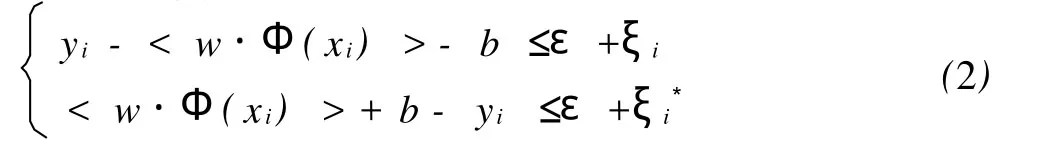
優化目標為:

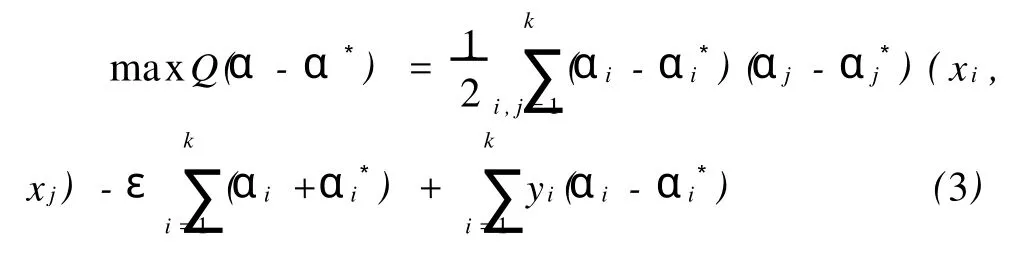
約束條件為

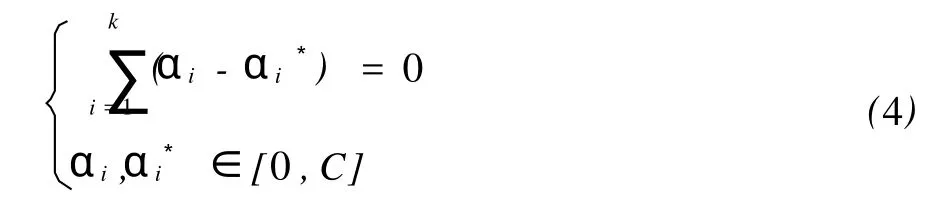
求解上述問題并引進核函數 K(x,x′)后,得到w和待估計函數

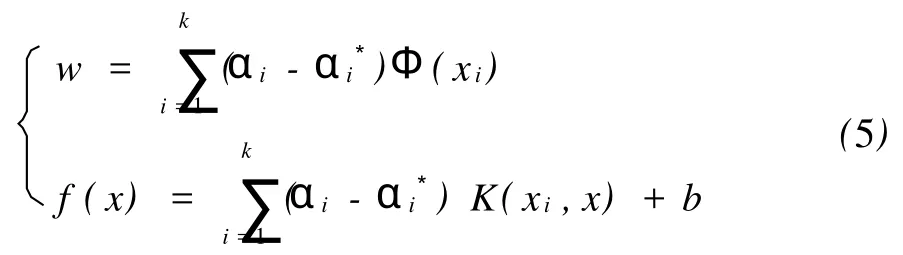
其中(αi-α＊i)≠0對應的 xi即為支持向量。

在SVM模型中通過對上述三種核函數的比較,發現徑向基核函數性能最好,本文也將采用徑向基核函數。其表達式為:

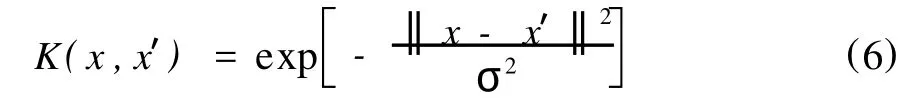
3 遺傳算法

支持向量機模型參數ε、C和核函數參數σ2的選擇對精度影響很大,目前還缺乏嚴格的數學計算方法,這三個參數的組合本質上是一種優化過程。本文將遺傳算法應用于參數ε、C和核函數參數σ2的優化中,適應度函數采用均方根誤差的倒數。

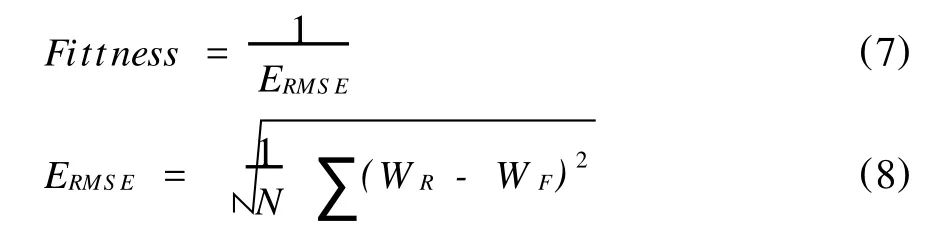
其中,N為樣本個數,WR為實測值,WF為預測值。算法步驟如下:

Step1編碼:將解空間的數據ε、C和σ2表示成遺傳空間的基因型數據,這些基因型數據的不同組合就構成了不同的點。本文采用二進制編碼法。

Step2初始化種群:隨機產生 N個初始基因型數據,每個基因型數據稱為一個個體,N個個體構成一個群體。GA以這個N字符串為初始點開始迭代。

Step3個體適應度計算:計算個體適應度,并判斷是否符合優化準則,若符合,輸出最佳個體及其代表的最優解,并結束計算,否則轉向Step4。

Step4選擇:根據每個個體的適應度值,選擇一些優良的個體遺傳到下一代群體中。適應性強的個體被選中的概率高,適應度低的個體可能被淘汰。

Step5交叉:將群體內的各個個體隨機搭配成對,對每一個體以某個概率(稱為交叉概率)交換它們之間的部分染色體。

Step6變異:對群體中的每一個個體,以變異概率改變某一個或某一些基因座上的基因值為其他的等位基因。

Step7判斷運算:判斷新一代群體是否滿足結束條件,如果滿足,則停止;不滿足,則轉至Step3步驟繼續進行計算。

4 風速時間序列GA-SVM預測

仿真試驗數據來源為我國某風電場2004年6月1日至6月15日共360小時平均風速數據,實驗在CPU主頻為2.4GHz、內存為2.0GB的PC機上進行,仿真軟件為MATLAB7.4。

4.1 樣本構造

風速數據是一組隨時間變化的數據序列,記為{xt,t=1,2,…,n},支持向量機在選擇輸入輸出變量前需對數據序列進行相空間重構,即把時間序列組轉化為矩陣形式來尋找數據間的關系。將原數據序列進行相空間重構,構造樣本對(Xt,Yt),其中 Xt= {xt-m,xt-m+1,…,xt-1},Yt=xt,m為輸入向量的維數,xi為第i個樣本。m的確定一般采用以均方根誤差最小化為原則的增長法,即令 m從1開始逐漸增加,比較每次的驗證誤差,取誤差最小時的m值作為輸入維數。通過計算風速時間序列自相關系數可以確定輸入維數。本算例風速序列的自相關系數曲線如圖1所示。

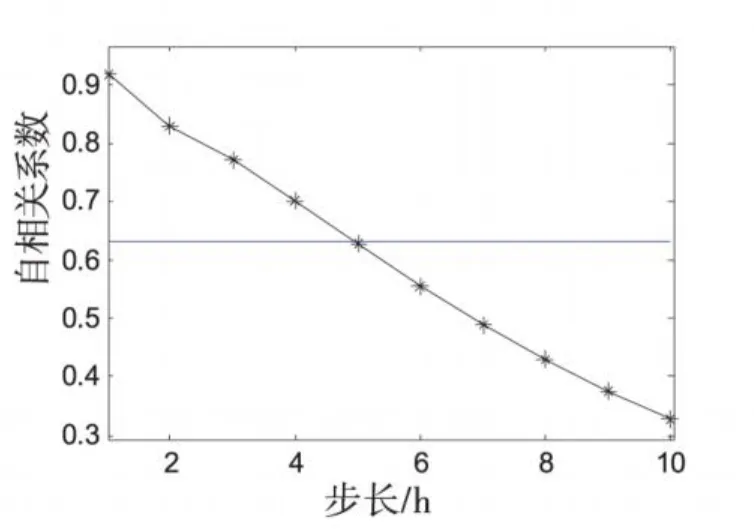
圖1 風速序列自相關系數

取當自相關系數降至1-e-1時的延時步長5做為輸入樣本的維數m,即用前5天的風速預測第6天的風速。按照輸入樣本的維數,從原始數據中構造200個訓練樣本對和50個測試樣本對。

4.2 歸一化處理

對支持向量機預測模型的輸入變量采用如下規范化的方法進行預處理。設風速序列最大值為 vmax,最小值為vmin,某一個風速v的規范化變量定義為:

這樣每個輸入變量的取值范圍都在0～1之間,皆是具有相同尺度的無量綱量。

4.3 參數尋優

利用上述遺傳算法的步驟對SVM的參數ε、C和σ2的最佳組合進行優化,采用二進制編碼方法,設置種群規模為100,每個個體由代表三個參數的三個基因組成,每個基因長度均為40位,所以每個個體碼串長度為120位,進化代數最大值設為200,交叉概率0.8,變異概率為0.1。最后得到參數最優化組合為:

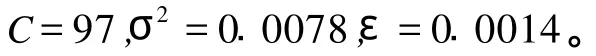
4.4 支持向量機建模

根據樣本集建立如式(3)所示的目標函數,并用序列極小化訓練算法求解,得到解 ai和a＊i,i=1,2,…,k;將得到的拉格朗日乘子代入式(5)中,再利用預測樣本對未來某一點風速進行預測。

4.5 SVM訓練與預測

采用數據滾動方法對模型進行訓練和預測,以進行后1h的風速預測。依此類推完成全部的風速預測,這樣使網絡能夠反應風速最新變化規律。采用絕對百分比誤差(APE)、平均絕對百分比誤差(MAPE)對預測效果進行評價。

為了說明支持向量機在預測方面的性能以及遺傳算法在SVM參數尋優方面的有效性,本文將GA-SVM法、文獻[7]提出的SVM網格搜索參數法(GRID-SVM)以及BP神經網絡法分別應用于風速預測。這里的BP神經網絡層數確定為3層,學習和測試樣本與SVM相同,輸入層節點數為5,輸出層節點數為1,隱含層節點通過實驗比較取12個。神經網絡第一層與第三層選用線性傳遞函數,第二層選用對數S型傳遞函數,利用L-M法進行訓練。圖2(a)、(b)、(C)分別是BP、GA-SVM和GRID-SVM三種方法的預測曲線。表1為三者預測結果。從圖2的預測曲線和表1的數據可以看出:

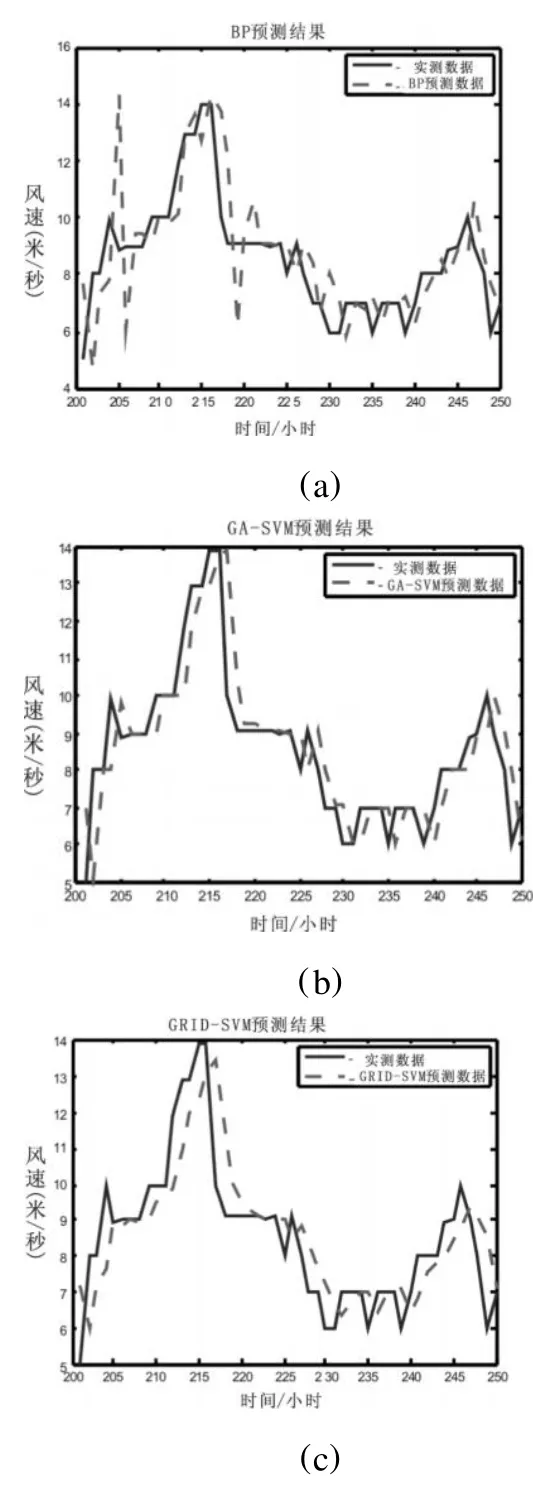
圖2 預測曲線

(1)BP預測方法總體預測效果并不理想,其 MAPE達到15.2%。顯然基于支持向量機的兩種方法GA-SVM和GRID-SVM的預測效果均好于BP神經網絡,這是因為SVM模型基于結構風險最小化原則,得到的是全局最優解,其泛化性能高于BP神經網絡。

(2)在訓練時間方面,雖然SVM方法訓練和預測時間比BP要快得多,但參數尋優耗時較多,所以從表1看出,GA-SVM和GRID-SVM兩種方法的總耗時均多于BP網絡,GA-SVM較GRID-SVM耗時要少。

(3)通過試驗發現,GA-SVM法比 GRIDSVM法具有更高的預測精度,兩者的MAPE分別為9.7%和10.6%。

為進一步實驗驗證該算法,本文將 GA-SVM網絡與RBF、BP網絡同時對美國加州某風電場的兩個測風站的風速進行預測。RBF網絡采用從樣本中選擇固定隱層中心的方法,隱層神經元使用相同寬度,輸出層權值使用最小二乘法求解。BP隱層函數選擇高斯函數。GA-SVM采用前文使用的網絡結構及算法。通過實驗得到如表2所示的結果。

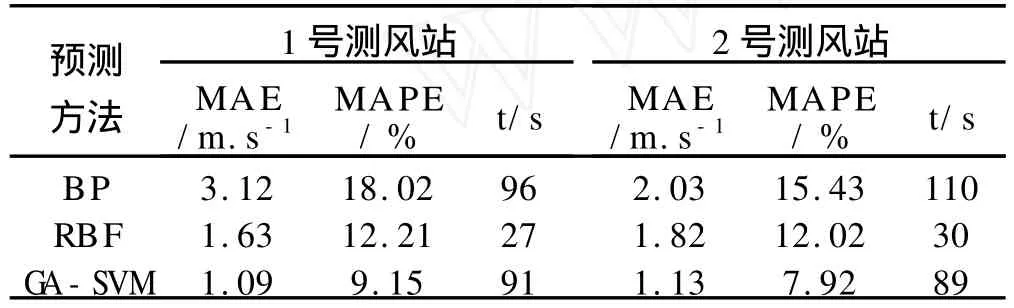
表2 三種方法預測結果

結果表明在這三種網絡模型中,GA-SVM網絡具有最好的學習、映射和泛化能力,其絕對百分比誤差和平均絕對誤差比BP、RBF網絡都小。

5 結束語

本文提出了一種結合了遺傳算法的支持向量機風速預測模型。支持向量機基于結構風險最小化,具有優越的泛化性能,得到的是全局最優解,解決了采用神經網絡方法時無法避免的局部極值問題;通過遺傳算法對支持向量機模型參數進行優化選擇,保證了較高的預測精度。仿真表明 GA-SVM法相對于GRID-SVM和BP神經網絡法具有更高的預測精度及更強的魯棒性,預測風速的MAPE在10%以內,達到很好的效果。

[1]Alexiadis M,Dokopoulos P,Sahsamanoglou Het al.Short Term Forecasting of Wind Speed and Related Electrical Power[J].Solar Energy,1998,63(1):61-68.

[2]潘迪夫,劉輝,李燕飛.風電場風速短期多步預測改進算法[J].中國電機工程學報,2008,28(26):87-91

[3]王慧勤.基于支持向量機的短期風速預測研究[J].寶雞文理學院學報(自然科學版),2009,29(1):16-18.

[4]Kariniotakis G,Stavrakakis G,Nogaret E.Wind Power Forecasting Using Advanced Neural Network Models[J].IEEE Trans.on Energy Conversion,1996,11(4):762-767.

[5]Li Shuhui,Wunsch D C,Giesselmann M G,et al.Using Neural Networks to Estimate Wind Turbine Power Generation[J]. IEEE Trans.on Energy Conversion,2001,16(3):276-282.

[6]Ping-Feng Pai,Wei-Chiang Hong,and Yu-Shen Lee1. Determining Parameters of Support Vector Machines by Genetic Algorithms-Applications to Reliability Prediction [J].International Journal of Operations Research,2005,2 (1):1-7.

[7]杜穎,盧繼平,李青,等.基于最小二乘支持向量機的風電場短期風速預測[J].電網技術,2008,32(15):62-66.

[8]郭輝,劉賀平,王玲.最小二乘支持向量機參數選擇方法及其應用研究[J].系統仿真學報,2006,18(7):2033-2051.

Forecasting of Short-term Wind Speed with Support Vector Machine Based on Genetic Algorithms

ZHOU Tong-xu
(College of Mechanical and Electrical Engineering,West Anhui University,L u’an237012,China)

Giving a high precise wind speed forecast for wind farms can effectively relieve disadvantageous impact of wind power plants on power systems.The selection of parameters for Support Vector Machine(SVM)has a large impact on the forecasting accuracy.For enhancing the generalization performance and prediction accuracy,genetic algorithms(GA)are applied to select parameters for SVM model in this study,and then hourly wind speed are forecasted according the selected parameters.The simulation results show that using the model proposed on the paper to predict wind speed can achieve a high accuracy.

forecasting accuracy;support vector machines;genetic algorithms;hourly wind speed

O441.1

A

1009-9735(2010)05-0106-04

2010-08-07

皖西學院自然科學應用研究項目(WXZY0704)。

周同旭(1975-),男,安徽六安人,講師,碩士,研究方向:檢測技術,電力電子技術。