具有年齡結構的SI傳染病模型的分析

張 劍，張宏民

（齊齊哈爾大學理學院，黑龍江 齊齊哈爾 161006）

近幾年來，隨著SARS，甲型H1N1等眾多新型傳染病的出現，使得人們對于傳染病的研究又加以關注。傳染病的防治是關系到人類健康和國計民生的重大問題，對疾病流行規律的定量研究是防治工作的重要依據，根據疾病的發生、發展及環境變化等情況，建立能反映其變化規律的數學模型，通過模型動力學性態的研究來顯示疾病的發展過程，預測其流行規律和發展趨勢，分析疾病流行的原因和關鍵因素，尋求對其進行預防和控制的最優策略，為人們防治決策提供理論基礎和數量依據。由此可見，研究種群的傳染病模型對于種群的生存與發展是至關重要的。眾多研究考慮了疾病在食餌之間傳播的模型，得到疾病流行的閾值條件[1]。分析了捕食者具有疾病的SI模型，討論了解有界性和平衡點全局穩定性[2]。并分別對具有年齡結構的SEIR和SIS傳染病模型進行了分析[3-4]。但對具有年齡結構的單種群模型，在成年種群染病的SI問題尚未討論過。本文根據成年和幼年種群不同的生長特性，以及疾病對不同年齡結構的兩種群的影響，發展規律和傳播特性等因素研究該類模型，進而可以顯示疾病的發展過程，揭示其流行規律，為人們防治決策提供理論基礎。

1 模型的建立與假設

具有年齡結構的傳染病模型如下：

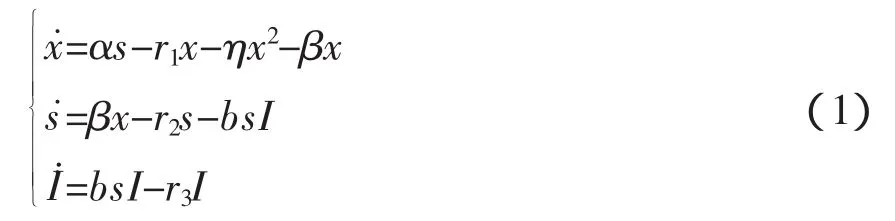
其中，x表示幼年種群數量；s表示易感的成年種群數量；I表示染病的成年種群數量；α表示幼年種群的出生率；r1、r2、r3分別表示幼年種群、易感的成年種群、染病的成年種群的死亡率；η表示幼年種群的密度制約系數；β表示幼年種群向成年種群的轉化率；b表示接觸率。

根據模型的生態意義，本文在

R3+=上討論。

根據模型的實際背景作如下假設：①假設疾病只在成年種群間傳播。②不考慮種群的流動性。③成年種群患病后不能夠治愈；患病后一旦與易感染者接觸即具有一定的傳染率。

2 模型平衡點的存在性

定理1模型（1）的平衡點存在的條件：

證明：模型（1）的平衡點是滿足下面方程組的解。

根據方程組（2）可知模型（1）存在三個平衡點分別是E0（0，0，0），E1（x0，s0，0）和唯一的正平衡點E2（x*，s*，I*）。

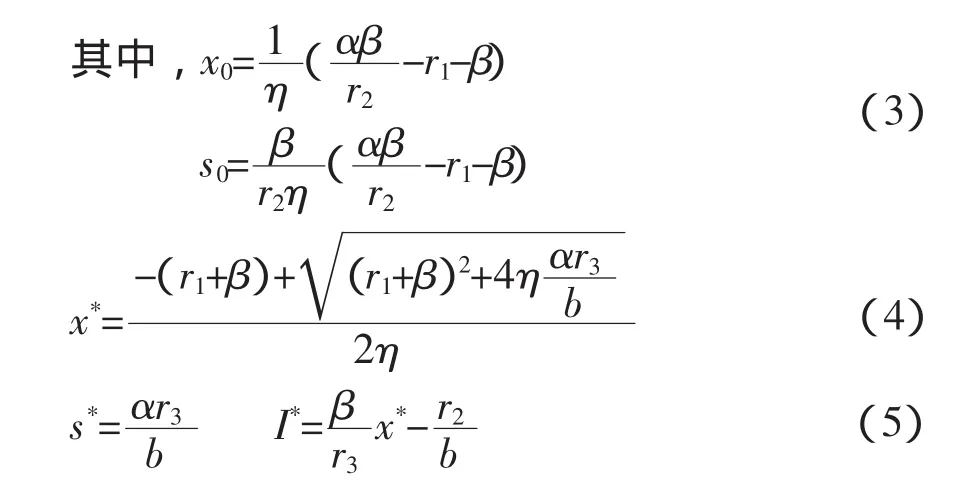
根據模型的實際生態意義知（3），（4），（5）各式應恒大于0，因此得到模型（1）的平衡點存在的條件是：

3 平衡點的穩定性

定理2當αβ-r2（r1+β）＜0時，模型（1）的平衡點E0是局部漸近穩定的；當αβ-r2（r1+β）＞0時，平衡點E1是局部漸近穩定的。

證明：模型（1）的Jacobi系數矩陣為

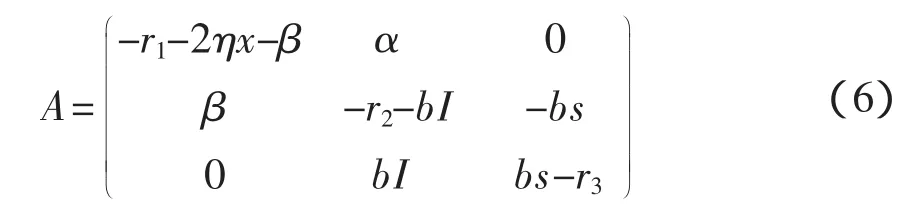
下面分別平衡點E0和E1的穩定性進行討論。

平衡點E0（0，0，0）的系數矩陣是

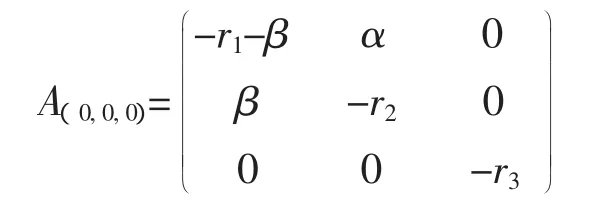
而其對應的特征方程是

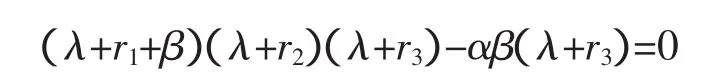
特征根是 λ1=-r3＜0

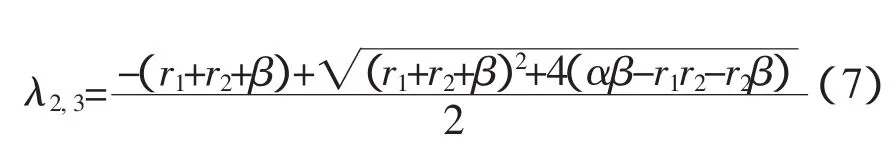
平衡點E1（x0，s0，0）的系數矩陣是

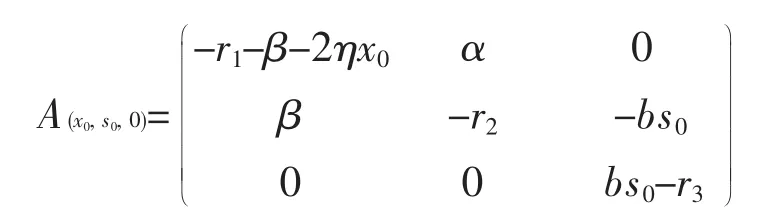
而其對應的特征方程是

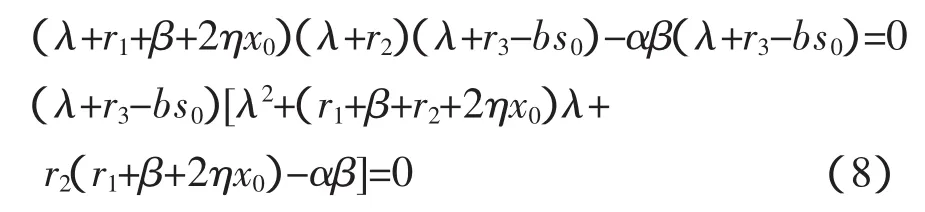
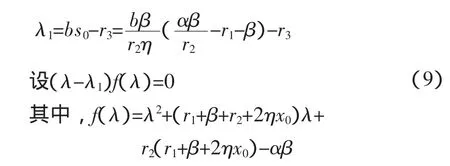
f（0）=αβ-r2（r1＋β）＞0（由E1的存在性知）則λ2，λ3是兩個具有負實部的特征根。

證明：E2（x*，s*，I*）的系數矩陣是

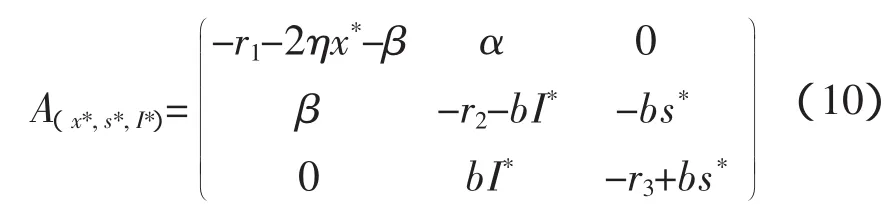
特征方程為 λ3+A1λ2+A2λ+A3=0

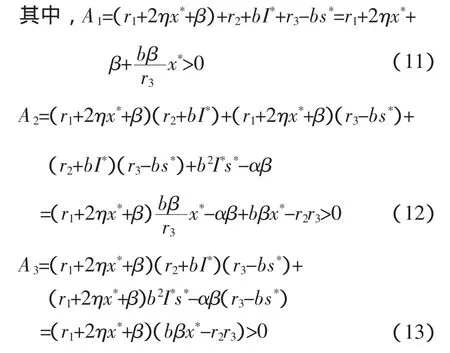
由 E2的存在性知 A1＞0，A2＞0，A3＞0。

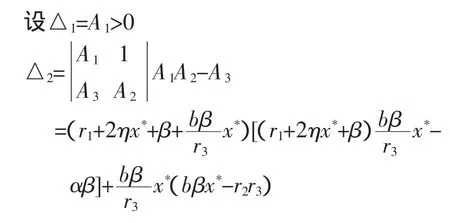
由 E2存在，知 bβx*-r2r3＞0

由 A2＞0 知

△3=A3△2＞0。

根據Hurwitz判別法知，點E2對應的特征方程所有特征根均有負實部，故平衡點E2局部漸近穩定。因此只要正平衡點E2存在，其必定是局部漸近穩定的平衡點。

4 模型試驗驗證

5 結 論

本文所研究的具有年齡結構的SI傳染病模型，是將生物個體按其生理年齡進行分類，以便更好地反映個體的生理特征和影響疾病傳播方面的差異，在疾病在成年種群間傳播的假設條件下，得到平衡點的局部穩定性。，E2是局部漸近穩定的。說明此時，模型的唯一正平衡點存在且局部穩定，也就是說疾病不會造成兩個年齡結構的種群的滅絕。該模型可以用來解釋在假設條件下的生物種群在疾病的發生及種群內的傳播等因素，通過對模型動力學性態的定性、定量分析，能夠揭示其發展變化趨勢，分析疾病流行的原因和關鍵因素，尋求對其預防和控制的最優策略。人們可以利用該結論，創造良好的環境，使得疾病在生物種群中不造成較大的影響，不會造成種群的滅絕。這類模型在描述與年齡有關的疾病的傳播規律時將更加有效和實用。本文的研究結果，對于生物部門控制疾病在生物種群間的傳播具有一定的參考價值。

[1]Chattopad J,Arino O.A predator-prey model with disease in the prey[J].Nonlinear Anal,1999,36∶749-766

[2]張江山,孫樹林.捕食者有病的生態流行病模型的分析[J].生物數學學報,2005,20(2)∶157-164.

[3]王定江.時變年齡結構的SEIR傳染病模型解的存在性[J].數學的實踐與認識,2003,33(8)∶91-96.

[4]EI-Doma M.Analysis of an age-dependent SIS epidemic model with vertical transmission and proportionate mixing assumption[J].Math Comput Model,1999,29∶31-43.

[5]王靜,王克.具有年齡結構的單種群模型單一捕獲的優化問題[J].東北師范大報∶自然科學版,2003,35(2)∶1-6.

[6]陳蘭蓀.數學生態學模型與研究方法[M].北京∶科學出版社,1988∶156-172.

[7]Li Y F,Wang W.Characteristics of monoclonal antibody against infectious bursal disease virus[J].Journal of Northeast Agricultural University∶English Edition,1999,6(2)∶128-132.

[8]張劍,張宏民,丁麗英.捕食-食餌系統的捕獲優化問題[J].東北農業大學學報,2007,38(3)∶384-386.

[9]李益群,任謹慎,李建全.一類帶有一般出生率的SIS傳染病模型的全局分析[J].數學的實踐與認識,2009,39(23)∶176-181.

[10]陳庚.一類具有年齡結構的傳染病模型的持續性質[J].高校應用數學學報∶A 輯,2007,22(3)∶253-262.

[11]何澤榮,雒志學.一類帶接種和年齡結構的流行病模型分析一類帶接種和年齡結構的流行病模型分析[J].工程數學學報,2003,20(2)∶41-45.

[12]王曉燕,楊俊元.具有Logistic增長和年齡結構的SIS模型[J].數學的實踐與認識,2007,37(15)∶99-103.

[13]田燦榮.一類具常數接觸率傳染病模型的穩定性分析[J].生物數學學報,2009,24(1)∶47-56.

[14]Allen L J S,Burgin A M.Comparison of deterministic and stochastic SIS and SIR models in discrete time[J].Mathematical Biosciences,2000,163∶1-33.

[15]DiekmannO,Gyllenberg M.On the formulati on and analysis of general deterministic structured population modelsⅡ.Nonlinear theory[J].Math Biology,2001,43(2)∶157-189.