基于改進閾值消噪算法的小波包降噪

于文新， 張 謙

（①湖南中移鼎訊通信有限公司,湖南 長沙 410011; ②長沙理工大學 數(shù)學與計算科學學院,湖南 長沙 410011）

0 引言

在實際的應用中，信號和噪聲總是同時出現(xiàn)的，信號在形成、傳輸過程中，常因外界噪聲干擾而導致其質(zhì)量退化，如何更好地保護信號和抑制噪聲一直是信號處理的熱點[1-2]。小波閾值去噪根據(jù)噪聲通常表現(xiàn)為高頻信號的特性，對小波分解的高頻系數(shù)進行門限閾值處理，達到去噪的目的。

小波包分解是小波分析的進一步推廣，它對小波分析沒有細分的高頻進一步分解，因此可以將高頻噪聲和高頻信號區(qū)分開來，從而獲得更為理想的去噪效果。由于通常采用的硬閾值函數(shù)的不連續(xù)性，以及軟閾值函數(shù)中估計小波系數(shù)與帶噪信號的小波系數(shù)之間存在著恒定的偏差的缺陷, 本文提出了一種基于小波包的新閾值函數(shù),并用Matlab仿真實驗表明了該方法的優(yōu)越性。

1 小波包消噪原理

不論是多分辨分析還是小波包分析，其分解的最終目的是力求構造一個在頻率上高度逼近Hilbert空間2()LR的正交小波基（或正交小波包基）。

但隨著尺度j的增大，相應的正交小波基函數(shù)的空間分辨率越高，而其頻率分辨率越低，這正是正交小波基的一大缺陷。而小波包卻具有將隨j增大而變寬的頻譜窗口進一步分割變細的優(yōu)良性質(zhì)，從而克服了正交小波變換的這一不足。在小波包標架中，其信號消噪的算法思想與在小波標架中的基本一樣，只是小波包分析對上一層的低頻部分和高頻部分同時進行了細分。在閾值量化過程中，其方法與小波分析一樣。

1.1 小波包算法

1.2 無偏估計

其中：分別為小波系數(shù)和其估計值。

本文引入一個關于觀測值S的函數(shù)：

其中：

SURE為上述風險函數(shù)的無偏估計，表達式為：

2 閾值消噪原理

閾值的選取主要由小波變換的方法、小波函數(shù)的性質(zhì)以及信號和噪聲的性質(zhì)等因素所決定，閾值規(guī)則的選取有很多種。常見的閾值選擇分硬閾值和軟閾值[3-5]兩種處理方式。軟閾值處理即把信號的絕對值與閾值進行比較,當數(shù)據(jù)的絕對值小于或等于閾值時,令其為零,大于閾值的數(shù)據(jù)點則向零收縮,變?yōu)樵擖c值與閾值之差;對于硬閾值處理,是把信號的絕對值與閾值進行比較,小于或等于閾值的點變?yōu)榱?大于閾值的點不變。

2.1 改進閾值函數(shù)及迭代運算的實現(xiàn)

本文采取類Sigmoid函數(shù)作為改進的軟閾值函數(shù)[6-9]。相對其他改進的閾值函數(shù)，類Sigmoid函數(shù)二階可導，而且由于類Sigmoid函數(shù)本身對漸近線的快速逼近性，當大于所取閾值時，根據(jù)類Sigmoid函數(shù)選取的小波系數(shù)保持與標準軟閾值收縮后的小波系數(shù)更近的相似性。

類Sigmoid函數(shù)所確定的閾值函數(shù)為[7]：

式中：x為小波系數(shù)，式（4）中，當k=∞時，式（6）為標準軟閥值函數(shù)。在閥值函數(shù)式（6）的條件下，由此可得:

若采用正交小波，由式（2）把均方差分解到各尺度的小波系數(shù)中去，在針對每一尺度的小波系數(shù)及其估計值進行迭代運算，運算式為：

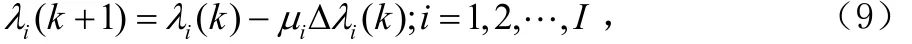
2.2 小波包消噪處理步驟

信號消噪是小波包分析的一個最基本的應用，通常,它按照如下幾個步驟進行：

①信號的小波包分解。選擇一個小波并確定一個小波分解的層次N ,然后對信號S 進行N 層小波包分解;

②計算最佳樹（即確定最佳小波包基）。對于一個給定的嫡標準計算最佳樹。對于 GUI 方式,有一個專門的“Best Tree”按鈕用于計算最佳樹;

③小波包分解系數(shù)的閾值量化。利用式（6）的閥值函數(shù)對小波系數(shù)進行處理，得到各尺度小波系數(shù)的估計值，然后根據(jù)利用式（10）得到：

④小波包重構。根據(jù)小波分解的第 N 層的低頻系數(shù)和經(jīng)過量化處理后的從1 到N 層的高頻系數(shù),進行小波重構。

由于對于一個給定的正交小波，一個長度為 2LN= 的信號最多可以有2L種不同的分解方式，這恰好是一個深度為L的完整二叉樹的二叉子樹的數(shù)目，是一個非常龐大的數(shù)目。因此，步驟②得出的最佳分解方式，只對最佳樹選中的高頻系數(shù)進行下一層分解。在這4個步驟之中,最關鍵的就是如何選取閾值和如何進行閾值的量化。從某種程度上說,它直接關系到信號消噪的質(zhì)量。

3 Matlab實驗結果及分析

為了說明新閾值函數(shù)的有效性和優(yōu)越性，對某一含噪信號分 別應用經(jīng)典的軟硬閾值函數(shù)和新閾值函數(shù)對信號進行小波包降噪處理。將原始信號作為標準信號s(n)，含噪信號為f(n），信號長度為L，信噪比（RSN）公式定義為：

原始信號與估計信號之間的均方根誤差(RMSE)定義為：

仿真結果如圖1所示。

圖1 各種閾值函數(shù)降噪結果的比較

降噪信號的信噪比(SNR)和均方誤差（RMSE）如表1所示。研究表明，新閾值函數(shù)的小波包信號降噪在均方根誤差（RMSE）和信噪比（SNR）兩個性能指標上均優(yōu)于經(jīng)典的軟硬閾值函數(shù)。

表1 各種方法的均方誤差(RMSE)和信噪比(RSN)(dB)

4 結語

信號的信噪比SNR越高，原始信號與估計信號的均方根誤差RMSE越小，則估計信號就越接近于原始信號，消噪效果越好。本文在經(jīng)典的小波軟、硬閾值消噪方法的基礎上提出了一種基于小波包分析的改進方法即基于改進閾值消噪算法的小波包降噪方法。通過Matlab仿真實驗結果表明，本文采用小波包的改進閾值法克服了軟、硬閾值方法的缺點，更好地保護了信號并且抑制了噪聲，同時，應用此消噪方法的效果比小波消噪方法要好。因而具有一定的工程意義和應用價值。

[1] 尹劍侖,衛(wèi)武迪.一種改進的自適應中值濾波算法研究[J].通信技術,2009,42(11):241-243.

[2] 劉芬,楊濟安.基于小波變換的遙感圖像無損壓縮算法研究[J].通信技術,2007,40(07):6-8.

[3] Donoho D L, Johnstone I M. Ideal Spatial A Daptation Via Wavelet Shrinkage[J].Biometrika,1994,81(12):425-455.

[4] Donoho D L.De-noising by Soft-thresholding[J].IEEE Trans on IT,1995,41(03):613-627.

[5] Donoho D L,Johnstone I M.Adapting to Unknown Smoothness Via Wavelet Shrinkage[J].Journal of American Stat Assoc,1995,12(90):1200-1224.

[6] 劉守山,楊辰龍.基于自適應小波閥值的超聲信消噪[J].浙江大學學報:工學版,2007(09):1557-1560.

[7] Zhang X P, Desal M D. Adaptive Denoising Based on SURE Risk[J].IEEE Signal Processing Letters,1998,5(10):265-267.

[8] 曲天書, 戴逸松, 王樹勛. 基于SURE無偏估計的自適應小波閥值去噪[J].電子學報,2002,30(02):266-268.

[9] 程正軍,張運陶.基于MATLAB的小波包分析在信號降噪中的應用[J].西華師范大學學報:自然科學版,2004(03):48-54.