基于遺傳算法的固定費用運輸問題研究

吳開信，牟瑞芳

（1.西南交通大學 交通運輸學院，四川 成都 610031；2.華僑大學 廈門工學院，福建 廈門 361021）

運輸問題是線性規劃的重要分支，很多實際問題可以轉化為運輸模型來求解。簡單的線性運輸模型僅考慮兩組約束條件：即與源節點相關的m個約束條件和與目的節點相關的n個約束條件。固定費用運輸問題(FCTP)是運輸問題的擴展，它除了要考慮兩組約束條件以外，還要考慮每次運輸時的固定成本和與運量有關的可變成本，簡單的線性運輸問題可以看作所有路徑的固定成本為零的FCTP問題。簡單線性運輸問題的解法通常是用表上作業法，對于源節點和目的節點較多的運輸問題，表上作業法計算量較大、效率低，而基于遺傳算法運輸問題的求解將更具有實效性。

由于FCTP問題的目標函數具有不連續性，所以比簡單的線性運輸問題更難處理，Hirsch和Dantzig證明了其最優解一般在問題約束條件構成的凸集的某個極值點上[1]。在早期的研究中，一些精確解法被運用于求解FCTP問題，如極點排列法和分支定界法等[2]。但這些算法沒有充分利用固定費用運輸問題的網絡特征，只適合于解決規模較小的此類問題。后來一些啟發式算法，如拉格朗日松弛法、模擬退火算法等被引入解決FCTP問題，但在實際運用中發現這些算法獲得的解質量較差。本文根據FCTP問題的最優解是一個生成樹的網絡特性，結合遺傳算法設計出一種基于運輸樹的遺傳算法，并給出實例得出運用此方法可以快速提高獲得最優解的幾率。

1 問題的描述

對于FCTP問題，可用以下數學模型表示：

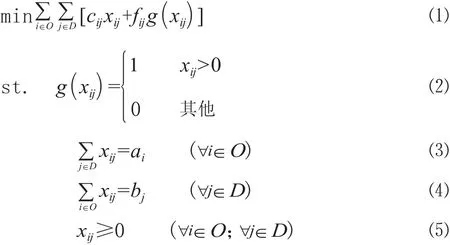
式中：O和D分別表示m個源節點的集合和n個目的節點的集合；cij、fij和xij分別表示源節點i到目的節點j的單位可變成本、總的固定成本和運輸數量；條件⑶和條件⑷分別表示產銷平衡條件下物資總的供應量和總的需求量，如果是產銷不平衡運輸問題，可以通過增加一個虛擬產地或虛擬銷地轉化為產銷平衡的運輸問題；目標函數表示求總運輸成本最小的分配方案[3]。

運輸問題可用一個網絡二分圖來表示，因此可以嘗試運用基于運輸生成樹的遺傳算法來進行求解。假設某運輸問題有m個源節點和n個目的節點，則FCTP問題的運輸網絡圖具有以下3個特點：①由于約束方程最多有m+n-1個獨立方程，即系數矩陣的秩小于等于m+n-1，因此共有m+n-1個基變量，每個變量對應運輸表中的1格；②基變量一定能構成1棵運輸樹，即在運輸表中的每一行和每一列中至少存在1個基變量；③基變量不能構成閉合回路。

2 基于運輸樹的遺傳算法

2.1 編碼

設集合O表示m個源節點的集合，O={1,2,…,m}，集合D表示n個目的節點的集合，D={m+1,m+2,…,m+n}，則運輸網絡圖中有m+n個節點和mn條邊。

運輸問題有特殊的數據結構，由圖論知識可知，對于1個含m+n個節點的完備圖，可以表示(m+n)m+n-2棵標號不同的樹，也就是說，我們可以用m+n-2個數字的排列表示m+n個節點的樹，其中任何樹至少有2片葉子[4]。

在{1,2,…,m+n}共m+n個數字中隨機可重復地選取m+n-2個數字按順序排成1排，構成1個初始染色體，染色體中的基因可以相同。運輸樹和染色體之間的轉換關系按下列法則。

2.1.1 運輸樹轉換成染色體

步驟1：令i是樹中最小的葉子節點，j為i的關聯節點，選擇j為染色體中最右邊的數字，再刪除節點i和邊(i,j)；

步驟2：重復上一步m+n-2次，直至剩下2個節點為止，此時染色體生成。

2.1.2 染色體轉換成運輸樹

設P為一個染色體，S為{1,2,…,m+n}中沒有在P里出現的所有數字構成的集合。設i是S中最小的數字，j是P中最左邊的數字，重復以下步驟，直至P中沒有數字為止。

步驟1：若i∈O和j∈D，則(i,j)構成運輸樹的1條邊，否則選擇j后面與i不在同一個集合中的元素k，交換 j 和 k 的位置，此時(i,k)構成運輸樹的1條邊。

步驟2：從S中去掉元素i，若P中仍含有與j相同的元素，則從P中直接去掉元素j即可；否則從P中直接去掉元素 j 后，在S中增加元素j。

步驟3：若P中沒有元素了，則S中剩下的最后兩個元素構成運輸樹的第m+n-1條邊。

步驟4：分配運行量x?=

步驟5：更新產量ai=ai-xij和銷量bj=bj-xij。

步驟6：若沒有可行的運量分配，則停止；否則，去掉運量為0的邊，對產地r和銷地s增加邊(r,s)，且xij=ar=bs。

運輸樹總可以按上面的法則轉換為染色體，反之不然，只有可行的染色體才能通過上面的法則轉換成運輸樹。由于初始染色體是從{1，2，…，m+n}中隨機可重復地選取m+n-2個數字產生，未必是可行染色體，即初始染色體未必能生成1棵運輸樹，在此必須根據運輸樹特殊的數據結構制定可行性準則，對初始染色體進行篩選。

由運輸樹圖形可知，染色體中出現次數為t的基因(節點)與其他節點有t+1個連接，由此對初始染色體可制定以下可行性準則：，其中Lo和LD分別表示染色體中含集合O基因的連接數和含集合D基因的連接數，分別表示集合S中含集合O基因的個數和含集合D基因的個數。

可行性初始染色體可以編制計算機程序在java環境下執行生成。

2.2 適應函數

適應度是1個群體中個體生存機會選擇的惟一確定性指標，適應度較高的個體遺傳到下一代的概率較大。適應函數可表示為：

2.3 選擇策略

采用最優方式實現選擇操作，即在父代種群中適應度最大的染色體在子代中至少出現1次，然后按照輪盤賭選擇的方式進行選擇操作，以保證優良的染色體進入到下一代。

2.4 單點交叉操作

在父代A和父代B中作如下交叉操作：隨機選擇1個交叉點r，把每個染色體分成2個子集，前面子集中的元素及順序不變，后面子集相互交換元素。

2.5 變異操作

可使用位移變異法，即在可行染色體中隨機選擇基因串，插入隨機選定的位置。由于變異操作只是產生基因位置的改變，所以變異后的染色體仍然滿足可行性準則。

3 實驗及其結果分析

某公司下設3個工廠生產某種產品，每日的產量分別是O1=7 t，O2=4 t，O3=9 t，該公司把生產的產品運往4個銷售點，各個銷售點每日的銷量為D4=3 t，D5=6 t，D6=5 t，D7=6 t。已知從各個工廠運往各個銷售點的單位可變成本和固定成本見表1，求總運費最少的運輸方案。

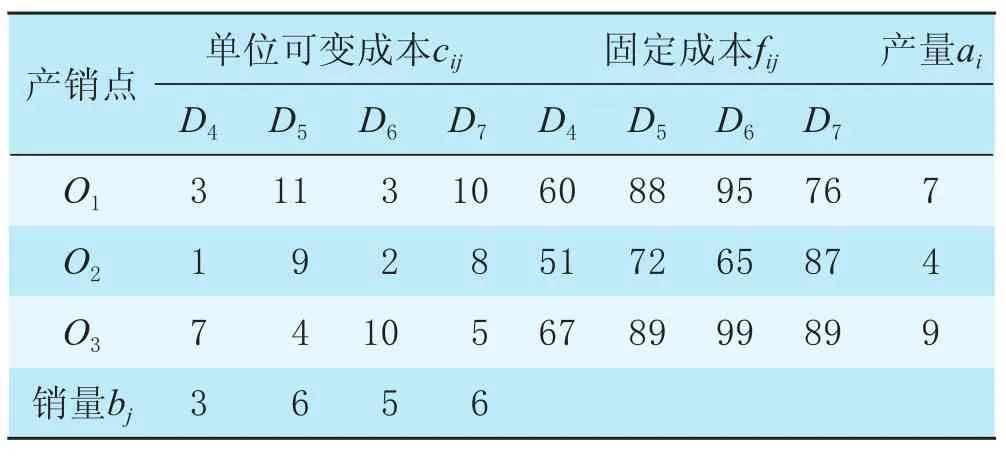
表1 產量、銷量、單位可變成本和固定成本表

求解步驟：

（1）根據題意建立數學模型，確定適應函數。

（2）按可行性規則，在java程序環境下在{1,2,…,7}中隨機可重復地選取5個數字生成初始可行性染色體，進而組成初始種群，本文可選取種群規模為30。

如某一個初始染色體為{2,6,3,7,1}時，Lo=6，，即滿足可行性規則，對應的運輸樹見圖1，對應的運輸分配量見表2。

圖1 初始染色體{2,6,3,7,1}對應的運輸樹

表2 初始染色體{2,6,3,7,1}對應的運輸分配量

適應度為：(4×3+95)+(3×10+76)+(3×1+51)+(1×2+65)+(6×4+89)+(3×5+89)=551。

（3）選擇操作。父代種群中適應度最大的染色體在子代中至少出現1次，然后按照賭盤選擇的方式進行選擇操作。

（4）交叉操作。選用單點位移交叉，交叉概率為Pc=1。

如某一個初始染色體為{1,5,2,6,3}時，Lo=6，，即滿足可行性規則

對應的運輸樹見圖2，對應的運輸分配量見表3。

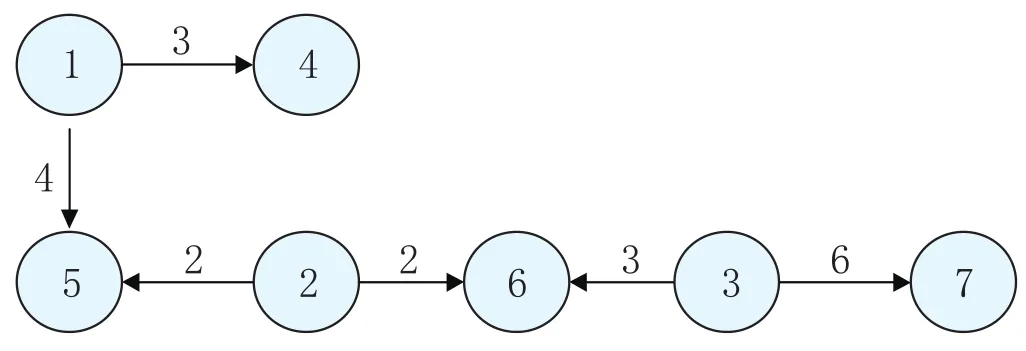
圖2 初始染色體{1,5,2,6,3}對應的運輸樹

表3 初始染色體{1,5,2,6,3}對應的運輸分配量

符合可行性準則的父代染色體通過交叉操作總可產生可行的子代，通過解碼得到相應的運輸樹。

例如：父代1＜2,6,3,|7,1＞和父代2＜1,5,2,|6,3＞通過交叉操作，得到子代1＜2,6,3,|6,3＞和子代2＜1,5,2,|7,1＞。

對于子代1＜2,6,3,|6,3＞，Lo=5，=1，LD=3，=3，滿足可行性準則，子代1的解碼圖見圖3。

圖3 子代1的解碼圖

由于x26=0，x36=0，節點7還需求3個單位，而節點1還有2個單位沒有分配，節點2還有1個單位沒有分配，所以增加邊(1,7)和（2,7），x17=2，x27=1。對應的運輸樹如圖4表示。

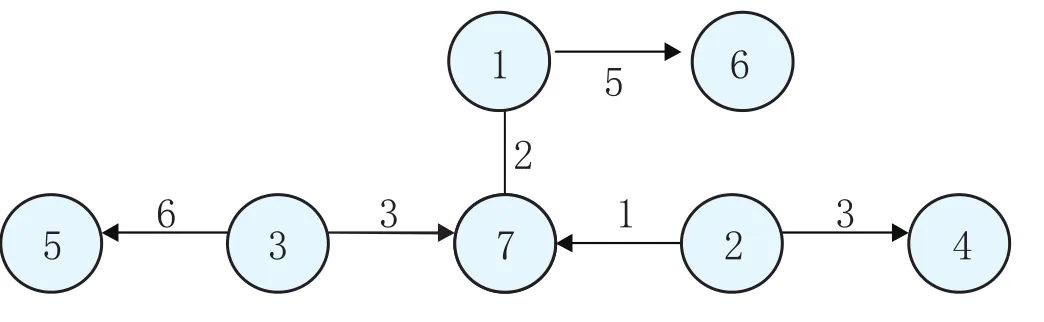
圖4 子代1的運輸樹

對于子代2＜1,5,2,|7,1＞，Lo=5，=1，LD=4，=2，即滿足可行性規則，子代2對應的運輸分配量見表4。

表4 子代2＜1,5,2,|7,1＞對應的運輸分配量

同理，由于x17=0，x25=0，節點7還需求2個單位，節點6還需求1個單位，而節點3還有3個單位沒有分配，所以增加邊(3,6)和（3,7），x36=1，x37=2。子代2的運輸樹見圖5。

圖5 子代2的運輸樹

（5）變異操作。使用位移變異規則，變異概率選取Pm=1/6。最大代數目取M=100。通過上述遺傳操作過程，可以得出該問題的最優染色體為{3,5,2,6,1}，解碼得：x16=6,x17=7,x25=0,x26=4,x34=3,x35=6,目標函數值為508。

4 結論

遺傳算法是模擬自然選擇和生物進化遺傳過程而提出并發展起來的搜素算法，此法能以較大概率尋求到問題的最優解，因而受到不同領域研究人員的重視[5]。本文針對固定費用運輸問題的特點提出基于運輸樹的遺傳算法，給出了能表示基解的染色體編碼方法，制定了染色體有效性判斷規則，并通過計算機程序生成有效初始種群，利用選擇、交配、變異規則最終得出滿意解。最后運用實例對算法的有效性進行了驗證。

[1] Murty KG. Solving the fixed charge problem by ranking the extreme points[J]. Operations Research，1968，16：268-279.

[2] Palekar US, Karwan MK, Zionts S. A branch-and-bound method for the fixed charge transportation problem[J].Management Science，1990，36(9)：1092-1105.

[3] 郭耀煌. 運籌學[M]. 成都：西南交通大學出版社，2000.

[4] 玄光男，程潤偉. 遺傳算法與工程優化[M]. 北京：清華大學出版社，2005.

[5] 刑文訓，謝金星. 現代優化計算方法[M]. 北京：清華大學出版社，1999.