基于離散指數函數優化GM(1,1)模型的重新優化

陳鵬宇 段新勝

(中國地質大學(武漢)工程學院,武漢 430074)

灰色預測模型是灰色理論的重要組成部分,而GM(1,1)模型是灰色預測模型中最基本的預測模型,已經在許多領域得到了廣泛應用[1-3].但是GM(1,1)模型在許多情況下預測精度并不高,即使擬合純指數序列也得不到滿意的結果,因此一些學者對其進行了研究[4-13],包括初始值確定[4-5]和背景值構造兩方面[6-13].初始值確定雖然在一定程度上影響了GM(1,1)模型的預測精度,但是最主要的精度影響因素還是背景值構造的缺陷.文獻[7-8]以拉格朗日中值定理在理論上分析了背景值構造的不足,文獻[9]從幾何思想上分析了背景值構造的不足,文獻[10-12]從積分思想上分析了背景值構造的不足,文獻[13]在非嚴格等比數列的基礎上對積分思想的背景值構造進行進一步優化.本文將基于文獻[13]提出的非嚴格等比數列(文中稱之為近似指數序列)思想,重新審視文獻[12]中的背景值構造,并指出文獻[13]優化方法的不足,建立新的背景值構造形式.實例應用結果顯示,新背景值構造形式下的GM(1,1)模型具有更高的精度.

1 GM(1,1)模型建模機理及其缺陷

令x(0)為GM(1,1)建模序列

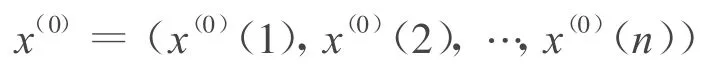
令x(1)為x(0)的AGO 序列

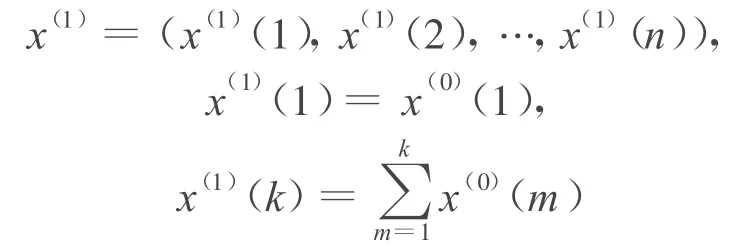
令z(1)為x(1)的均值(MEAN)序列

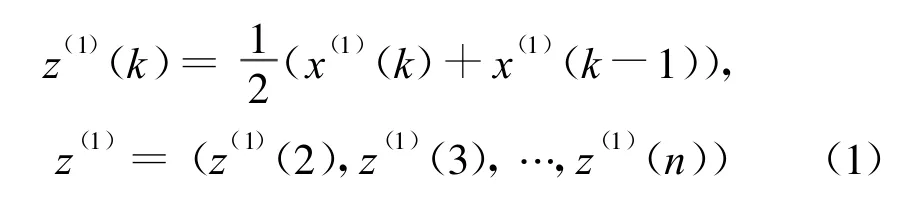
則GM(1,1)的定義型,即GM(1,1)的灰微分方程模型為

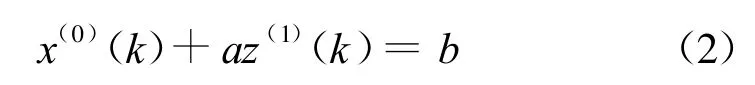
式中,a為發展系數,b為灰作用量,是微分方程的參數.

灰微分方程白化型為

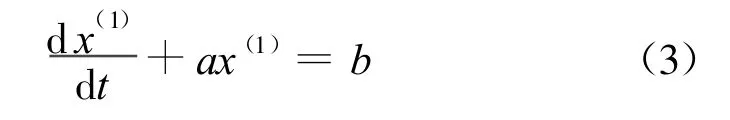
GM(1,1)白化型響應式為

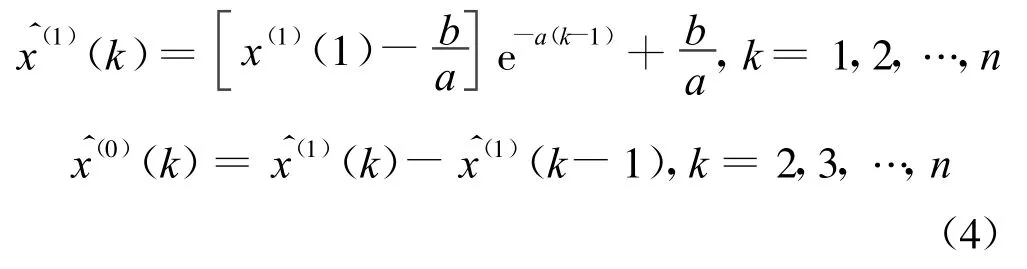
由最小二乘法,可以求得參數

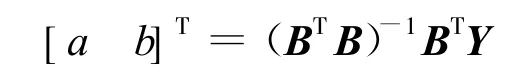
在區間[k-1k]上對灰微分方程白化型兩邊積分[12]:

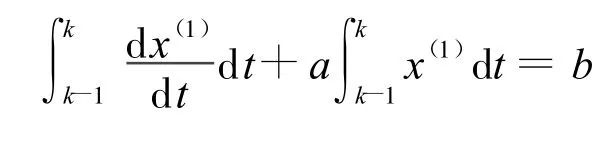
即

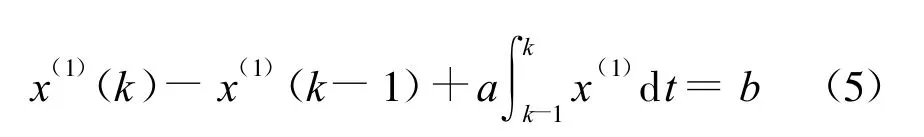
將式(5)與灰微分方程x(0)(k)+az(1)(k)=b比較可以得到兩者的差別僅為x(1)(k-1)),顯……