基于ADAMS的雙半內圈角接觸球軸承動態性能分析
謝鵬飛,蘇 敏,姜艷紅,梁曉東,鄧四二
(1.河南科技大學 機電工程學院,河南 洛陽 471003;2.洛陽LYC軸承有限公司,河南 洛陽 471039;3.寧波達克軸承有限公司,浙江 寧波 315000)
高速雙半內圈角觸球軸承是航空發動機主軸常用的一種高速、高定位精度軸承。該軸承工作條件苛刻、轉速高(dmn≥1.5×106mm·r/min),其動態性能直接影響到發動機的性能。因此,對雙半內圈角接觸球軸承的動態特性參數分析非常重要。國內、外對高速角接觸球軸承的研究分析,先后經歷了靜力學分析、擬靜力學分析、擬動力學分析及動力學分析4個階段,并在此基礎上開發了一系列的分析軟件。如國外SKF/NASA開發的CYBEAN,Gupta開發的ADORE[1],Aramaki為NSK公司開發的BRAIN[2],Stacke為SKF開發的BEAST[3]等;國內較為成熟的有RODTAN和ROQDAN[4]。目前存在的問題是大多數軸承分析軟件中不考慮保持架整體變形對軸承性能的影響;而高速雙半內圈角接觸球軸承保持架的梁尺寸較小,整體結構柔性較大,其整體的彈性變形已經影響到了軸承的動態性能。
鑒于此,這里將保持架作為柔性體,基于ADAMS系統[5-6]建立雙半內圈角接觸球軸承剛柔耦合仿真分析模型,對該軸承類型進行動態特性分析。
1 數學分析模型
雙半內圈角接觸球軸承在運動過程中內部的動力學特性非常復雜。現進行如下假設:(1)外圈固定,內圈繞其軸線轉動且可三維平動,保持架和鋼球可任意轉動和平動;(2)模型中各剛性元件幾何變形僅存在于局部接觸位置,且接觸變形符合Hertz接觸理論;(3)在完全彈流潤滑狀態下計算彈性流體動力潤滑拖動力。
1.1 鋼球與溝道間作用力
1.1.1 法向接觸力
由Hertz理論可知,鋼球與溝道之間的法向接觸力為[7]:
Q=Kδ1.5
(1)
式中:K為某鋼球與溝道接觸處的載荷-變形常量;δ為某鋼球與溝道之間彈性變形量。
圖1為鋼球與內、外溝道的接觸角,變形和位移幾何圖。圖1中Ob為位移后鋼球中心;Oe為外溝道曲率中心(靜止不動);Oi0為內溝道位移前曲率中心;Oi為內溝道位移后曲率中心。由圖1中幾何關系可得:
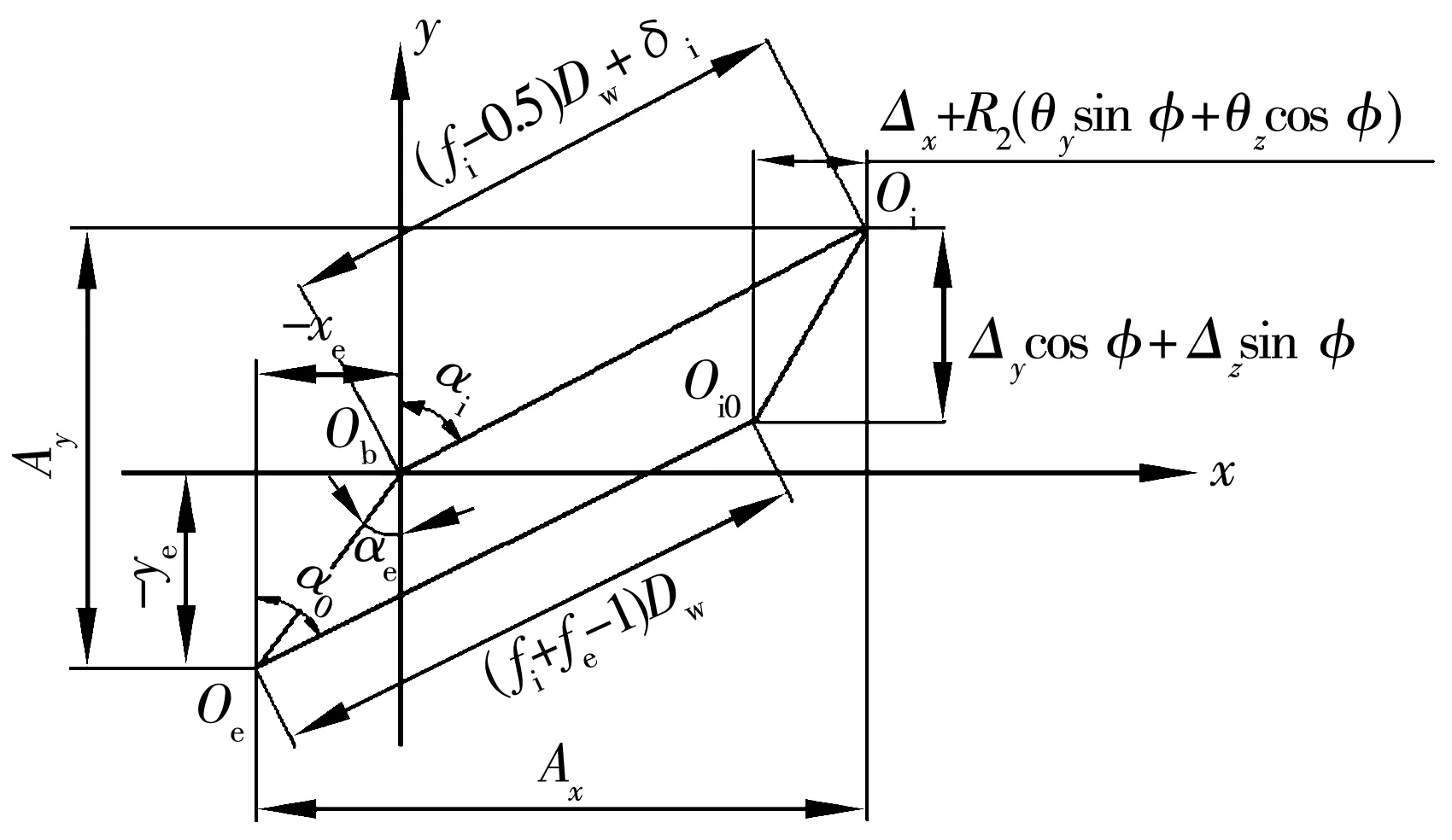
圖1 接觸角、變形和位移幾何圖
Axj=[(fi+fe-1)Dw]sinα0+[Δx+R2(θy·
sinφj+θzcosφj)]
=[(fi-0.5)Dw+δij]sinαij+[(fe-0.5)·
Dw+δej]sinαej
(2)
Ayj=[(fi+fe-1)Dw]cosα0+[Δycosφj+
Δzsinφj]-Pd
=[(fi-0.5)Dw+δij]cosαij+[(fe-0.5)·
Dw+δej]cosαej
(3)
式中:Dw為鋼球直徑;fi,fe分別為內、外溝道曲率半徑系數;R2為內溝道溝曲率中心圓半徑;Δx,Δy,Δz分別為內圈在x,y,z方向上的位移;α0為軸承原始接觸角;αij,αej分別為第j個鋼球與內、外溝道間的工作接觸角;δij,δej分別為第j個鋼球和內、外溝道間的彈性變形量;Pd為軸承裝配、溫度變化、軸承轉速引起的軸承徑向方向的間隙變化量;θy,θz為轉動套圈相對于靜止套圈在y,z軸方向的偏斜角;φj為第j個鋼球的位置角。
由(2)~(3)式及圖1中幾何關系可得:
(4)
αej=arctan (xej/yej)
(5)
(6)
αij=arctan [(Ax-xej)/(Ay-yej)]
(7)
式中:xej,yej為外溝曲率中心Oe與鋼球中心Ob在x,y方向上的距離。
1.1.2 鋼球與溝道間的摩擦力
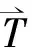
(8)
(9)
(10)
Tmζ(η)nj=(uEHDmQm)ζ(η)nj
(11)
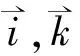
1.2 鋼球與保持架兜孔間的法向作用力
鋼球在內、外溝道空間中的運動一般可分解為兩部分:(1)鋼球質心在軸承全局坐標系中的平動;(2)鋼球繞質心在鋼球局部坐標系中的轉動。一般來說,在軸承運轉時,鋼球中心與兜孔中心不重合。圖2示出了兜孔中心超前于鋼球中心和滯后于鋼球中心的情況。

圖2 鋼球質心與兜孔中心的運動關系
在SHABERTH的第5代角接觸球軸承試驗模型基礎上引入鋼球與保持架間的彈性變形量。保持架兜孔與鋼球間法向作用力的計算式為[9]:
(12)
式中:Kc為試驗數據確定的線形逼近常量,對于球軸承Kc=11/Cp;Cp為保持架兜孔間隙,Cp=0.5×(Dp-Dw),Dp為保持架兜孔直徑;Kn為鋼球和保持架兜孔接觸處的載荷-變形常量;zcj為第j個兜孔的中心位移。
1.3 保持架與引導套圈間作用力
保持架與引導套圈間的相互作用是由潤滑劑的流體動壓效果所產生的。由流體動壓油膜的分布壓力產生的作用于保持架的合力Fc可用兩個正交分量Fcy′和Fcz′來描述,如圖3所示。
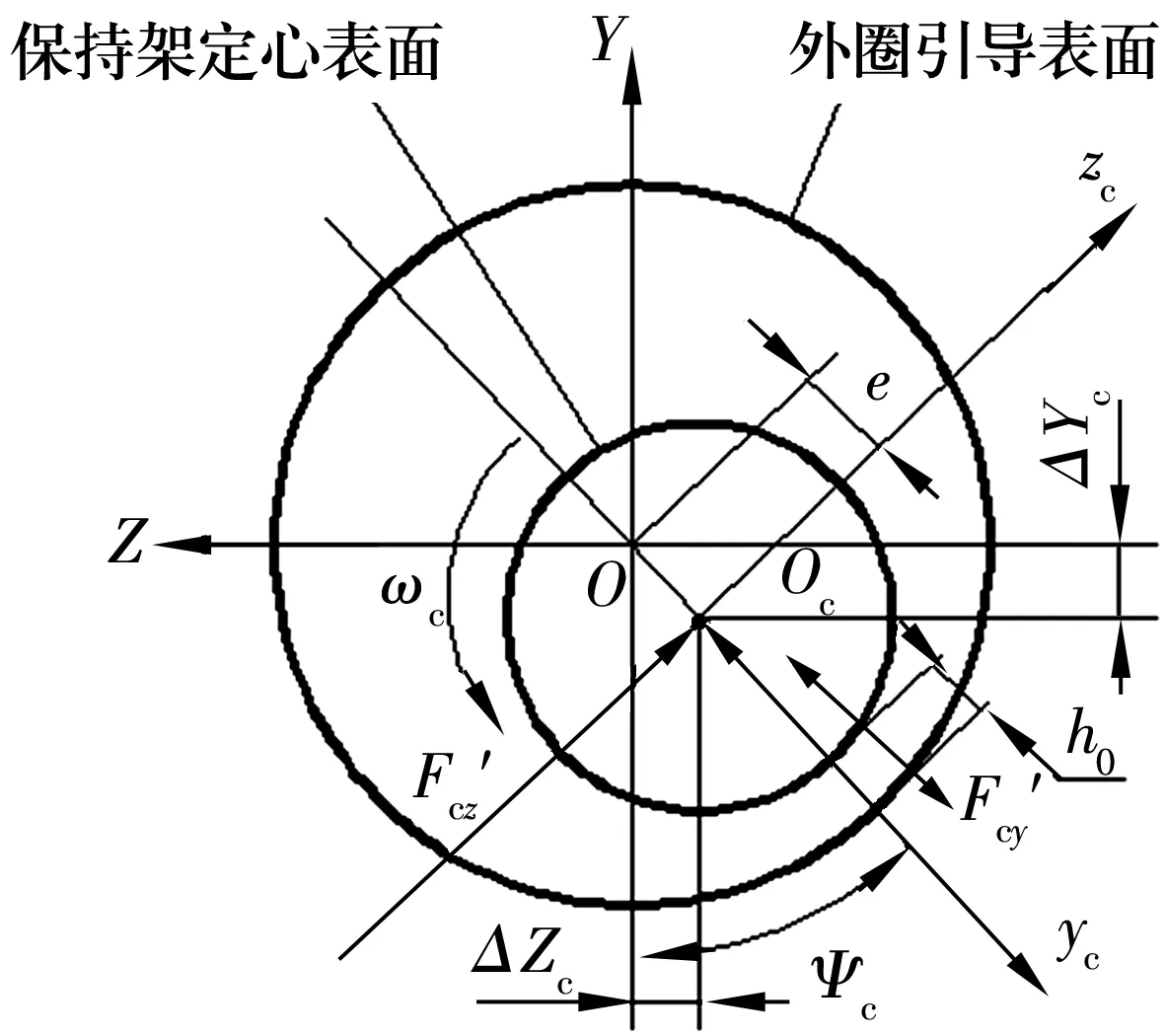
圖3 外圈引導擋邊與保持架的幾何構形
圖3中,平面坐標系sc={Oc,yc,zc}固定在保持架上,坐標中心點Oc位于保持架質心,yc軸正好通過最小油膜厚度h0所在的點,與慣性坐標軸Y的夾角為Ψc。
(13)
(14)
式中:η0為大氣壓力和環境溫度下潤滑油的動力黏度;u1為潤滑油拖動速度;L為保持架定心表面寬度;C1為保持架引導間隙;ε為保持架中心的相對偏心量,ε=e/C1;e為保持架中心的偏心量。
2 仿真與分析
2.1 剛柔耦合擬動力學仿真建模
利用ADAMS系統內部cmd語言編制雙半內圈角接觸球軸承參數化剛柔耦合仿真模塊,用戶只需輸入軸承的結構參數即可自動生成所要分析軸承的剛柔耦合三維實體模型。
根據上述軸承數學分析模型,采用程序設計語言FORTRAN編寫軸承零件間作用力的子程序,如表1所列。所編寫的子程序通過其編譯生成的動態鏈接庫*.dll文件與ADAMS/Solver相鏈接,在ADAMS中完成雙半內圈角接觸球軸承剛柔耦合擬動力學仿真分析。

表1 子程序列表
2.2 算例分析
某型號雙半內圈角接觸球軸承主要結構參數與工況參數如表2所示。將表2中各參數輸入所編制的雙半內圈角接觸球軸承剛柔耦合擬動力學仿真模塊中,生成三維剛柔耦合模型(圖4),并進行擬動力學仿真計算。圖4中將軸承右半內圈隱藏,外圈的透明度增加,外連點在保持架的中心位置,一維單元為外連點與保持架內壁間的均布單元。
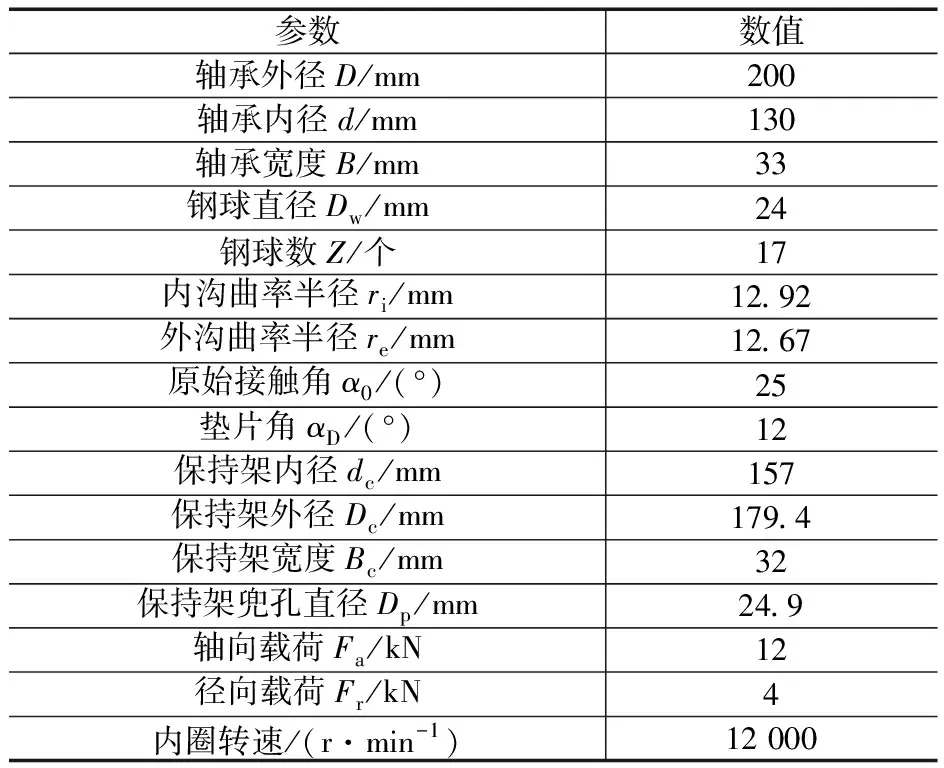
表2 軸承主要參數
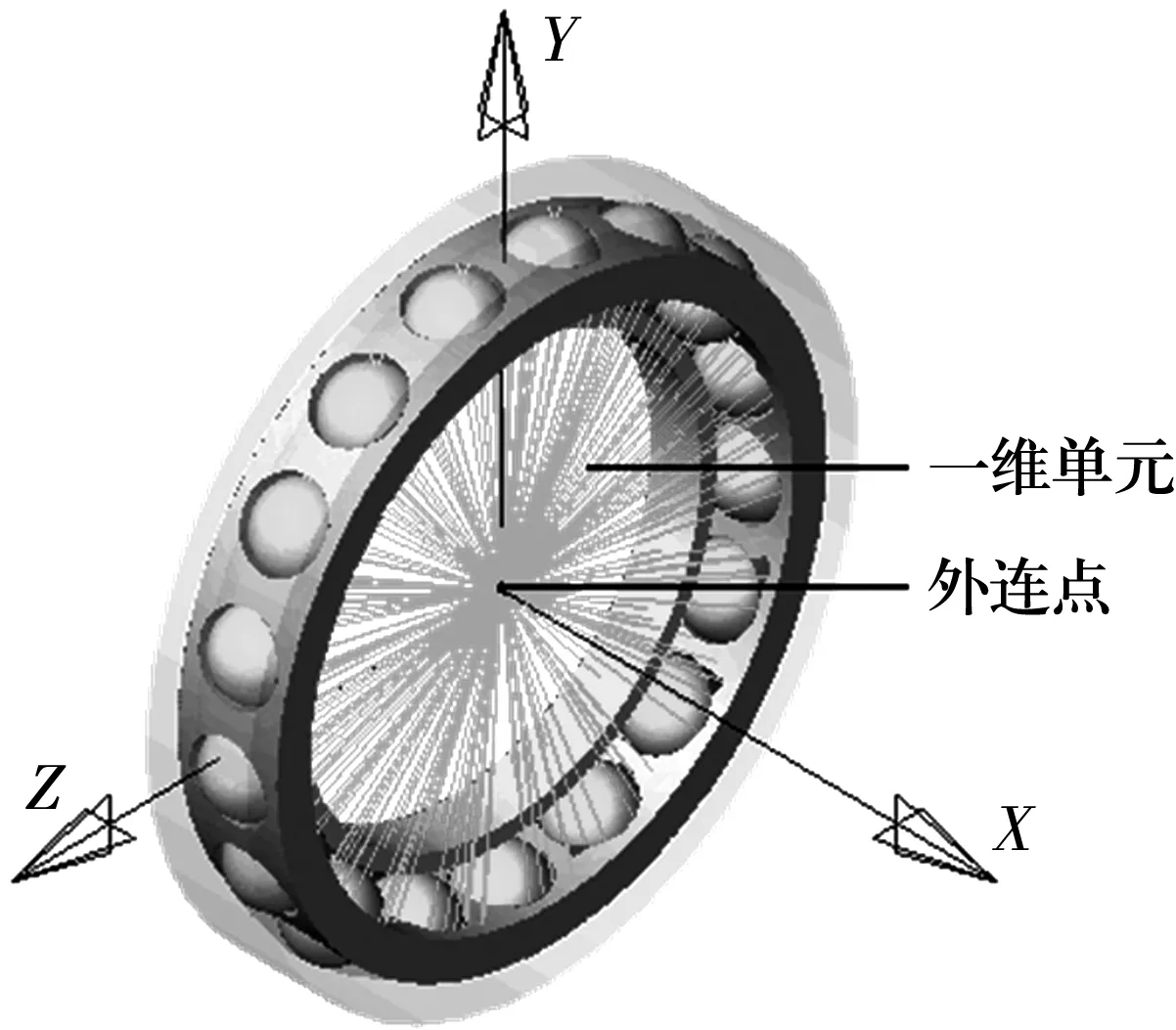
圖4 雙半內圈角接觸球軸承剛柔耦合模型
利用后處理模塊(ADAMS/PostProcessor)查看仿真結果,并進行分析討論。
圖5為鋼球1與內、外溝道的接觸應力隨時間的變化曲線,由圖5可知:在高速下,鋼球所受的離心力導致外接觸角減小而內接觸角增大,間接使外接觸力大于內接觸力,從而造成外接觸應力大于內接觸應力;同樣受到徑向載荷的影響,接觸應力呈正弦波動。外接觸應力最大值為1 668.35 MPa,平均值為1 558.64 MPa;內接觸應力最大值為1 348.90 MPa,平均值為1 169.18 MPa。
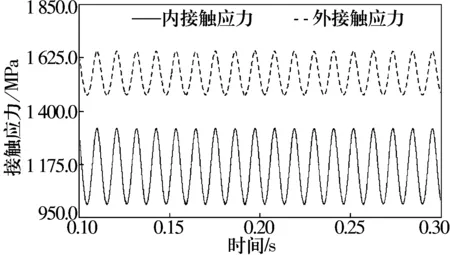
圖5 鋼球與內、外溝道接觸應力
穩定狀態下鋼球與保持架兜孔間作用力曲線如圖6所示。結合圖5和圖6可知:在鋼球進入和離開徑向載荷區域時,鋼球與保持架兜孔間的作用力較大。這是由于在鋼球進入和離開徑向載荷區域時,鋼球與保持架的速度不一致,從而使鋼球與保持架間發生碰撞,作用力增大。鋼球1與保持架兜孔間的作用力最大值為35.5 N,平均值為7.9 N。
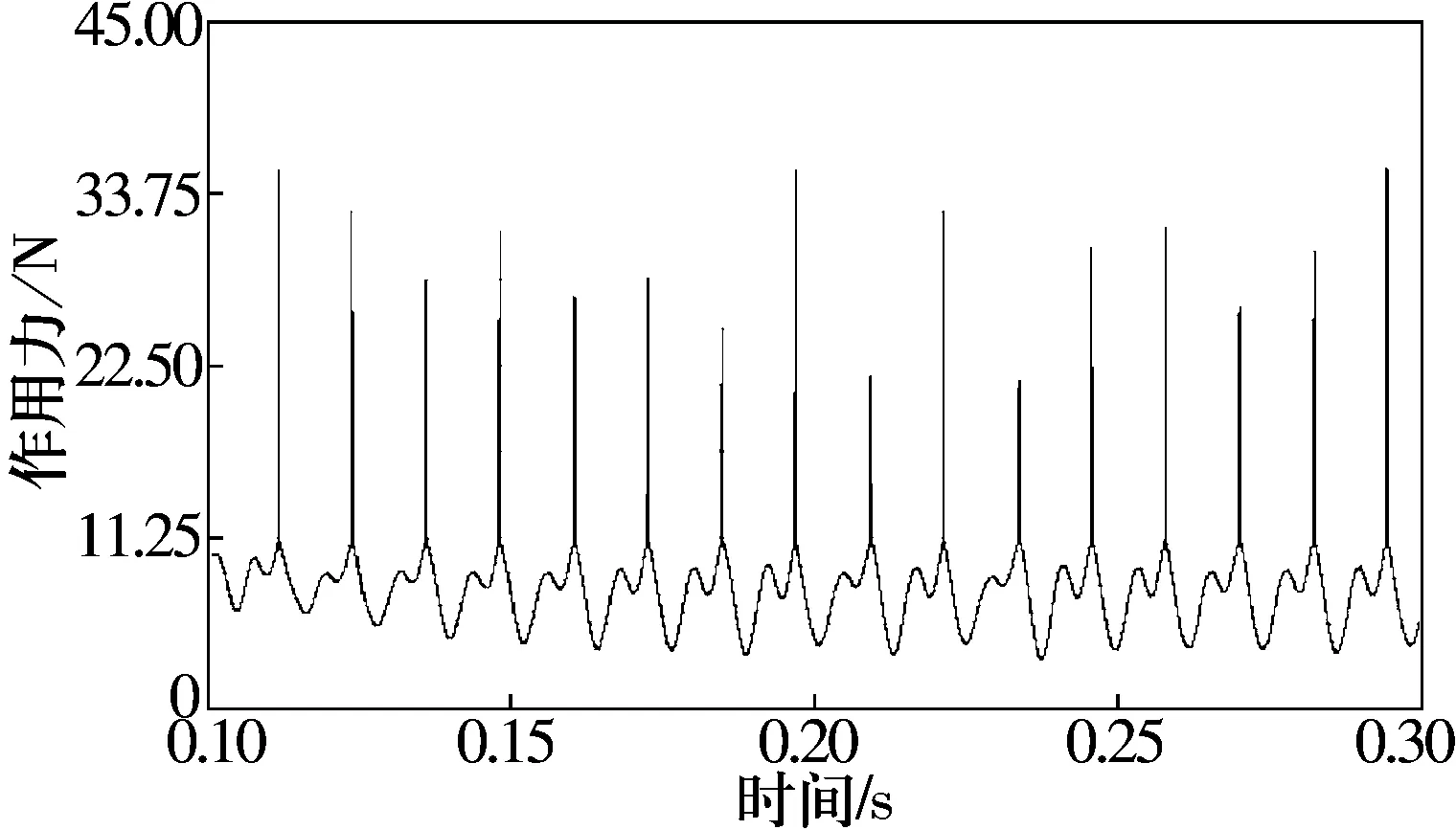
圖6 鋼球與兜孔間作用力
圖7為軸承運轉穩定后引導套圈與保持架間作用力Fc隨時間的變化曲線。由圖7可知:Fc的最大值為32.94 N,平均值為20.82 N。
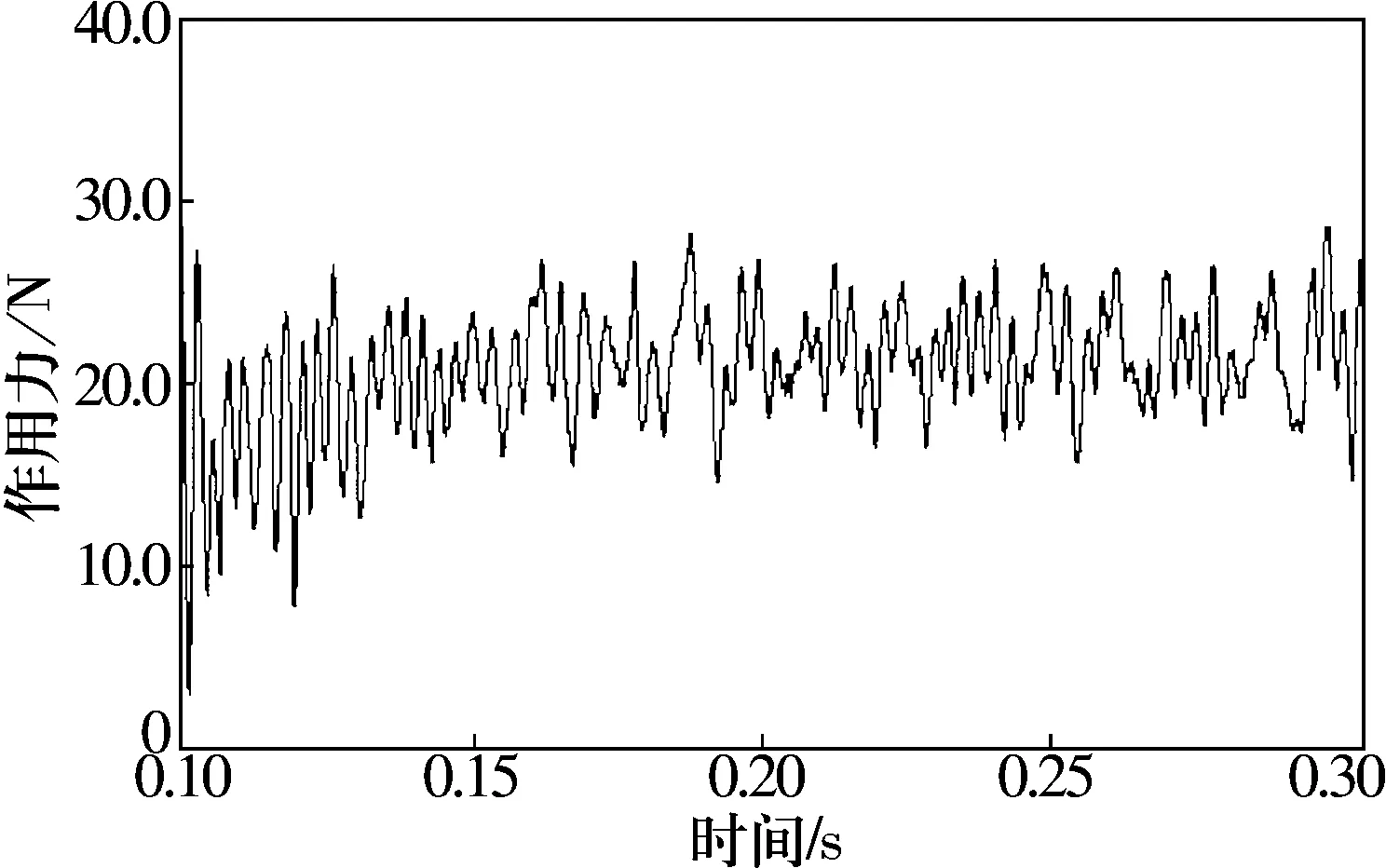
圖7 保持架與引導套圈間作用力
保持架在鋼球、引導套圈以及自身離心力的聯合作用下,內部將會產生局部的應力集中。圖8為軸承保持架側梁上某節點的當量應力(Von mises應力)關于時間歷程的曲線圖。由圖8可知:軸承運轉穩定后,該節點的當量應力穩定在91.3 MPa左右。
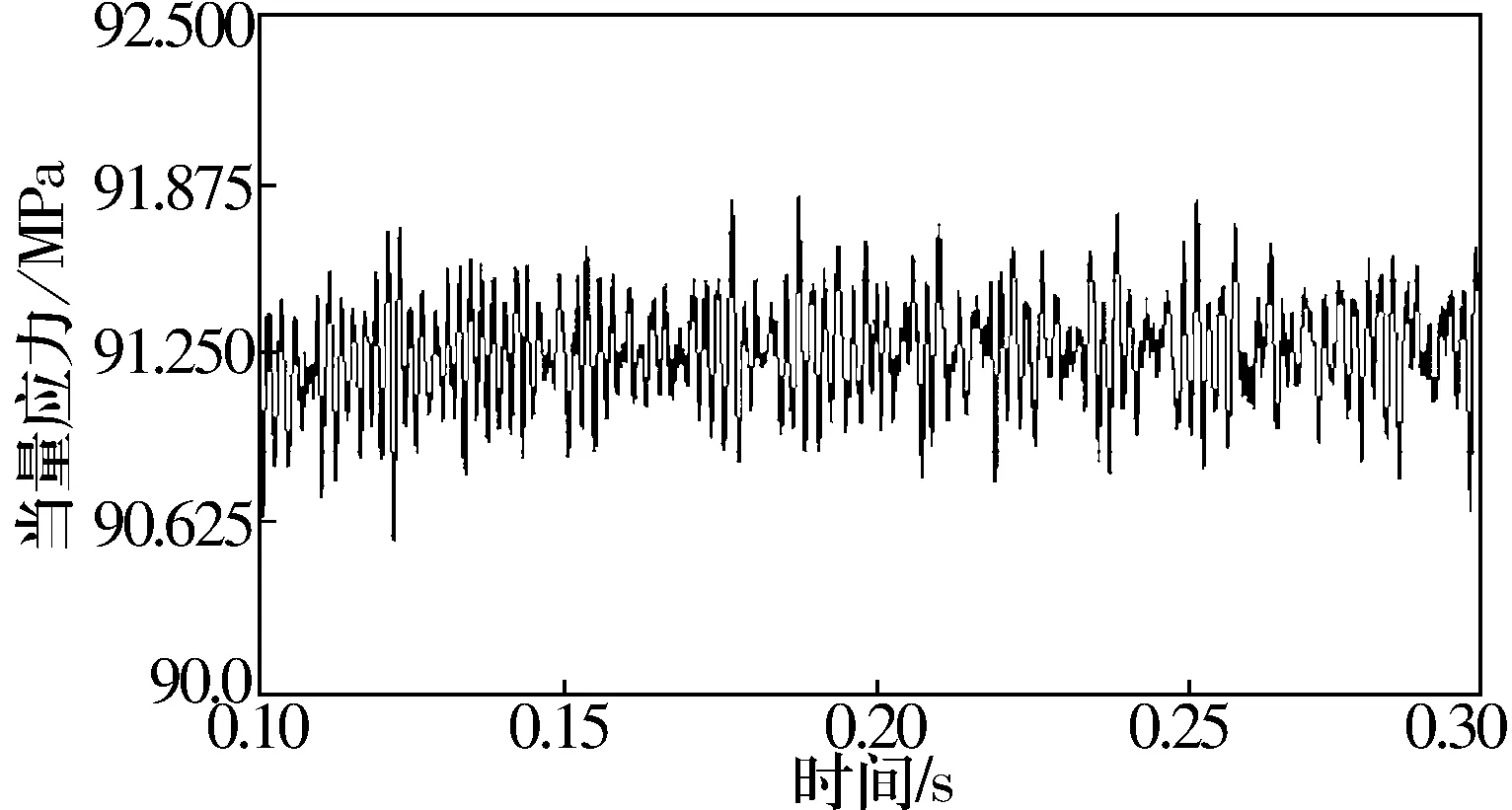
圖8 保持架側梁某節點當量應力
2.3 柔性保持架與剛性保持架對比
為了分析保持架整體彈性變形對軸承動力學性能的影響,在建立柔性保持架時保留被離散化處理的剛性保持架,通過設定兩者的有效和無效,進行了對比仿真分析。
圖9為鋼球與保持架兜孔間作用力的對比曲線。由圖9可知:柔性保持架與鋼球的作用力明顯小于剛性保持架;這是由于在鋼球與保持架發生碰撞時,柔性保持架的整體彈性變形吸收了部分能量,從而導致柔性保持架與鋼球的作用力小于剛性保持架。剛性保持架的最大值為52.4 N,柔性保持架的最大值為35.5 N。
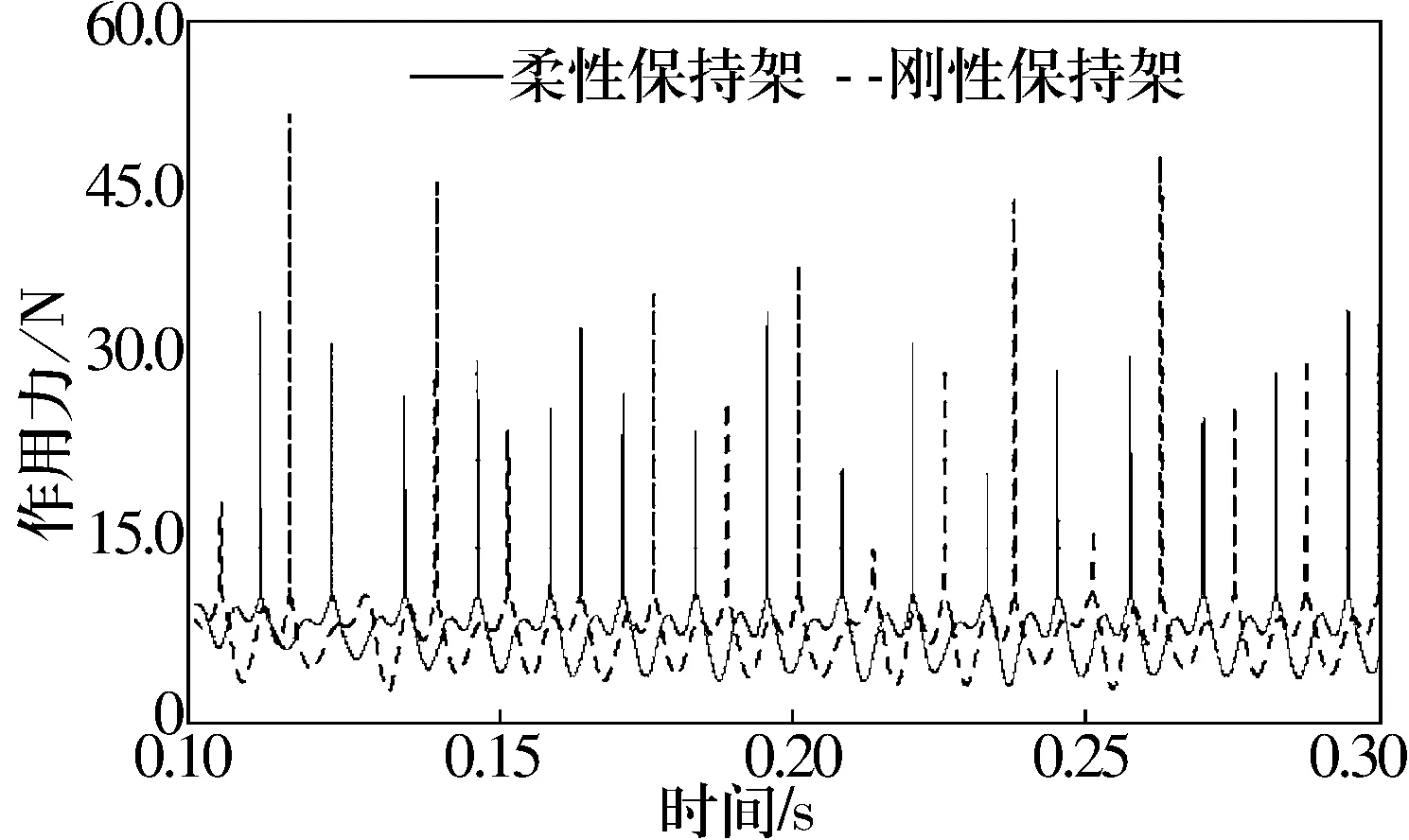
圖9 鋼球與兜孔間作用力對比
保持架質心軌跡是評定保持架穩定性的重要參數,質心軌跡越規則,保持架運轉越穩定。圖10為保持架質心軌跡對比曲線。由圖10可知:柔性保持架的質心軌跡非常規則,接近于圓形,而剛性保持架的質心軌跡比較混亂。這是由于柔性保持架的整體彈性變形抑制了保持架的振動,從而使自身運轉更加穩定。

圖10 保持架質心軌跡
3 結束語
(1)在軸向、徑向聯合載荷作用下,雙半內圈角接觸球軸承鋼球與內、外溝道間的接觸應力呈正弦波動。
(2)在鋼球進入和離開徑向載荷區域時,鋼球與保持架的速度不一致,從而導致兩者間的作用力發生周期性突變。在軸承運轉穩定后,保持架與引導套圈之間的作用力在小范圍內波動。
(3)在保持架運轉過程中,柔性保持架的整體彈性變形吸收了部分能量并抑制了保持架的振動,使其自身受力更小,運轉更平穩。
這里所編制的軟件在軸承擬動力學分析的同時,可對柔性保持架進行瞬態應力分析,為提高軸承動力學分析精度提供了一定的參考價值。

