基于小波變換的時間序列奇異性問題探析

李炳林 ,向書堅

（1.湖南科技學院 經管系,湖南 永州 420010；2.中南財經政法大學a.信息學院；b.研究生部，武漢 430060）

0 引言

經濟現象的運行規律一般具有趨勢性與周期性，對其規律性的研究主要是通過對經濟現象的時間序列數據進行觀察，尋找其運行過程中的變異點，即對應時間序列的奇異點（拐點）。筆者認為經濟現象時間序列的有關數據可以抽象為信號（函數），而經濟現象變化的奇異點（拐點），則可抽象為信號（函數）的奇異點的檢測。通過檢測時間序列（信號）的奇異性和位置（時間），來研究經濟現象運行的周期性及變化趨勢。傳統的奇異性檢測方法是基于Fourier變換,它只能反映信號奇異性的整體性質,很難確定各奇異點的位置及各奇異點奇異性的強弱。而小波變換具有良好的時頻局部化特性,能更好地分析信號的奇異點的位置及奇異性的強弱。奇異點的位置可以通過跟蹤小波變換在小尺度下的模極大曲線來檢驗；信號奇異點奇異性的強弱可以由小波變換模隨尺度參數的衰減性和Lipschitz指數來刻畫。因此，我們利用二進小波變換模極大值和Lipschitz指數來探測時間序列奇異點的位置與奇異點的強弱。

1 小波及小波變換

定義 1 對?Ψ（t）∈L2(R)，設 Ψ（t）的 Fourier變換為Ψ滿足容許條件：

則稱 Ψ（t）是一個基本小波或小波母函數。 由 CΨ＜+∞ 知，反之，若 Ψ（t）滿足|ψ(t)|≤c(1+|t|)-1-ε(ε＞0)，且其中 c 是一個常數，則式（1）成立。 說明小波函數不僅要求具有一定的震蕩性，即包含著某種頻率特征，而且還要求具有一定的局部性，即在一個區間上恒等于0或很快地收斂于0，這也就是Ψ（t）稱為小波的原因。

定義 2 對于小波函數 Ψ（t），函數 f(t)∈L2(R),f(t)的小波變換定義為：

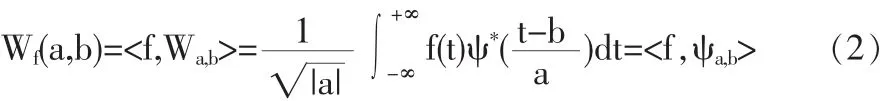
其中 a≠0，b、t均為連續變量，ψ*(t)表示 Ψ（t）的復共軛。小波變換定義為信號和小波函數ψa,b(t)的內積，表示了信號與小波基函數的相似程度。

2 序列（信號）的奇異性

2.1 Lipschitz指數的概念

定義 3 設 f(t)∈L2(R)，如果存在常數 Kv＞0及 m[α]次多項式pv使得：

稱函數 f(t)在點 v 是 Lipschitzα(α≥0)。

定義4 如果在[a，b]上存在與 v無關的常數K＞0，使得（3）式對所有的 v∈[a,b]成立，則稱 f(t)在[a，b]上是一致 Lips?chitzα。

由上述定義，我們有以下結論：如果函數f(t)在v點的Lipschitz指數α小于1，那么稱函數f(t)在v點是奇異的。若函數 f(t)的Lipschitz指數 α'滿足 n＜α'＜n+1，則 f(t)在 v 點是 n次可微的，但其n次導數f(n)(t)在v點是奇異的，它的Lipschitz指數為α'-n，也稱α'描述了這個奇異性。如果f(t)的原函數F(t)在 v 點的 Lipschitz指數為 α+1(-1≤α＜0)，則稱 f(t)在點 v是Lipschitzα。負的Lipschitz指數意味著函數具有比不連續（α=0）更大的奇異性。特別地有，若函數f(t)在v點連續可微，則函數 f(t)在v點的Lipschitz指數為1；若函數 f(t)在 v點可微，而導數有界但不連續，f(t)在v點的Lipschitz指數為1；若函數f(t)在v點不連續但有界，則f(t)在v點的Lipschitz指數為0。

因此，Lipschitz指數α刻畫了f(t)在v點的光滑程度，α值越大，函數越光滑，奇異性越小；反之，α值越小，表明函數在該點處變化越尖銳，奇異性越大。

2.2 小波變換模極大值

Mallat等通過分析小波變換模的局部極大值與函數奇異性的關系發現，小波變換模|Wf(s,u)|的衰減性可以由其局部極大值控制，可以利用小波變換模|Wf(s,u)|（其中s為尺度）在v的鄰域中的衰減性來刻畫函數f(t)在點v的局部Lipschitz正則性。

定理 1[1]設 f(t)∈L2(R)在區間 [a，b]上是一致Lipschitzα≤n,則存在 A＞0，使得：

反之，設f(t)是有界且對某個非整數有α＜n，使得|Wf(s,u)，則對?ε＞0，f(t)在[a-ε,a+ε]上是一致 Lipschitzα。

定理1說明，對v0領域內的任意點v，若在尺度s上滿足|Wf(s,v)|≤|Wf(s,v0)|，則稱(s,v0)為一模極大值點，|Wf(s,v0)|稱為在點(s,v0)點的小波變換模極大值。若在二維平面（s，v）上某一曲線上的點均為模極大值，則稱此曲線為極大值線。

定理 2 設 f(t)∈L2(R)在 v0處是 Lipschitzα≤n，則存在A＞0，使得反之，若 α＜n，使得為非整數，且存在 A＞0 和 α'＜α 使得則 f(t)在 v0是 Lipschitzα。

上述定理說明了f(t)在v0的局部Lipschitz正則性依賴于在v0的領域中Wf(s,v)在細尺度下的衰減性。由（4）得：|Wf(s,因此當信號的奇異指數α＞0時，其小波變換模隨尺度s的增加而增大；當奇異指數α＜0時，小波變換模隨尺度s的增加而減少。

2.3 序列（信號）奇異點的判定

定理3 （HWANG，MALLAT）設n是一個嚴格的正整數，θ(t)是一個平滑函數，ψ(t)是一個緊支撐的n次連續可微的小波函數，且 ψ=(-1)nθ(n)，對于 f(t)∈L1(a,b)，如果存在 s0＞0，使得對任意的 s＜s0和 u∈[a,b]，|Wf(s,u)|沒有局部極大值，則對?ε＞0，f(t)在[a-ε,a+ε]上是一致 Lipschitz n 的。

定理3說明了如果小波變換Wf(s,u)在細尺度下沒有極大值，那么f(t)一定是局部正則的。它缊含了如下事實：僅當存在一個小波極大點序列 (sp,up)p∈N在細尺度下收斂于v，即則 f(t)在 v 點是奇異（非 Lipschitz 1）的。另外，僅沿著尺度搜尋小波模極大值點對于奇異性檢測還是不充分的，還需要從模極大值的衰減性計算函數在一點的Lipschitz正則性。

定理 4 對于 s＜s0，設函數 f(t)定義在區間（a,b）上，如果收斂于v的所有模極大點都包含在錐|u-v|≤Cs中，則對小于n的非負整數α，函數f(t)在v點為Lipschitzα，當且僅當存在常數 A＞0，使得|u-v|≤Cs中的模極大點滿足即

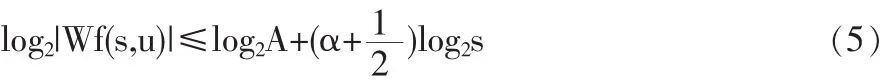
定理 4說明了f(t)在點 v的 Lipschitz α就是 log2|Wf(s,u)|作為log2s的函數沿著收斂于v的極大曲線的最大斜率減去1/2。這為我們提供了一種簡便計算Lipschitz指數α的方法。

3 序列（信號）的奇異性檢測

3.1 Lipschitz指數α的計算

（1）對時間序列做濾波處理

經濟現象在運行過程中，受各種因素的干擾，這些干擾因素可歸結為隨機因素，即噪聲，而噪聲都服從或近似服從高斯分布。由于白噪聲具有負的Lipschitz指數，且其幅度和稠密度隨尺度增加而減少；若小波變換局部模極大值及稠密度隨尺度的關注而快速增大，則說明該處的奇異性主要是由噪聲控制。因此，為了減少噪聲對分析的影響，必須進行濾波處理，消除噪聲的干擾。

設時間序列f(t)在t0處有奇異性，我們用Gauss型函數做濾波器處理，即：h(t)=f(t)gσ(t)。

（2）對 h(t)作二進小波變換

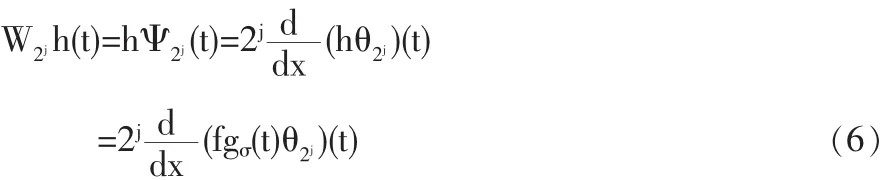
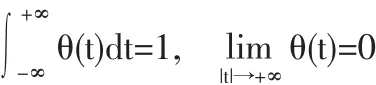
為簡單起見，假定函數θ(t)類似于 Gauss函數，θ(t)的形式為，則 gθ(t)仍為一Gauss函數，即：σ2j

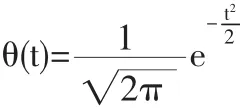
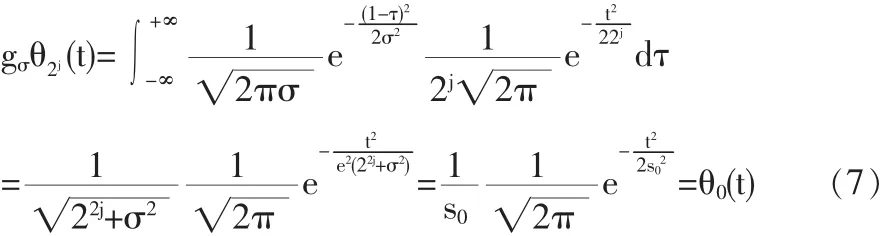
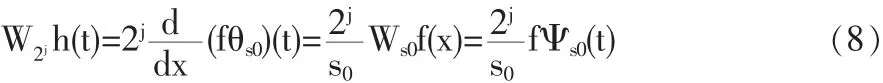
因此,有奇異性的序列（信號）f(t)被均方差為σ的Gauss函數平滑后，在尺度為2j時的小波變換等價于沒有平滑的奇異性函數在尺度為s0時的小波變換。于是這時,|W2jh(t)|≤

（3）建立目標函數，確定α的值

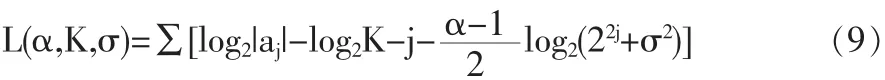
對aj使（9）式極小化就可確定σ、k和α的值。

3.2 由確定的α判斷f(t)的奇異性，根據尺度2j確定奇異點的位置（時間）

4 結束語

時間序列（信號）的奇異性包含經濟現象變化的最重要信息。小波變換能夠使其信息集中在幾個小波系數中，并且通過濾波消除噪聲的干擾，這樣就能準確找到序列的奇異點及其變化的時間，對于正確認識經濟現象變化規律具有重要意義。因此，用二進小波變換模極大值與Lipschitz指數來探測序列的奇異性不失為一種有用的方法。雖然小波分析近乎完美的數學特性受到各領域科學家和工程技術人員的青睞，但現在還沒有找到一種適用于每個領域或者不同領域的小波函數，在運用小波函數時，只能從已知的二十來種小波函數中去選擇、篩選找到最適合的小波函數。在具體研究序列的奇異性時，還要考慮消失矩與閥值。另外，小波變換廣泛運用于時間序列的相關性、長記憶性、非平穩性、區間估計、譜密度估計及分形等方面。我們相信，隨著小波理論的完善，小波分析在經濟領域的應用前景將會更加廣闊。

[1]Stephane Mallat,Wen Liang Hwang.Sigularity Detection and Processing with Wavelets[J].IEEE Transactions on Information Theory,1992,38(2).

[2]Mallat S,Zhong S.Characterization of Signals from Multiscale Edges[J].IEEE Trans on PA-MI,1992,14(7).

[3]Daubechies I.Ten Lectures on Wavelets[Z].CBMS-NSF Series in Appli.Math.,SIAM,1992.

[4]Donald B,Percival,Andrew T,Walden.Wavelet Methods for Time Series Analysis[M].北京：機械工業出版社，2006.

[5]孫成祥，晁勤.小波變換在信號奇異性檢測中的應用仿真研究[J],江西科學，2007,（2）.

[6]劉杰等.基于新閾值函數的二進小波變換信號去噪研究[J].東北大學學報(自然科學版),2006,(5).

[7]祝強等.小波特性對間斷點檢測的影響[J].陜西科技大學學報,2007,(8).