灰預測模式評估觀光農業之游客量

梁大慶,張俊斌

(1.臺灣虎尾科技大學,臺灣 云林 63201;2.臺灣中州科技大學,臺灣 彰化 51450)

1 前 言

時代的潮流與變遷,農業產業的轉型成了解決農業產業問題的重要方向。休閑農業將農村資源提供觀光游憩使用,以提高農民的所得與福祉,并增加游憩資源的供給,以滿足游客的需求。臺灣休閑農業的推展有兩個方向:其一為農業生產結構的提振,其二為休閑游憩機會的提供。為滿足休閑活動需求的增加與多樣化的要求等多方面考慮,于1993年起實施 “休閑農業區設置管理辦法”,隨著1996年 “休閑農業輔導辦法”的修正完成,休閑農業的推動也有顯著之發展。近年臺灣地區政治與經濟環境產生頗大的變化,所面對的環境亦不斷的變遷,相關的產業亦不斷地改變。以觀光旅游產業為例,餐飲、旅館、航空、運輸、旅行業等多項產業過去都是觀光產業的主干,而農業觀光休閑產業已被認為是未來發展的優先選擇[1],振興觀光還有助于活絡關聯產業。酒產業與酒文化向來與日常生活習習相關,在臺灣酒產業漸漸地影響地方生活文化,可說是帶動觀光產業的火車頭。南投埔里酒廠是臺灣的酒鄉,現已轉型為休閑觀光酒廠,設有酒文化館及產品展示中心,并結合當地觀光資源共同推展文化活動,以 “文化釀酒、藝術觀光”為主軸,配合鄰近觀光游憩景點,孕育旅游空間,活絡埔里的酒文化觀光特色,以吸引更多的觀光客到埔里來旅游和消費,埔里酒廠不僅是生產制造者,也是文化歷史保存者,更是觀光發展的推手[2]。雖自921震災重創后,使得南投地區觀光一落千丈,如今埔里酒廠為埔里地區觀光產業的重點區域,因此以埔里酒廠為例進行分析,實具有指標性之意義。

目前關于觀光旅游產業之預測,多半是透過單變量與多變量之解釋變量來建立預測模型。但傳統計量經濟學及統計分析需要龐大樣本數據作為建模的基礎,且必須符合統計上的相關檢定,才會有較佳的預測精確度;相較于灰色系統理論是針對系統模型之不確定性及信息之不完整性下,只需少量數據便可建立預測模型,灰色系統理論更為簡便[3]。因應科技時代的快速變化,以往需要收集大量數據樣本才能預測長期規律的預測模型,在現實環境中較沒效率;反而是樣本數據比較少,計算過程簡單,較具時效性的灰色預測模型漸漸地被廣泛應用于各領域中。H sing et al.將灰色理論應用于職災類型的分析與預測[4];Chen et al.應用灰預測理論預測臺灣3G行動電話市場[5];余尚武等應用動量權重及灰預測傅立葉殘差修正模型于臺灣股票市場電子股之投資組合策略[6];Wang使用模糊時間序列與灰色馬可夫修正預測模型來預測觀光需求,證實灰馬可夫修正預測模型能改善GM(1,1)預測模型對于數據隨機波動性較大之缺點[3]。本研究應用GM(1,1)、滾動檢驗、灰色馬可夫以及灰色傅立葉級數殘差修正預測模型來預測埔里酒廠游客量,并對它們進行比較與分析,總結各預測模型對所選擇數據型態的適性,以提供未來游客量評估之參考依據。

2 基地概況

秉承 “文化釀酒、藝術觀光”的傳承與經營理念,埔里酒廠營造 “紹興故鄉”在埔里生根發展,不僅已經是屬于地方的一個活的產業文化,更已成為一個具有酒歷史內容的產業體,且具指標性意義的重點游憩產業。

2.1 區域地理位置

酒廠位處臺灣南投縣埔里鎮內,其位置如圖1、圖2。而埔里鎮位居南投縣北部,東與東北面臨接仁愛鄉,南臨魚池鄉,西與西北面接國姓鄉,以埔里是皆為中心,西距草屯鎮41 km,西北距臺中61 km,東距霧社23 km,南距日月潭17 km,如圖3。

2.2 產業特色

埔里酒廠成立于1902年日據大正年間,其前身為埔里社制酒株式會社,大正11年日人禁止民間制酒,臺灣總督府專賣局于這一年的6月30日接收,改名為埔里出張所,臺灣光復后,埔里酒場由省政府煙酒公賣局管轄,這時的埔里酒廠只生產米酒、太白酒、糯米酒,而且生產不多,后來才改以生產紹興酒為主。埔里酒廠生產的紹興酒,之所以香醇芬芳廣受酒客歡迎,原因之一是拜埔里水質甘良之所賜,酒廠生產酒的水來自愛蘭臺地的泉水,近幾年來埔里酒廠除了積極推出愛蘭白酒、愛蘭喜酒、吟釀清酒等新酒之外,同時還大力推動觀光,設立酒文化館,舉辦酒文化活動,為酒廠的發展找到新的契機,目前酒廠已成為埔里地區最熱門的一個觀光景點。藉由 “產業文化化、文化產業化”的策略,并且結合地方藝文,觀光資源,為國內 “觀光酒廠”經營休閑游憩方向經營成功的案例。

3 研究方法

灰預測理論屬于灰色系統理論的研究內容之一,該理論是由鄧聚龍教授于1982年所提出,主要是針對系統模型之不明確性及信息之不完整性之下,進行關于系統的關聯分析及模型建構,并借著預測及決策的方法來探討及了解系統的情況。并能對事物的不確定性、多變量輸入、離散的數據及數據的不完整性做有效的處理。其中灰預測即是以GM(1,1)模型為基礎,對現有數據所進行預測的預測方法,找出某一數列間各個元素之未來動態狀況,不需要太多數據,且數學基礎較簡單[7]。

3.1 灰預測GM(1,1)模型

灰預測理論的基礎是針對系統過去已發生之數據序列,透過累加生成進行數據處理,以提供建模之中間訊息,弱化原始數列的隨機性,從而發現、揭示潛在的規律,并由規律中預測未來可能的情況[1]。

滾動檢驗 (Rolling Checking)是利用同一序列前面幾個數據 (通常為4筆)來建立GM(1,1)模型,預測下一個數據后,再舍棄原始序列中第1筆數據,加入第5筆數據建立GM(1,1)模型,預測第6筆數據,依此類推的做到原始數據的最后一筆數據為止[7]。由于滾動檢驗法是基于新訊息優于舊訊息的觀點,調整序列發展趨勢的變化度,因此對趨勢發展變化較為強烈的數據更能顯示預測的精確度。

3.2 灰色馬可夫預測模型

灰色馬可夫預測模型M arkov GM(1,1),是由田自力與劉碧發于1996年提出,認為GM(1,1)預測模型適用于數據數據少且符合所謂 “廣義能量系統”的預測,只需少量的數據 (超過4個)即可建立預測模型;但其擬合函數只是一條平滑的指數函數曲線,對于趨勢變動較大的數據擬合較差,預測精確度也較低,故將GM(1,1)預測模型與馬可夫轉移矩陣預測的優點相結合,充分利用歷史數據給予的信息,提高數據隨機波動性較大之預測精確度,且適于長期預測,有效的提升GM(1,1)預測模型對于此類數據的預測精確度[8]。

3.3 灰色傅立葉級數殘差修正預測模型

傅立葉殘差修正方法分為傅立葉級數殘差修正法、傅立葉余弦級數殘差修正法及傅立葉正弦級數殘差修正法,本研究將以GM(1,1)傅立葉級數殘差修正預測模型來預測游客量,透過傅立葉函數適用于周期性系統表達之特性,以改善GM(1,1)預測模型做一次累加生成后的指數函數圖形常會因為社會環境的變遷、循環,而在不同時期有不同的指數率,造成此類大趨勢之周期性數據預測精確度較差。

3.4 殘差檢驗

利用建模所得到的預測數據和原始數據間做殘差比較,以了解實際值和預測值間之誤差及模型精確度。

4 實證研究與分析

由于游客量的變化對于觀光旅游業者之經營管理具有決策性的影響,因此本研究整理統計南投埔里酒廠2008年1月至2009年3月之游客量,如表1所示。首先探討游客量之變化情形,再利用GM(1,1)、滾動檢驗、灰色馬可夫以及灰色傅立葉級數殘差修正方法建立預測模型,對它們進行比較、分析,并預測2009年4月之游客人次。

4.1 游客量變化之探討

由圖4之結果可知,埔里酒廠每月游客量平均在15萬人次以上;而7月、8月暑假期間,學生旅游族群較多時期,游客量突破20萬人次,但相對于9月學生開學時期,其游客量由20萬人次驟降只剩10萬人次,惟至此后游客量均達15萬人次以上,顯見埔里酒廠確實擁有相當高的觀光游憩潛力。

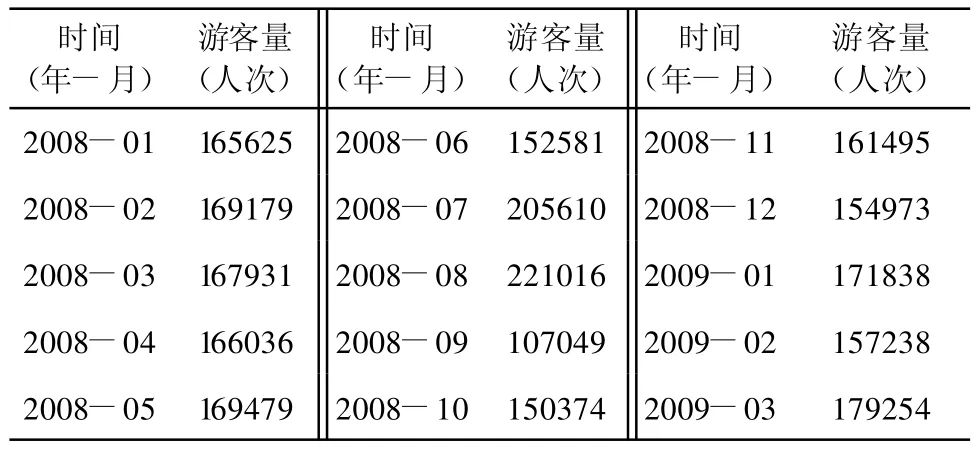
表1 埔里酒廠游客量統計表

4.2 預測結果之探討

在觀光旅游市場中有很多未知的訊息,例如:氣候、景氣、流感疫情等因素,使得觀光旅游地區之游客人次具有不確定性、波動性及周期性等特征,故本研究應用前述研究方法建立預測模型,據以預測游客之數量。

4.2.1 GM(1,1)模式 以南投埔里酒廠統計2008年1月至2009年3月之游客量,建立原始數列(165 625,169 179,167 931,166 036),再由3.1節所介紹之GM(1,1)公式求得預測值 ,其預測結果如表2所示。由表2可知,最大殘差值為48.11%,最小殘差值為 0.06%,平均殘差值為10.50%,最佳模型精確度為99.94%,最差模型精確度為51.89%,平均精確度為89.50%,顯示預測模型預測效果在可接受的水平內。

4.2.2 滾動檢驗 本研究利用滾動檢驗法新訊息優于舊訊息的特性,且對于趨勢發展變化較為強烈的數據有較高的精確度,建立預測模型,即以(165 625,169 179,167 931,166 036)預測2008年5月之游客量;以 (169 179,167 931,166 036,169 479)預測2008年6月之游客量;以(167 931,166 036,169 479,152 581)預測2008年7月之游客量,以此類推的做到原始數據的最后一筆數據為止。由表3預測結果得知,最小殘差值為2.97%,最大殘差值為101.94%,平均殘差值為25.68%。然而,造成2008年9月實際值與預測值間之誤差過大的主要原因,是因滾動檢驗法以新信息取代舊信息,因而無法反應過去舊信息之波動性及周期性之變化,以致無法精確預測游客量,故滾動檢驗法較不適合此類具波動性及周期性數據型態之預測。

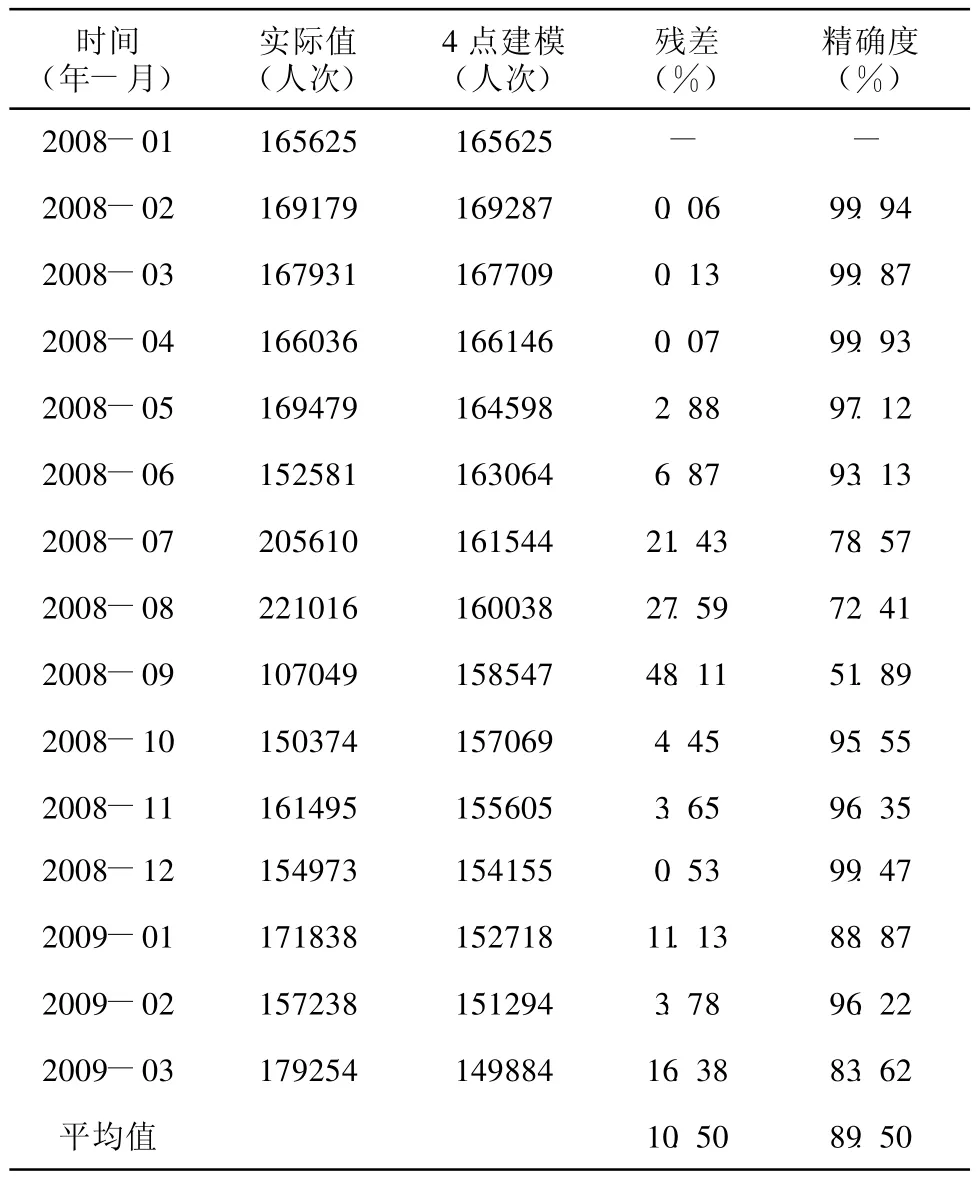
表2 GM(1,1)之預測結果

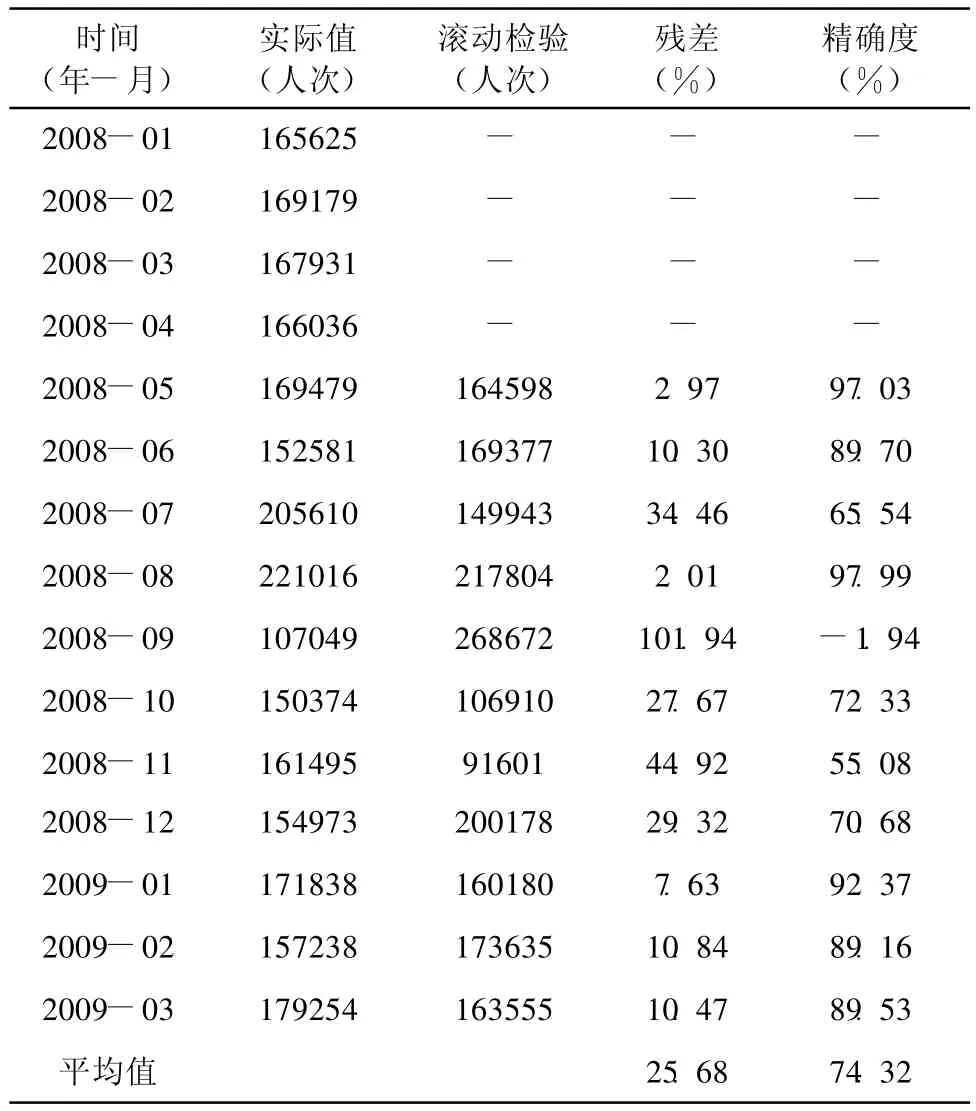
表3 滾動檢驗之預測結果

4.2.3 灰色馬可夫 GM(1,1)預測模型能展現預測序列的發展變化總趨勢,且只需少量數據(4筆以上)即可建模預測;但其擬合函數只是一條平滑的指數函數曲線,對于隨機性較大的數據擬合較差,預測精確度也較低,而馬可夫鏈則適用數據隨機性較大的預測,并可用來確定狀態的轉移概率。在進行灰色馬可夫預測模型時,首先要建立灰預測GM(1,1)模型,再加入馬可夫過程,而輸入變量是依據最小平均殘差值所選出的最適建模點數和狀態參考數據筆數,因而Grey M arkov的所有相關參數設定如表4所示。

表4 灰色馬可夫參數設定表

由Grey Markov預測模式所求得的預測值與實際值間的殘差均明顯偏低,平均殘差值為3.53%,預測模型之平均精確度高達96.47%,顯示預測模型之準確度相當高,如表5所示。

4.2.4 灰色傅立葉級數殘差修正預測模型當GM(1,1)預測模型之原始序列經過累加生成后,會出現明顯的指數規律,但實際系統發展時會受各種因素影響,不可能以某一定速度發展,而是不同時期有不同的指數率發展。因此本研究利用傅立葉函數適用于周期性系統表達之特性,依據GM(1,1)建模方法求出預測值X(0)(j),并將預測值和實際值做殘差比較,得到殘差序列E(j)(108,-222,110,-4 881,104 83,-44 066,-60 978,51 498,6 695,-5 890,-818,-19 120,-5 944,-29370,-53 283),再利用傅立葉級數作殘差修正,得到修正后殘差Ea(j),預測結果如表6所示。由表6得知,最大殘差值為4.29%,最小殘差值為0.58%,其平均精確度高達97.66%。

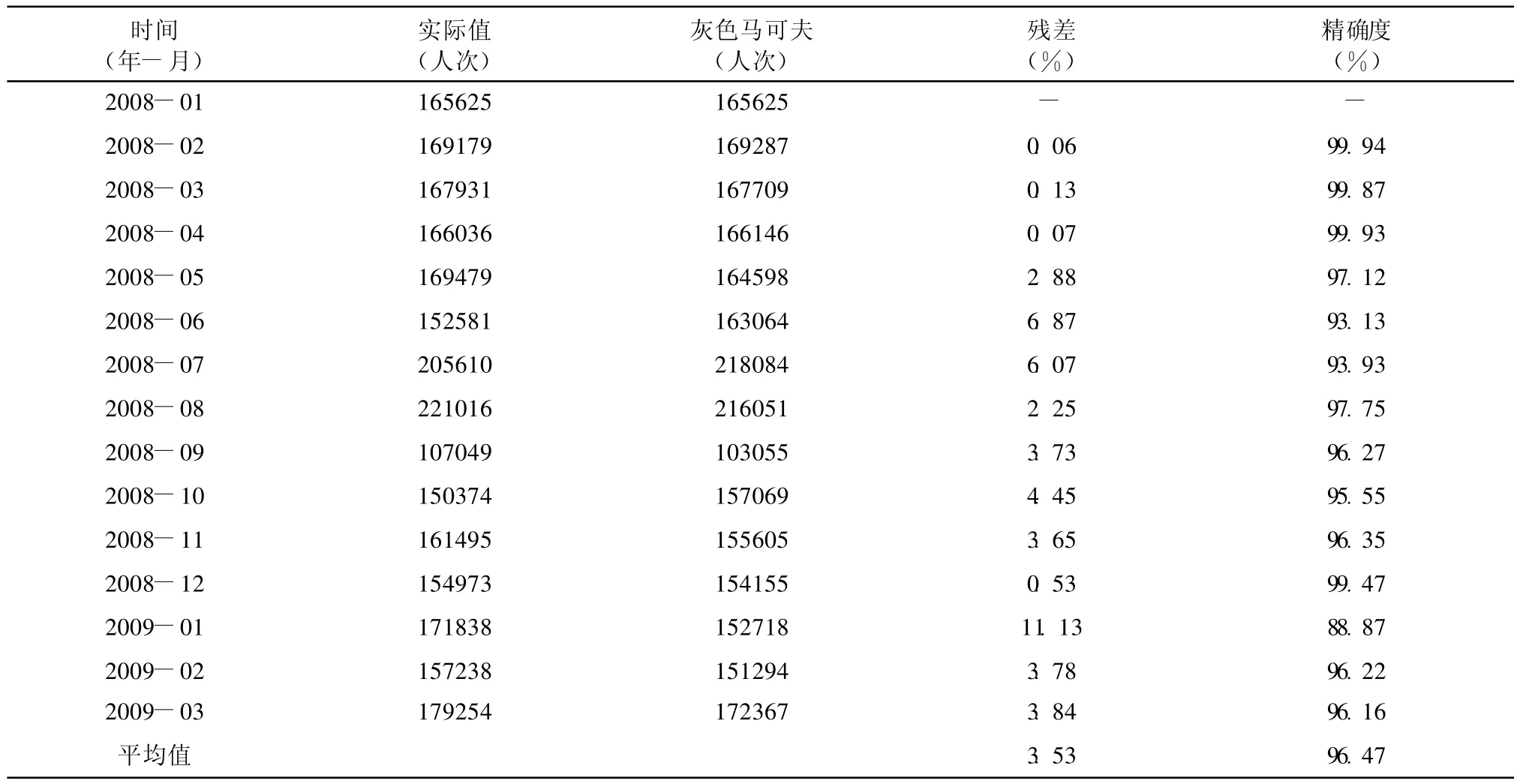
表5 灰色馬可夫之預測結果

4.2.5 各預測模型之比較 由表7及圖4研究結果顯示,滾動檢驗法之預測精度較差,其平均殘差值為25.68%,平均精確度為74.32%。灰色馬可夫及灰色傅立葉級數殘差修正預測模型之預測精確度均高達95%以上,顯見灰色馬可夫及灰色傅立葉級數殘差修正預測模型皆適合此類觀光旅游需求之預測,唯透過此兩種預測模型預測2009年4月游客量與埔里酒廠于2009年5月所公布的游客量統計資料相比時,灰色馬可夫預測之游客量為148 487人次,其殘差值為26.41%,而灰色傅立葉級數殘差修正預測模型之游客量為197 559人次,其殘差值為2.09%,顯然灰色傅立葉級數殘差修正預測模型之預測較為精準,且較灰色馬可夫預測模型更適于此類具波動、周期性質的數據型態之預測。

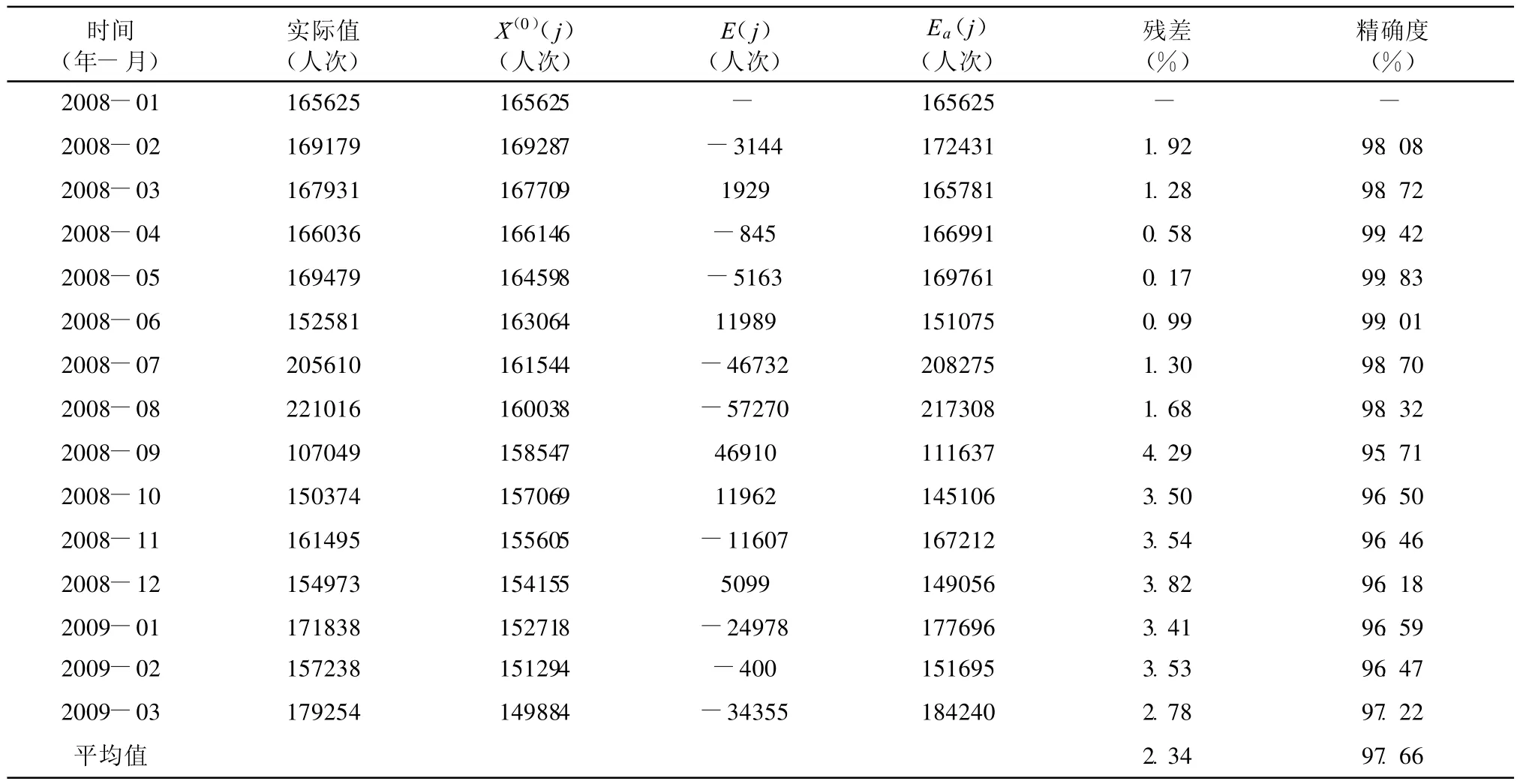
表6 灰色傅立葉預測結果

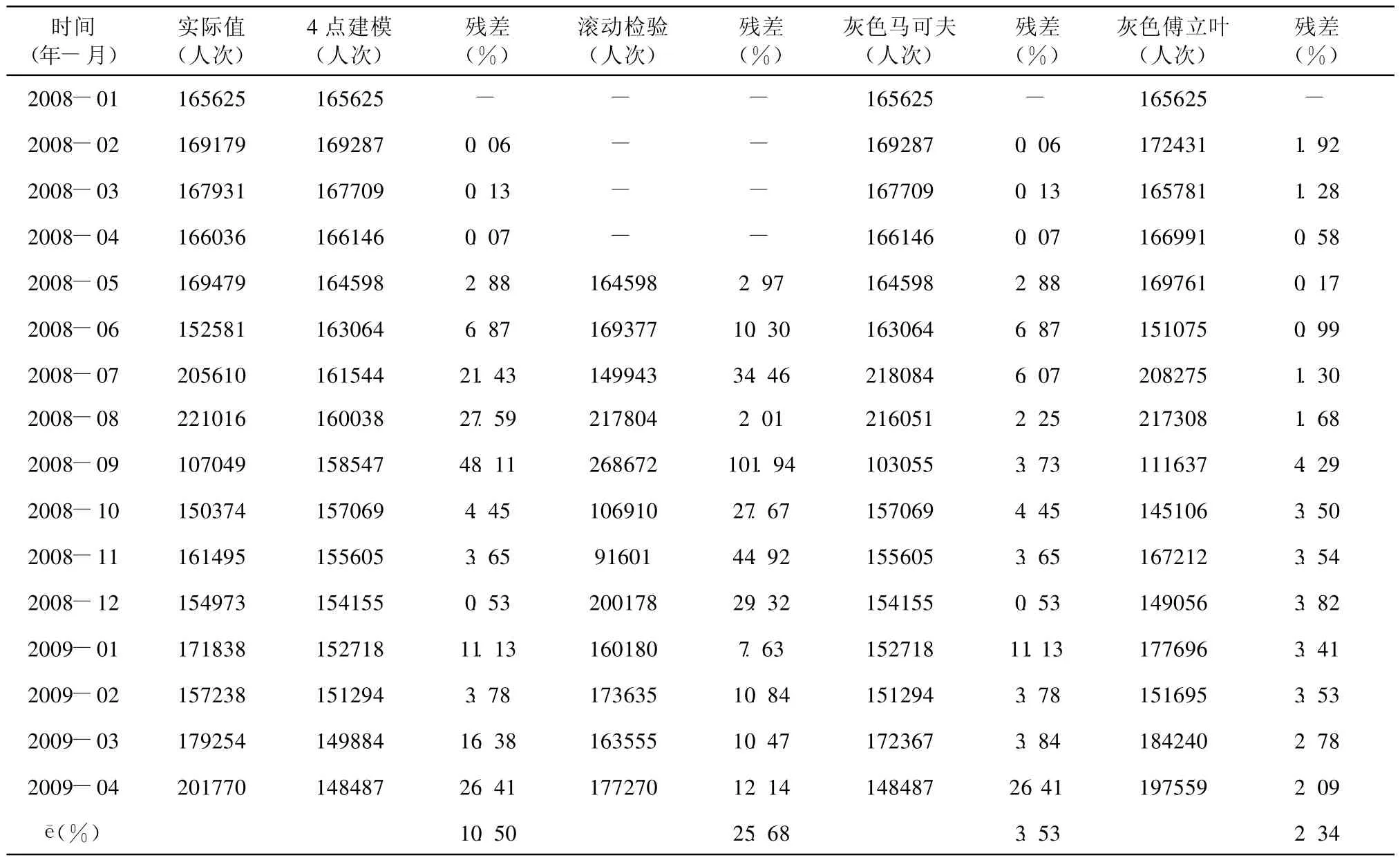
表7 各預測模型之比較及2009-04之預測值

圖4 預測模型之比較

5 結論與建議

以灰預測少量數據的特性,采用GM(1,1)、滾動檢驗、灰色馬可夫以及灰色傅立葉級數殘差修正預測模型建構游客量預測模型,并以2008年1月至2009年3月南投埔里酒廠游客量統計資料為建模樣本進行預測分析。研究結果顯示,灰色馬可夫及灰色傅立葉級數殘差修正預測模型均適合此類觀光旅游需求之預測,其中灰色傅立葉級數殘差修正預測模型之預測精確度高達97.66%,主要是因游客量之趨勢變化受到旅游地點、交通路線、旅游潮流、氣候因素、景氣因素、流感疫情等影響,而具有周期波動的特性,因此使用具周期波動性質的預測模型最為適合。然而馬可夫之長期預測及數據隨機波動較大的特性與傅立葉函數適用于周期性系統表達之特性,恰可以彌補灰色預測的局限。

此外,灰色馬可夫及灰色傅立葉級數殘差修正預測模型皆需使用較多的歷史數據才會有較佳的預測精度,才能反映其長期的整體趨勢及周期性質,進而訂定更精確、更完善的計劃及投資策略,相對必須花費較多數據搜集的時間成本與前置成本。希望本研究建立之埔里酒廠游客量預測模型能提供后續研究者針對相關議題之參考,以及提供相關單位、地方政府與民間企業之相關策劃部門,做為對未來農業休閑觀光需求政策方針之擬訂與觀光市場營銷、營運策略之參考。

[1]高俊雄譯.觀光旅游地區發展[M].臺北︰桂魯有限公司,1998.

[2]黃躍雯,黃亦錫,葉碧華,等.酒類觀光對地方區域發展沖擊之研究 [J].觀光研究學報,2003,10(1):1-19.

[3]Wang C H.Predicting tourism demand using fuzzy time series and hybrid g rey theory[J].Tou rism Managem ent,2004,25(3):367-374.

[4]Hsing C Y,Chang Y C,Yang CC,et al.An assessment of occupational accident impact factors using the grey system[J].Jou rnal of Occupational Safety and Health,2004(14):58-68.

[5]Chen H S,Yan T M,Kung C Y.A pplication of grey prediction theory to forecast 3G mobile phone in Taiw anese market[J].Journal of Grey System,2008,11(1):43-48.

[6]余尚武,盧瑞山,林盈成.應用動量權重及灰預測傅立葉殘差修正模型于臺灣股票市場電子股之投資組合策略[J].電子商務學報,2009,11(1):259-286.

[7]溫坤禮,黃宜豐,陳繁,等.灰預測原理與應用[M].臺北:全華科技圖書公司,2002.

[8]田自力,劉碧發.灰色馬爾可夫鏈預測模型 [C]//臺灣第一屆灰色系統理論與應用研討會.1996:157-161.