噪聲干擾對抗單脈沖末制導雷達技術研究

饒志高，金嘉旺，侯向輝，李仙茂

（海軍工程大學電子工程學院 湖北 武漢 430033）

單脈沖是一種先進的雷達角跟蹤體制。很多反艦導彈末制導雷達都采用這種體制，對此多數干擾技術都難以奏效，對艦艇構成嚴重的威脅。因此，艦艇方須結合自身特點，采用一種有效的防御措施。目前，國外公開發表的有關噪聲干擾對抗單脈沖末制導雷達的研究成果很少見到，國內相關研究也不多，有一些研究表明，噪聲干擾是可以干擾單脈沖雷達的，但沒有明確指出干信比或干擾機功率要達到多大時才能有效干擾。

本文針對此問題做了研究。首先，簡單介紹單脈沖末制導雷達腳跟蹤原理。

1 單脈沖末制導雷達角跟蹤原理

單脈沖末制導雷達就水平方向而言，是在一個角平面內，同時發射兩個相同的波束，使其部分重疊，其交疊方向的中心即為等信號軸。因為兩個波束同時接收回波，故單脈沖測角獲得目標角誤差信息的時間可以很短，理論上講，只要分析一個回波脈沖就可以確定角誤差，所以叫“單脈沖”。單脈沖角跟蹤技術種類很多，最常見的是振幅和差單脈沖技術。這種技術需要兩個或兩個以上的天線才能實現。

圖1為振幅和差單脈沖系統的工作原理框圖，圖中和差信號形成網絡用圓圈表示，它有兩路輸出，其中一路為兩波束輸出信號之和E∑，另一路為兩波束輸出之差EΔ。

若空間目標瞄準軸偏角為θ，則目標回波信號為

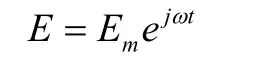
則和、差兩支路輸出分別為

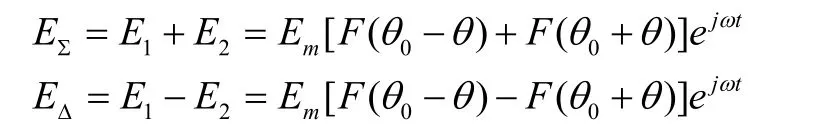
式中，0θ為天線方向圖最大點距等信號軸的偏角。

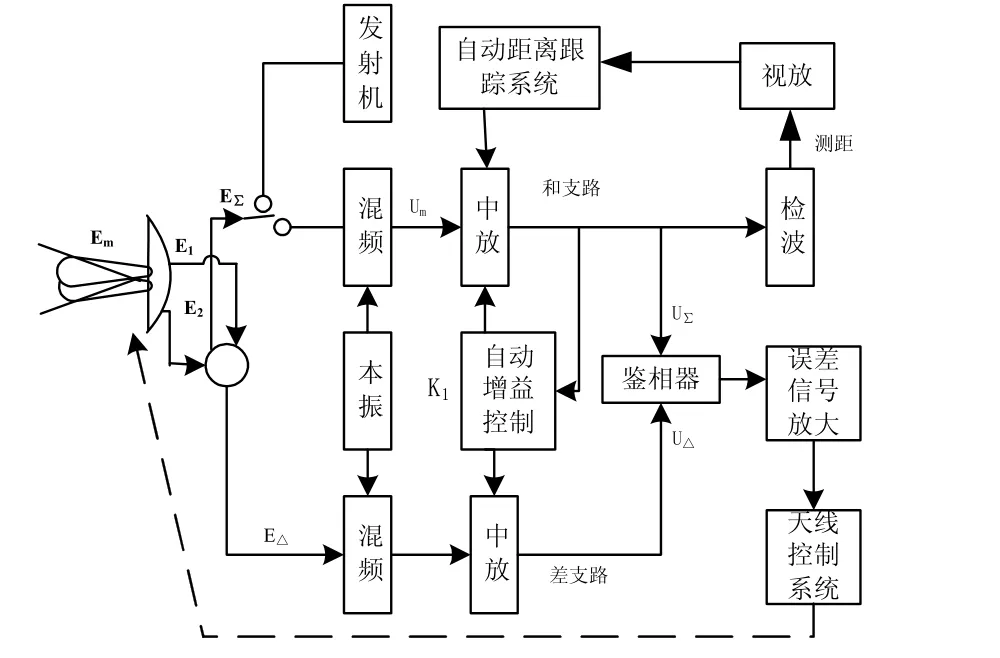
圖1 振幅和差單脈沖系統的工作原理框圖

設和、差兩通道特性相同，即具有相同的相移及放大倍數，則中放輸出信號為

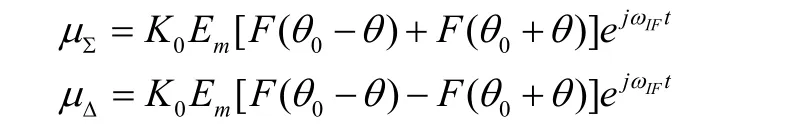
式中，K0為中放放大量，ωIF為中頻頻率。

中放輸出的和、差信號加到相位檢波器的輸出端，相位檢波器完成對和、差相乘并求平均運算，相檢器輸出為

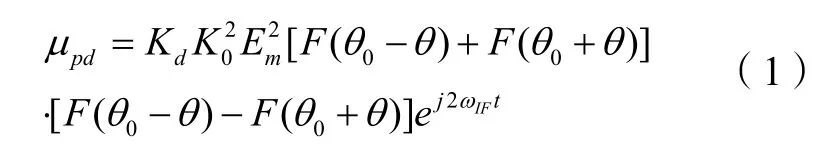
式中，Kd為相檢器傳輸系數。在θ很小時，上式中的 F （θ0± θ）可以近似表示為

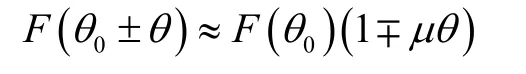
式中，Kpd是式（1）中前面幾項系數的合并。μpd的作用是產生一個力矩，使天線瞄準軸向著目標方向運動，最后，誤差信號為零，達到穩定平衡狀態[2]。

2 噪聲干擾對抗單脈沖末制導雷達

2.1 可行性分析

導彈末制導雷達要捕獲目標，就必須滿足以下條件：

①目標在距離上處在距離搜索范圍之內；

②目標在距離上處在距離搜索波門之內；

③目標在方位上處于末制導雷達水平波束之內；

④目標在方位上處于末制導雷達垂直波束之內；

⑤目標回波強度滿足末制導雷達捕獲門限。

噪聲干擾的主要目的是壓制目標回波信號，阻止或推遲雷達導引頭對目標的截獲，使雷達導引頭難以獲得目標的距離和角度信息，或者增大距離跟蹤的誤差，破壞距離鎖定，最終破壞對目標的跟蹤。噪聲干擾的最佳波形是高斯白噪聲，因為它的熵值最大，最接近導引頭接收系統的內部噪聲，因而導引頭無法區分干擾噪聲和內部噪聲。

依照前述單脈沖角跟蹤的原理，具體分析噪聲干擾對單脈沖角跟蹤系統的影響。由于單脈沖末制導雷達一般采用了頻率捷變體制，可以采用阻塞式噪聲調頻干擾樣式,噪聲調頻干擾的數學模型為

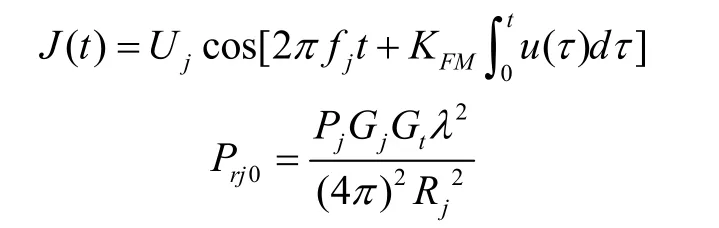
式中，調制噪聲u( t)為零均值、方差為2σ的廣義平穩隨機過程,fj為噪聲調頻信號的中心頻率,KFM為調頻斜率，Rj為導彈到干擾機的距離，Gj為干擾天線增益，Gt為雷達天線增益，λ為干擾機發射電磁波波長，Pj為干擾機發射功率，Prj0為雷達接收機輸入端外的干擾功率。

在實施阻塞式干擾時，進入雷達接收機輸入端內與輸入端外的干擾功率之比為式中，d ｛ ·｝表示兩區間交集的寬度；表示雷達信號工作頻段（捷變頻雷達為變頻范圍）；[fjmin, fjmax]表示阻塞式或掃頻式干擾頻段；Δfr表示雷達接收機帶寬。

1）全數據采集與存儲特點。在大數據理念下，系統平臺的建設支持課題項目的全數據采集與存儲，平臺上數據采集既要包括機構化數據，也要包括以文本、關鍵詞等為代表的非結構化數據。由于教改項目管理非結構化的數據較多且較難分析，而往往這些數據隱含更多的重要信息，因此要著重有利于非結構化數據存儲和分析的系統平臺設計，以全數據采集、統計、分析為特征。

則進入雷達接收機輸入端內的干擾功率為

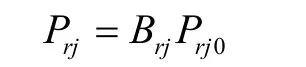
令艦艇偏離瞄準軸θ角，則末制導雷達對艦艇的回波信號為

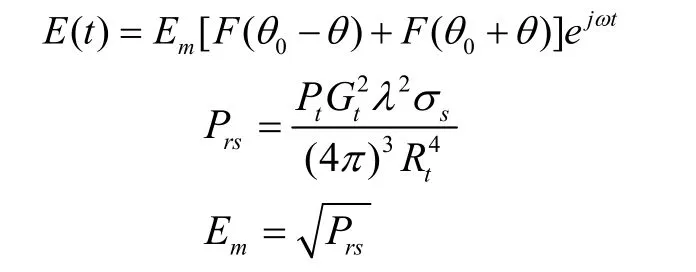
式中，Rt為艦艇到導彈的距離，tP為末制導雷達發射功率，λ為雷達工作波長（近似為干擾波長），Prs為進入雷達接收機的艦艇回波功率，sσ為艦艇的雷達截面積。

由于干擾機是在艦艇上，可近似認為干擾機和艦艇都偏離瞄準軸θ角且 Rj＝Rt，則天線1和2接收的信號分別為

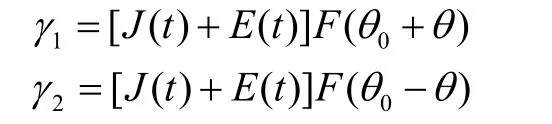
和、差信號分別為

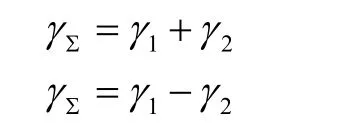
和差信號經過變頻、中放（包括自動增益控制），相位檢波后，得到的角誤差輸出信號為

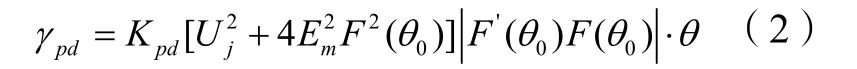
式中，Kpd是與和差支路放大倍數、相位檢波器傳輸系數等有關的常量。假設單脈沖雷達天線為辛克函數型，由于既發射又接收信號，則為雙向工作型，故有

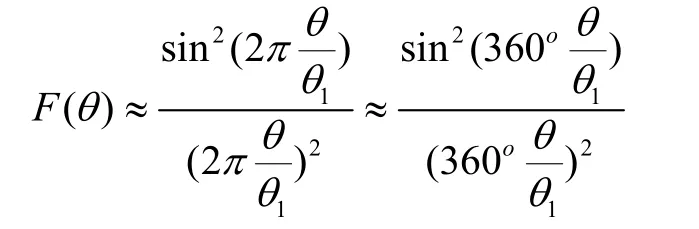
①相位檢波器輸出的角誤差電壓與艦艇偏角大小成正比；

②當 Uj＝ 0 ，即無干擾時，角誤差輸出電壓為

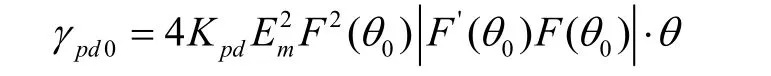
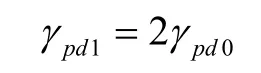
由噪聲干擾信號引起的角誤差輸出平均電壓與由艦艇回波信號引起的角誤差輸出電壓相等；時，角誤差輸出電壓為

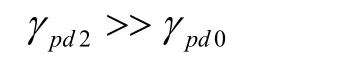
此時，角誤差輸出電壓近似為

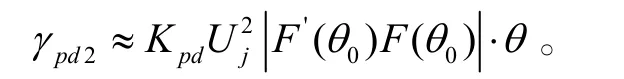
干擾信號可以成功地覆蓋艦艇回波信號，雷達導引頭只能檢測到隨機起伏的噪聲干擾信號。當噪聲起伏干擾而且干擾功率逐漸增大時，將導致自動增益控制電路不能及時響應，角誤差輸出信號也隨機變化并且跳變幅度越來越大，進而使得角跟蹤系統不穩定，最終將遭到破壞而不能進行穩定跟蹤，導引頭將轉為重新搜索狀態。

2.2 噪聲干擾引起的角度跟蹤誤差

為了跟蹤艦艇，反艦導彈末制導雷達需要獲得艦艇準確的角坐標及距離信息。對跟蹤雷達噪聲干擾可以引起角度和距離跟蹤誤差[10]。當噪聲干擾功率較大時，接收機內部噪聲可以忽略不計，此時，對于單脈沖體制的末制導雷達，采用角波門技術測量角度時的標準偏差可表示為[4]：

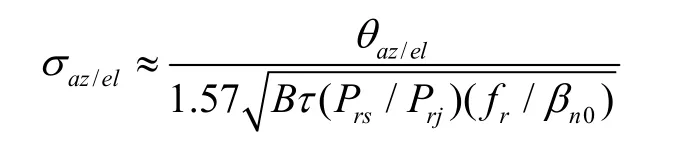
式中，θaz/el為天線在方位或俯仰上的波束寬度，fr為末制導雷達的脈沖重復頻率，βn0為末制導雷達天線最佳伺服系統帶寬，Bτ為接收機等效帶寬和脈沖寬度之積（此處近似為1）。

2.3 噪聲調頻干擾下雷達發現概率的計算

噪聲調頻干擾時，經過單脈沖雷達接收機中放、檢波和n次視頻積累后，輸出電壓u漸近服從正態分布其中，

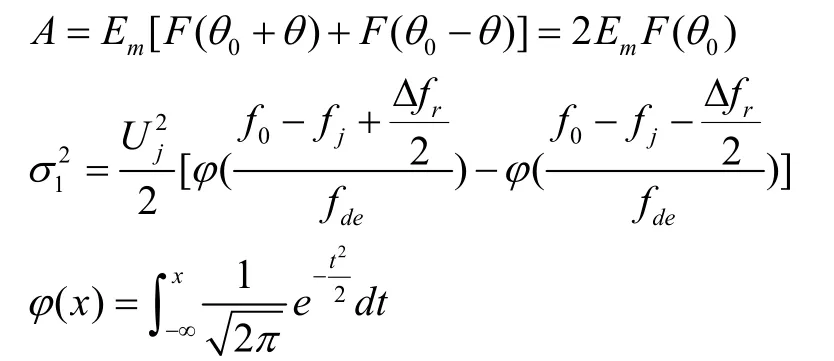
輸出電壓的概率密度函數為

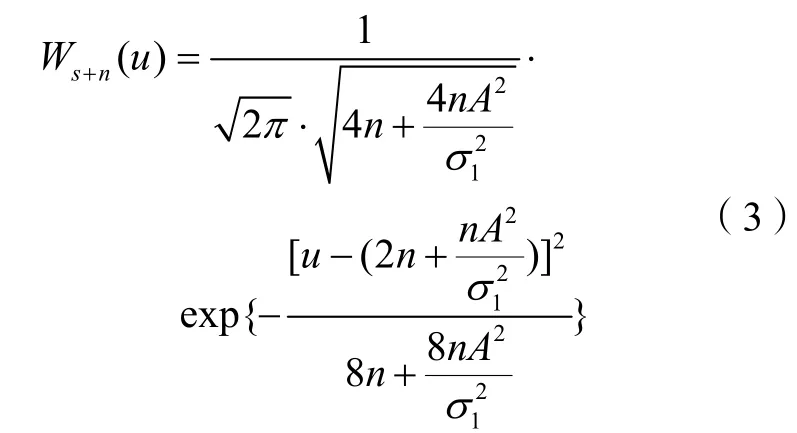
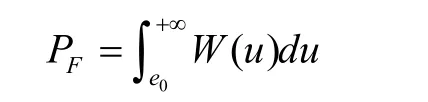
將式（3）代入可得恒虛警門限為

噪聲調頻干擾下，當雷達與艦艇之間沒有相對運動時，雷達對艦艇的發現概率為

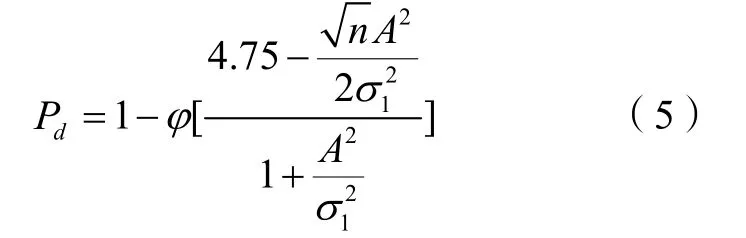
而壓制系數為

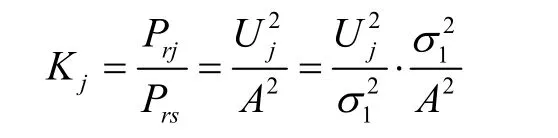
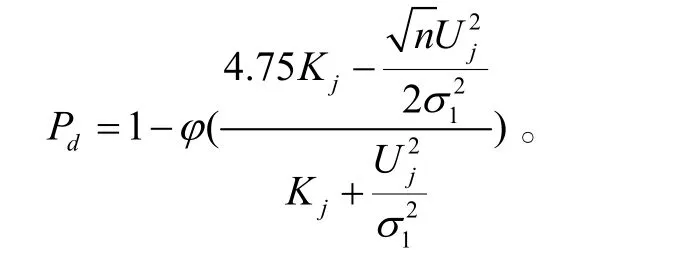
3 仿真驗證

仿真中干擾機的參數為：噪聲調頻信號的中心頻率 fj＝ 1 2GHz ,干擾機阻塞式干擾頻段寬度d[ fjmin, fjmax]＝ 3 00MHz ，干擾天線增益 Gj＝ 2 0dB ；

導彈末制導雷達的參數為：發射信號的中心頻率f0＝ 1 2GHz ，頻率捷變帶寬 Δ f ＝ 2 50MHz，脈沖重復頻率 fr＝ 5 000Hz，雷達天線最佳伺服系統帶寬βn0＝50Hz ，雷達發射功率Pt＝ 4 0kw，雷達天線增益Gt＝ 3 0dB ，雷達接收機帶寬 Δ fr＝ 3 0MHz ，雷達天線在方位上的波束寬度 θaz＝ 5o，天線方向圖最大點距等信號軸的偏角 θ0＝ 2o；

其它參數為：導彈到艦艇的距離 Rt＝ 2 0km ，調頻斜率 KFM＝ 8 × 1 08MHz/V，視頻積累數n＝20，艦艇的雷達截面積 σs＝6000m2。

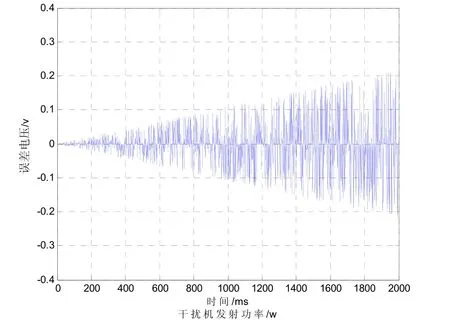
圖2 角誤差輸出電壓隨時間或干擾機發射功率變化關系

圖 2為干擾機發射功率隨時間均勻增長的情況下，角誤差輸出電壓與干擾機發射功率之間的關系圖。可以看出，在剛開始一段時間，由于干擾機功率不是很大，噪聲起伏干擾引起的角誤差輸出電壓的跳變幅度比較小；隨著時間的增長，干擾機功率越來越大，角誤差輸出電壓的跳變幅度也就越來越大。

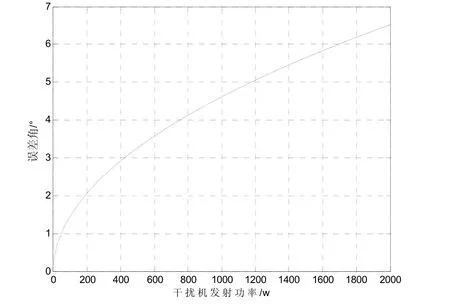
圖3 角度跟蹤誤差隨干擾機發射功率變化的關系

圖3表明了角度跟蹤誤差隨干擾機發射功率變化的關系。根據所設定的參數，由圖3可知，隨著干擾機發射功率的增大，角度跟蹤誤差也呈增大趨勢，這將導致末制導雷達天線擺動角度也越來越大，從而使得導彈的角跟蹤系統不穩定。當干擾機發射功率為400w時，角度跟蹤誤差為天線波束寬度的 60%；當發射功率增大到1200w時，角度跟蹤誤差為天線波束寬度的100%，此時雷達天線實際上已經丟失目標[4]，雷達導引頭將轉為重新搜索狀態。

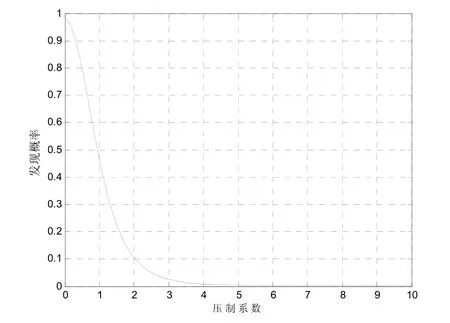
圖4 發現概率與壓制系數的關系

實施噪聲調頻干擾時，發現概率與壓制系數之間的關系如圖4所示。由于普遍采用發現概率 Pd＝0.1作為有效干擾的衡量標準[5]，則根據所設參數并結合圖 4，可以發現，要實施有效的壓制干擾，壓制系數應該不小于2。

理論上分析單脈沖雷達的跟蹤性能時，假定單脈沖雷達接收機對信號是完全對稱的，單脈沖雷達對它的回波信號基本滿足此假設；然而對噪聲干擾信號不滿足此假設。由于強噪聲干擾的影響，使得角度跟蹤誤差加大，超過了雷達的精度要求，因此，強噪聲干擾可以有效干擾單脈沖末制導雷達。

5 結束語

導彈末制導越來越多地采用單脈沖角跟蹤技術，研究艦艇針對單脈沖末制導導彈的對抗技術很有意義。本文從理論上分析了采用自衛式噪聲干擾對裝備有單脈沖末制導雷達的反艦導彈進行干擾對抗，當噪聲起伏干擾時，角誤差輸出信號也隨機變化，從而導致角跟蹤系統不穩定，最終將遭到破壞而不能進行穩定跟蹤，使末制導雷達由跟蹤狀態轉為搜索狀態，從而有效保護已方艦艇。若在末制導雷達的搜索階段結合無源沖淡干擾，則可大大降低艦艇被發現的概率。研究結果對艦載有源干擾裝備對抗反艦導彈末制導雷達有一定的參考價值。

[1]列昂諾夫A N. 單脈沖雷達[M].黃虹,譯.北京:國防工業出版社,1974.

[2]羅景青. 雷達對抗原理[M].北京:解放軍出版社,2003.

[3]丁鷺飛,耿富錄. 雷達原理[M].西安:西安電子科技大學出版社,2002.

[4]張錫祥. 現代雷達對抗技術[M].北京:國防工業出版社,1998.

[5]邵國培,等. 電子對抗作戰效能分析[M].北京:解放軍出版社,1998.

[6]高靜,楊甫,王崳琦,等. 單脈沖雷達導引頭抗噪聲干擾性能分析與驗證[J].航空兵器,2005(5):33-37.

[7]孫富君,陶建鋒,孫宏偉. 單脈沖雷達的角度跟蹤干擾研究[J].現代雷達,2004,(1):17-18.

[8]鞠智芹,吳建忠,董勝波,等. 雷達導引頭在自衛噪聲干擾(SSJ)條件下的抗干擾性能分析[J].宇航計測技術,2003(1):45-50.

[9]I.Kanter.The Effect of Jamming on Monopulse Accuracy[J].IEEE Trans on AES,1979,5(5):738-741.

[10]鄧揚建，安紅.干擾條件下常規雷達效能仿真模型[J].電子對抗技術,1998(1):1-7.

[11]王鑒,張艷花. 單脈沖雷達跟蹤噪聲源性能仿真與分析[J].電子對抗,2005(2):11-14.