CGF智能決策模型中的威脅評估方法研究

李 崢，李照順

（海軍指揮學院，江蘇 南京211800）

高技術海戰中，執行各種作戰任務的水面艦艇面臨著越來越嚴重的空中威脅，對空防御已成為水面艦艇防御的首要任務。對來襲空中目標（主要是指反艦導彈、轟炸機和攻擊機等）的有效防御是建立在及時而準確的威脅判斷基礎之上的，只有對空中目標構成的威脅度作出及時正確的判斷，才能夠合理分配抗擊的兵力兵器，合理確定抗擊的次序，使防御的綜合效益最高。在海戰CGF智能決策系統中，對目標的威脅判斷是行為決策的關鍵任務之一。戰場環境中有很多復雜不確定的因素影響目標的威脅評估。現有包括模糊集理論在內的很多方法用于威脅評估中，能增強行為模型的逼真度。

1 威脅評估方法

威脅判斷受來襲空中目標的性質、類型、攻擊能力以及目標距離、速度和舷角等諸多因素的影響。由于空中態勢復雜多變，使得這些因素都具有不確定性和模糊性。目前，對空中目標威脅判斷常用的層次分析法[1]主觀性太強，而支持向量機[2]（SVM）的方法其核函數選取困難且精度不高，模糊集理論由于在解決不確定性和模糊性問題方面所具有的優越性，而成為威脅判斷研究的良好工具。該方法可以更好地解決CGF智能決策系統中面臨不完整的態勢感知和不確定性信息時的威脅評估問題。

2 威脅因素分析

多個目標產生的威脅等級，實際上取決于多個不同的因素。美國仿真訓練實驗室[3]（IST）對此開展了大量的研究工作：一些與戰場態勢相關，如天氣情況、地理環境、敵、我、友軍隊的兵力部署及戰斗力等，還有一些涉及到所分析目標的特征，如編隊信息、射擊狀態等。在CGF行為決策模型中，進行威脅估計通常考慮的因素主要有：聚合級威脅評估、近程防御、目標的有效射程、目標的射擊狀態、視線角、目標的相對高程、目標的機動、目標類型、射擊扇面等[4]。

2.1 聚合級威脅評估

隨著分布交互仿真規模的不斷擴大，平臺級實體越來越無法滿足要求。將一定規模的作戰實體聚合起來，通過對聚合級實體的作戰行為進行足夠的建模，將有效地解決平臺級實體仿真中出現的規模小、模型復雜、網絡負載大等問題。聚合級實體中的目標，若屬于一個具有威脅的聚合級實體則其威脅度更高。因此，主要考慮以下威脅因素：

1）編隊類型信息。由于不同類型編隊的武器裝備和艦艇平臺性能是不同的，目標的攻擊方式、攻擊威力等都不同，因此，其威脅度也不相同。

2）目標距離。由于火力打擊距離有限，目標距離也是影響打擊決心的因素之一；同時，目標愈近，相對威脅度也愈大；所以應優選距離較近、在火力打擊范圍之內的目標。

3）目標航向。通過對目標航向的觀察，可大致推測海上目標之意圖。敵奔我而來，則敵進攻意圖明顯；敵背我而去，則敵逃跑意圖明顯。由此可見，目標航向不同，對指揮員決定打擊決心的影響亦不同。

4）目標航速。航速是衡量目標機動性能的重要指標之一，也是目標重要屬性之一。不同的目標具有不同的作戰速度，即使是同一海上目標，速度不同，其威脅度也有所不同。一般認為，目標的速度越快，其威脅度越大。

5）瞄準狀態。指目標武器系統的攻擊狀態，即是否正確瞄準所要打擊的目標。

6）機動性。目標抗機動能力越強，越能影響對目標實施打擊的火力，對目標殺傷概率及戰果也會相應下降，相應威脅度也增大。目標的機動性能大大提高了其突防能力和命中概率。

7）鎖定目標概率，取決于裝備在目標上的電子戰探測設備效能。

2.2 近程防御

如果當前戰場態勢中存在能同樣打擊目標的友方實體，那么目標的威脅等級就會降低，但要保證始終大于0。

2.3 目標的有效射程

如果平臺在目標的火力打擊范圍內，那么其威脅等級會增加。為模擬出這種武器的射程，根據該武器的有效射程和最大射程建立一組和威脅等級相對應的四個射程范圍，分別定義為：最小范圍、邊界范圍、殺傷范圍和致命范圍。

2.4 目標的射擊狀態

目標的狀態直接影響其威脅等級。涉及這一因素的主要有四個子因素：

1) 目標正處在開火狀態；

2) 目標正瞄準平臺；

3) 目標已經射擊完畢；

4) 目標正在處于搜索階段。

2.5 視線角

這一因素表示了飛行器的跟蹤方向，只有飛行器要考慮這一因素。如果目標躍升攻擊將增加目標的威脅等級。

2.6 目標的相對高程

作戰想定中海拔的高低可能會影響威脅等級。表示這一因素的模糊集的值為：低于海平面、高于海平面、遠遠高于海平面。

2.7 目標的機動

這一動態因素能預測出駛向平臺的目標是否變得更具威脅。

2.8 目標類型

目標類型直接影響威脅等級。然而為此，目標類型需要提前定義。如果目標類型不能確定，那么就必須用其它方式預測出它的類型或者為了保險起見將默認的威脅等級設置為最高。

2.9 射擊扇面

作戰單元搜索目標的掃描扇區稱為射擊扇面。如果平臺在射擊扇面內，那么目標的威脅等級將會增加。

3 威脅等級的計算

在測量和評估以上因素時考慮到固有的不確定性和模糊性，可以利用模糊集理論[5]來表示。

3.1 集合的定義

設 X，Y是兩個有限集，X表示影響威脅度 Th的因素集，由以上分析的威脅因素構成。Y表示威脅度的有限集合。對定性的屬性采用G.A.Miller的9級量化理論進行量化，并進行歸一化處理；對定量屬性采用區間量化，并對其進行歸一化處理。定性屬性的量化值和定量屬性的量化區間通常要通過專家群組決策來確定。例如，Y = {0, 0.1, 0.2, 0.3, 0.4, 0.5, 0.6,0.7,0.8, 0.9, 1}分別表示威脅程度極小、非常小、較小、小、中大、較大、非常大、極大。R表示X到Y的模糊關系。模糊關系R通常用區間[0,1]中的系數構成的矩陣表示，R(x,y)表示有序對(x,y)具有關系R的程度。

設A和Th分別表示X和Y的模糊關系函數。定義運算符?，對所有的y∈Y，有：

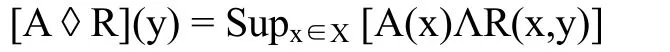
注意到A?R是Y的模糊子集。此外，由對運算符?的定義可知，[A?R](y)表示著Th等于y。根據Sup-min運算并且在圖1中可以直觀地看出來。如圖1所示，y與A之間鏈路的權重等于最小鏈路的模糊關系值（min運算）。y與A之間的關系隸屬度等于所有鏈路權重中最大的鏈路權重值（Sup運算）。因此，對于所有的y∈Y，Th(y)= [A?R](y)，簡化記為：

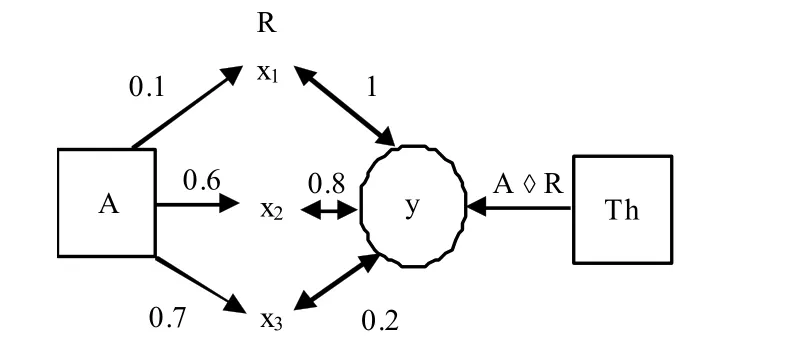
圖1 ?運算圖釋

針對一個目標，給出模糊關系R和對應隸屬度A的集合，方程(1)可以計算出威脅度Th。反過來，給定某一目標的威脅度和隸屬度A的集合，解方程可以得出R。方程(1)的解可能不唯一，即給定一組A和Th，不只一種關系集合滿足方程。然而滿足方程(1)的最大模糊關系集被定義[6]為：

這里，φ是定義在[0,1]的模糊蘊涵運算符：

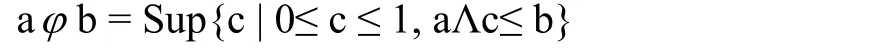
通過方程（2）可以得到A和Th之間滿足方程（1）的最大模糊關系集關系集R也能作為A和Th之間模糊推理集。

3.2 估計最大的模糊關系集

對于給定目標的隸屬度A的集合和A與Th之間的模糊關系R，建立了計算威脅度Th的方程（方程（1））。由方程（2）就可以得到A和Th之間滿足方程（1）的最大模糊關系集。為了能得到模糊關系R，從而給定目標屬性值就能計算或估計出它的威脅度，需要在某一屬性集與Th值之間建立對應關系。這一估計問題可以描述為：

對于一組模糊集合對(A1,Th1),……,（AN,ThN），估計出R使得方程對所有的K=1,2,…,N，都滿足：

給定的集合對看作訓練集合，根據它估計出關系集R。如果設計適當的訓練集合，就可以由給定的目標屬性集合A估計出任意目標的威脅度。

方程（3）中每個獨立的方程對應方程（2）最大的解可能不只一種。令?k為滿足第K個方程的關系集：

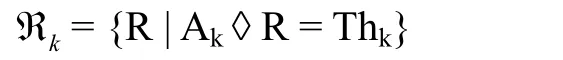
如果：

通過把所有滿足各個獨立方程的最大模糊關系相交，可以算出滿足方程的最大的解，即

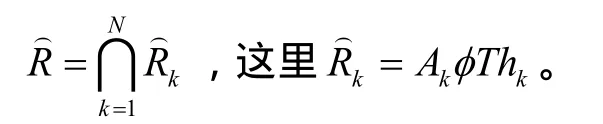
由實踐得知：判斷條件（4）通常比較困難，因此常采取以下步驟估計出關系集R。

3.3 算例分析

為了舉例說明上述算法，簡化起見，對X,Y做如下定義：

其中，X表示影響Th的屬性，包括如下屬性：聚合級威脅評估（ATA）、近程防御（NCT）、目標的有效射程（TER）、目標的射擊狀態（TFS）。Y表示威脅度集合，分別表示威脅程度極小、較小、小、較大、非常大、極大。

用向量矩陣表示模糊集A和Th，按集合X,Y的順序隱含表示。如A = {0.9/ATA, 0.1/NCT, 0.8/TER,0.4/TFS}，可記作A = [0.9, 0.1, 0.8, 0.4]。為了簡化說明，設訓練集合由如下兩組模糊集組成：

由方程(1)得：

同理得到：

交叉相乘得：

例如,

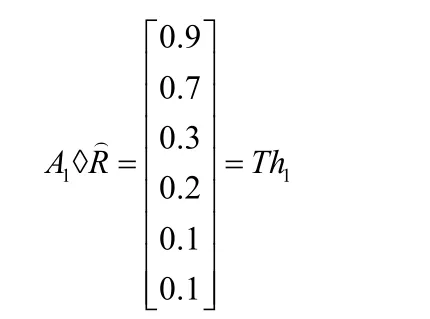
3.4 估算最大的模糊關系

基于上述算法的大量試驗表明，在很多情況下，步驟2)算法中得到的最大關系集不能滿足方程，但得到的Th的值與訓練集中的初始值很接近。在一些情況下，如果由關系值得到的Th值在由訓練集提供的初始值的范圍內，近似解也是可以接受的。用ε表示由Th決定的關系值允許的誤差范圍。在步驟3)算法的基礎上擴展，由給定的訓練集可以得到一個近似解。

3) 如果(distance(Thk, [Ak?R])≤ε)對所有的k=1,2,3,…N都成立，那么是近似解。

4 結束語

本文對CGF智能決策模型中目標的威脅因素進行了具體分析，闡述了利用模糊關系方程算法進行威脅評估，并通過實例計算給出了實踐中估算最大模糊關系的方法。例如，美國Loral公司為SIMNET開發的ModSAF計算機生成兵力系統[7]就利用了這種算法建立了威脅等級和影響因素之間的模糊關系，并以此通過給定的影響因素估計出目標的威脅等級。結果表明，該方法能滿足CGF決策模型的需求，增強了CGF仿真系統的精度和逼真度。

[1]宋國春,劉忠,黃金才.AHP方法的敵地域通信網通信鏈路威脅評估[J].火力與指揮控制,2008,33(2):16-20.

[2]黃現江,余思明.基于修正核函數的支持向量機空襲目標威脅評估[J].指揮控制與仿真,2009,31(6):33-35.

[3]郭齊勝.計算機生成兵力導論[M].北京:國防工業出版社,2006.

[4]葛恩順,包磊.基于模糊理論海上目標威脅評估的改進算法[J].艦船電子對抗，2009,31(6):44-47.

[5]劉林.應用模糊數學[M].西安：陜西科學技術出版社,2008.

[6]Pedrycz W..Gomide fd.An Introduction to Fuzzy Sets Analysis and Design[M].MIT Press, Cambridge,Massachusetts, 1998.

[7]龐國峰.分布式虛擬戰場環境中計算機生成兵力系統的研究[D].北京:北京航天航空大學,2000:6-9.