理解量子效應的新視角*

居學海

(南京理工大學化學系 江蘇南京210094)

參考文獻

理解量子效應的新視角*

居學海

(南京理工大學化學系 江蘇南京210094)

以一維勢箱中的粒子為例，從直觀的視角對量子效應及其之間的關聯做了闡明。作為討論一維勢箱量子效應的補充材料，有助于學生進一步理解微觀粒子基本特征。

一維勢箱中的粒子作為最簡單的微觀粒子波動模型，通過求解類波動方程，求得能級和波函數。并由此得出微觀粒子的最基本特征——量子效應，即能量量子化、零點能效應、沒有經典運動軌道只有概率分布。為了更深刻理解量子效應，作者在教科書通常解釋的基礎上作如下延伸。

1 零點能效應是能量量子化的必然結果

由Ei=kE0(k是正整數。對一維勢箱，k=n2，n=1，2，3…)可知，若E0=0，則Ei=0，即不存在能級差。這與能量量子化相矛盾。能量量子化決定了零點能效應的存在。

2 零點能效應是波函數存在的必然結果

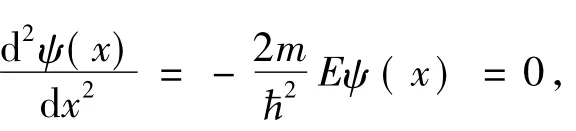
3 沒有經典運動軌道是微觀粒子的非連續運動結果

微觀粒子沒有經典運動軌道(只有概率分布)，體現了微觀粒子的非連續運動。因此，ψ不是粒子運動軌道，沒有明確物理意義，只有其平方才代表粒子出現的概率。認識了微觀粒子的非連續運動，才能理解波函數存在節點(當n≥2時)。非連續運動也表現在描述其狀態函數是一系列正交函數的完備集合，而不是經典運動軌道中的單個運動方程。正是這種非連續運動導致了原子系統分立能級(即量子躍遷)的存在;也正是這種非連續運動導致了微觀粒子的波粒二象性。所有的量子困惑都起源于這種非連續運動。初學量子力學覺得難以理解甚至不可理喻，這并不奇怪，因為人們生活在經典世界中，所看到和經歷的都是經典物體和它們的連續運動。然而，這一切對于量子世界中的粒子和運動都不再適用。我們熟悉的連續運動只是非連續運動的一種特殊的理想化形式。

4 關于n取負整數

由邊界條件得sin((2mE)1/2?－1l)=0，即(2mE)1/2?－1l=±nπ，n=1，2，3，…。但類似的邊界條件在討論角動量z方向分量時得eiα=cosα+i sinα=1，即α=2πm，m=0，±1，±2…。為何一維勢箱中不用(2mE)1/2?－1l=nπ，n=±1，±2…來表述?學生往往會問n可取負整數嗎?

5 關于自由粒子

可以在空間任何位置出現，即當x=±∞時，ψ≠0。顯然，一個非零函數的平方在無限空間積分是不收斂的。這與函數ψ2從－∞積分到+∞的積分值等于1相矛盾。所以完全自由的粒子實際上是不存在的。

6 量子效應向經典力學過渡

7 ψ正交化簡單圖示

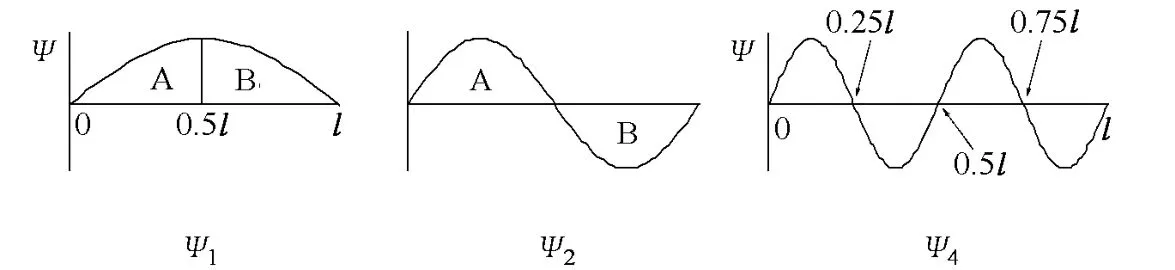
圖1 ψ示意圖

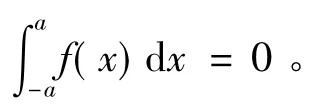
參考文獻

［1］ 周公度，段連運.結構化學基礎.第3版.北京:北京大學出版社，2002

［2］ Levine Ira N.Quantum Chemistry.5th ed.New Jersey:Prentice Hall，Inc.2000

［3］ 徐光憲，黎樂民，王德民.量子化學——基本原理和從頭計算法.第2版.北京:科學出版社，2007

南京理工大學研究生精品課程建設項目