量子理論中一個定理的隨機推廣

歐謙寧

(鎮江機電高等職業技術學校,江蘇鎮江212016)

1 引言

量子化問題起源于信息理論和工程技術,歷史可以追溯到20世紀40年代[1].最早最熟悉的有量子頻標,半導體(包括你正在用來讀這些文字的電腦、手機等),激光,核反應,甚至一般研究用的一些技術(算半個工程吧)像光譜分析,核磁共振,也包括順磁共振,還有探針顯微術系列(STM(掃描隧道顯微鏡),AFM(原子力顯微鏡)等).還有上屆的諾貝爾獎、用在磁盤上的巨磁電阻效應,CPU就是典型的應用.另外量子信息(包括量子計算和量子通信)也在研究當中.

Graf和Luschgy系統地研究了這個問題并給出了具體的數學處理方法.由于自然現象的變化多端和不確定性,因此對隨機性的研究將具有更廣泛的實際意義.隨著近幾年隨機分形研究的興起,隨機情況下量子理論也得到了廣泛重視.主要研究量子理論中的一個定理在隨機情況下也成立,這將進一步豐富量子理論.

2 基本概念

量子化理論的兩個重要內容是量子化系數和量子化維數.

設μ是Rd上的一概率測度,0＜r＜∞,μ的r級n維量子誤差定義為

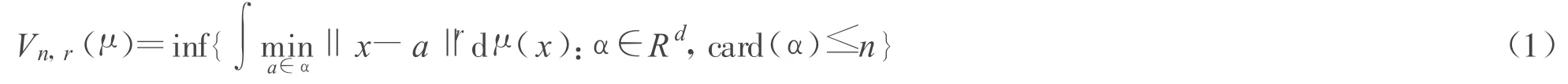
(card表示集合的基數)

如果式(1)中的最小值在某一確定的α∈Rd且card(α)≤n處取得,則稱α為一個μ的r級n維量子誤差的最優集.所有這些最優集組成的集類記作Cn,r(μ).μ的r級n維量子誤差的上、下量子化維數定義為：

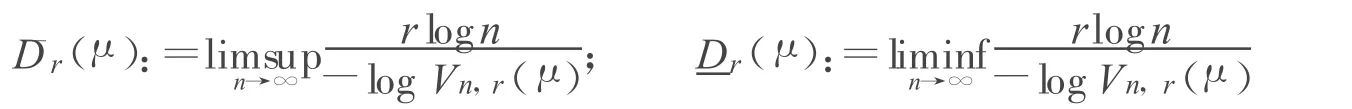
設{f1,…,fN}是Rd上壓縮比為c1,…,cN的一列迭代相似函數系統,E為相應的唯一非空不變集,滿足E.與迭代函數系{f1,…,fN}和給定概率(p1,…,pN)相關聯的自相似測度 μ滿足.稱{f1,…,fN}滿足強分離條件(SSC)：如果 fi(E),1≤i≤N 兩兩不交.稱{f1,…,fN}滿足開集條件(OSC)：如果存在一非空開集U 使得對所有i=1,2,…,N有fi(U)?U,且對任意 i,j,1≤i≠j≤N,fi(U)∩fj(U)=φ.在開集條件下Graf和Luschgy[2,3]證明了 μ的量化維數存在且等于Dr.其中Dr為下面方程的解：

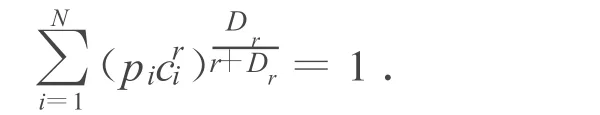
設(Ω,F,P)是一完備的概率空間,N是為一自然數且N≥2.設 Ξ：={1,2,…,N}是一指標集,Ξk：={(i1,i2,…,ik)：ij∈ Ξ,1≤j≤k},

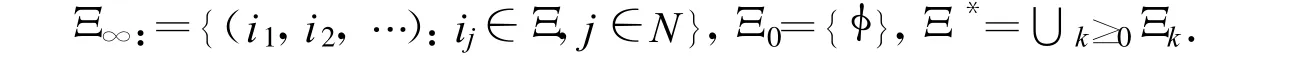
σ=(σ1,…,σk)∈ Ξk,稱 σ的長度為k,記作|σ|=k.對任意 σ∈ Ξ*∪ Ξ∞且|σ|≥k,記 σ|k=(σ1,…,σk).如果 σ,τ∈ Ξ*且|σ|≤|τ|,σ=τ||σ|則稱 σ為τ的前綴,記作 σ?τ.如果既不是 σ?τ也不是 τ?σ,則稱 σ,τ不可比較.一個有限集Γ?Ξ*稱為有限對抗鏈,如果有Γ中任兩個指標σ,τ都不可比較.一個有限對抗鏈Γ稱為最大有限對抗鏈,如果對任一指標 σ∈ Ξ∞在 Γ中都有前綴.對 k≥2,σ=(σ1,…,σk)∈ Ξk,i∈ Ξ,定義

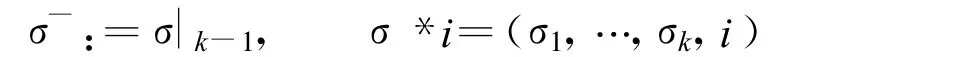
定義 1[4,5]： 設{f1,f2,…,fN}?con(Ω,E),K(ω,ω1,…,ωN)∈ M(ΩN+1,K(ε))稱 K(ω,ω1,…,ωN)是一隨機自相似集(R.S.S.S.)：若存在一個集合 Ω0,p(Ω0)=1使得對所有(ω,ω1,…,ωN)∈ Ω有K(ω,ω1,…,ωN)=表示壓縮映射集)

一般記 K(ω,ω1,…,ωN)=K(ω)

設

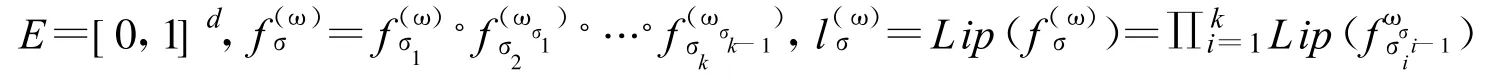
Eσ=fσ(E).EN+1為 PN+1的期望算子 .

與概率向量(p1,p2,…,pN)關聯的隨機自相似測度μ定義如下：

{

f1,f2,…,fN}?con(Ω,E)是Rd到Rd上的壓縮因子為Lip(fi)(i∈Ξ)的相似映射.其分布為(p1,p2,…,pN)

則

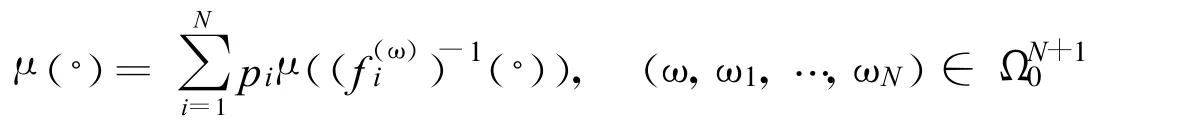
則K(ω)=suppμ是(f1,f2,…,fN)的吸引子.(supp為測度的支撐)

在文中,給出下面的定義和符號.對于 σ∈ Ξk,記顯然序列是單調的.所以當k→∞時以概率1收斂到隨機變量且有

設(A)ε為集A的ε一領域.由SSC,存在一常數 β＞0使得對任一 σ∈ Ξk,有

對于 α∈Cm,r(μ)和 σ∈Γn,定義

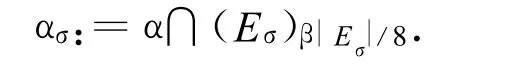
3 主要結論

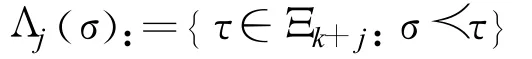
則由三角不等式得：

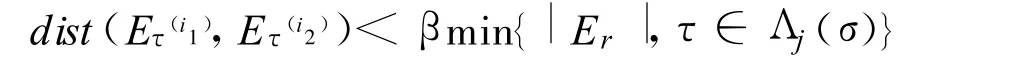
這與式(3)矛盾.因此,對每個 a∈ α,最多只有一個柱集 Eτ,τ∈ Λj(σ)使得式(4)成立.另一方面,由因此,存在某些使得

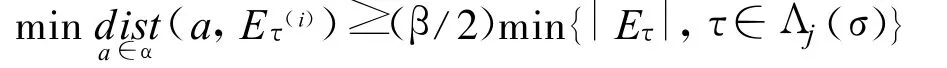
所以,得到

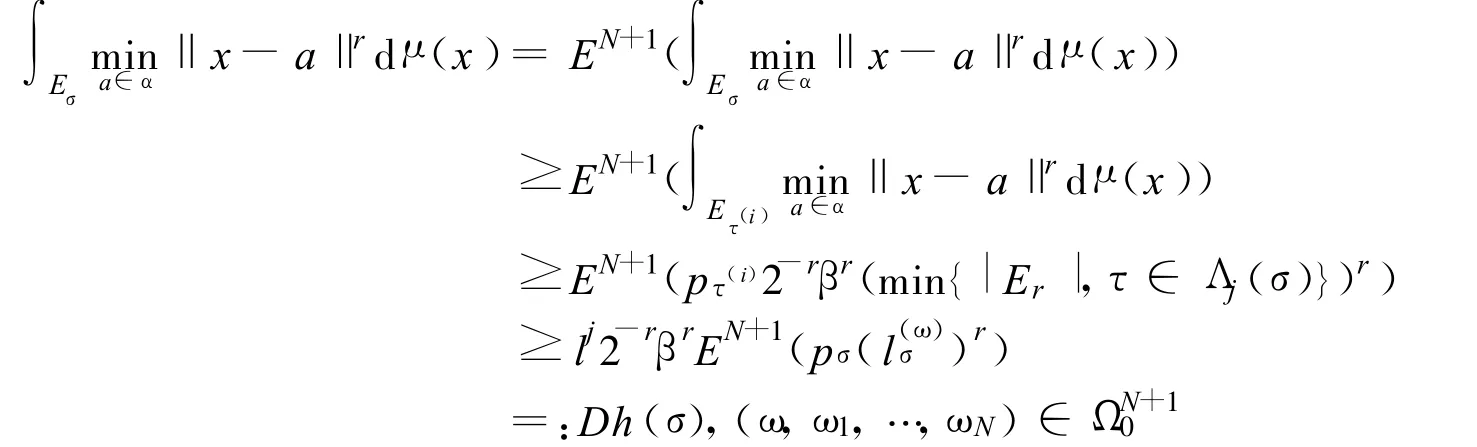
這里 D=lj2-rβr. 定理成立.

[1]J A Bucklew,G L Wise.Multidimensional asymptotic quantization with rth power distortion measures[J].IEEE T rans.Inform.Theory,1982,28：239-247.

[2]S Graf,H Luschgy.The quantization dimension of self-similar probabilities[J].Math.Nachr.,2002,241：103-109.

[3]S Graf,H Luschgy.The quantization of the Cantor distribution[J].Math.Nachr.,1997,183：113-133.

[4]D H Hu,X M Zhang.The random shift set and random sub-self-similar set[J].Acta Mathematica Sci-entia,2007,(2)：267-273.

[5]D H Hu,X M Zhang.The Dimension for random sub-Self-Similar set[J].Acta Mathematica Scientia,2007,(3)：561-573.