集值映射迭代根的不存在性

李春曄

(嘉興學院數學與信息工程學院,浙江嘉興314001)

1 引言

給定一個映射 f：X→X,其中X是一個非空集合,如果存在映射g：X→X,滿足以下方程

則稱g為f的n次迭代根。

自從Babbage在1815年研究恒同映射的迭代根問題[1],越來越多的人開始關注方程(1)的各種形式解[2-5]。至今,關于區間上嚴格單調自映射的結果相對豐富一些[3,4]。簡單地說,區間上嚴格遞增的連續自映射具有任意次連續遞增根,同時也存在任意偶數次連續遞減根。而嚴格遞減映射卻沒有偶數次連續根。對于非單調的情況,文獻[6-8]研究的是一類嚴格逐段單調連續函數,簡稱為PM函數,通過特征區間來刻畫其迭代根的構造。

除了連續函數的迭代根,同樣關注非連續的情況,而集值映射便是其中一種。文獻[10]在文獻[3]的基礎上,繼續研究此類映射的不存在性問題,并且討論一類嚴格遞增且上半連續的集值映射,給出其兩次根的具體構造。研究的是具有兩個集值點的映射,給出此類映射兩次迭代根不存在的條件。

2 主要結果

令I=[a,b]是一給定區間,當 x1,x2∈I且x1＜x2,稱集值映射 f：I→2I是嚴格遞增[嚴格遞減]。如果supf(x1)＜inf f(x2)[inf f(x1)＞supf(x2)],不管是嚴格遞增還是嚴格遞減,統稱為嚴格單調。

給定c1,c2∈I,令F(I)[F1(I),F2(I)]分別代表所有嚴格單調的集值映射 f：I→2I滿足基數#f(ci)＞1[#f(c1)＞1,#f(c2)＞1],并且對任意 x∈I{ci}[x∈I{c1},x∈I{c2}],f(x)是個單值,其中 i=1,2。引理1 令 f∈F(I),那么 f的所有兩次迭代根都屬于集合F1(I)∪F2(I)∪F(I)。

證 令g：I→2I是f的一個兩次迭代根。根據 f的單調性,g也是一個嚴格單調的集值映射。若存在 x0∈X{ci},滿足#g(x0)＞1。不妨令 u,v∈g(x0),那么 g(u),g(v)∈g(g(x0))=f(x0)。由于 f(x0)是個單值,這就意味著 g(u)=g(v),則 u=v,那么#g(x0)=1,因此 g∈F1(I)∪F2(I)∪F(I)。

定理1 令 f∈F(I),如果 f(ci)={ci,xi},xi∈I,i=1,2,那么 f不存在兩次迭代根。

證 反證法,假設 f存在兩次迭代根g：I→2I。根據引理1,g∈F1(I)∪F2(I)∪F(I)。若#g(c1)＞1[#g(c2)＞1的情況可以類似討論]。由已知條件c1∈f(c1)=g(g(c1)),則存在 p1∈g(c1)滿足 c1∈g(p1),那么 g(c1)?g(g(p1))=f(p1)。因為#g(c1)＞1,這就意味著 p1=c1或者 p1=c2。

若 p1=c1,即 c1∈g(c1),則

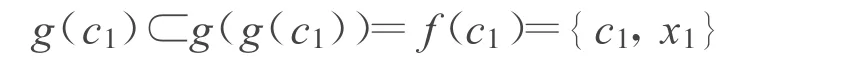
于是有 g(c1)={c1,x1},并且

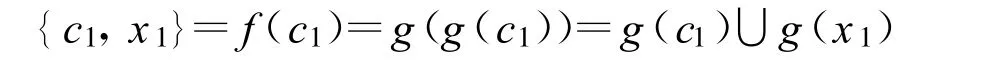
則 g(c1)∩g(x1)≠?,與 g的嚴格單調性矛盾。因此有 p1=c2,即 c2∈g(c1)。那么,

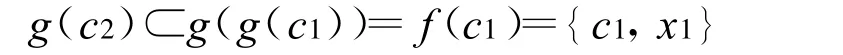
進一步,得到

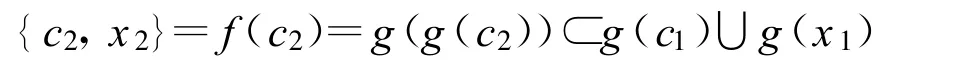
由于#g(c1)＞1,這同樣和g的嚴格單調性矛盾。因此 f不存在兩次迭代根。

3 例子

由引理1可知,f1的所有兩次迭代根都屬于F1(I)∪F2(I)∪F(I),即 f1的兩次迭代根只能在c1或者c2取到多值(見圖1)。根據定理1,則 f2不存在兩次迭代根(見圖2)。

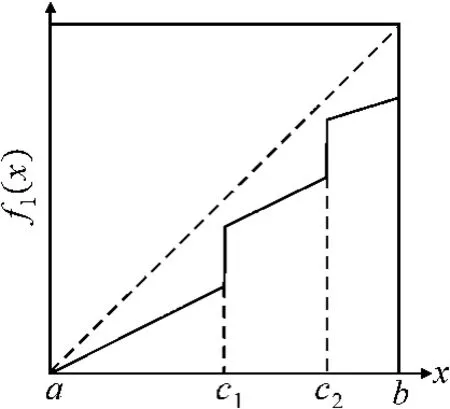
圖1 f1∈F(I)

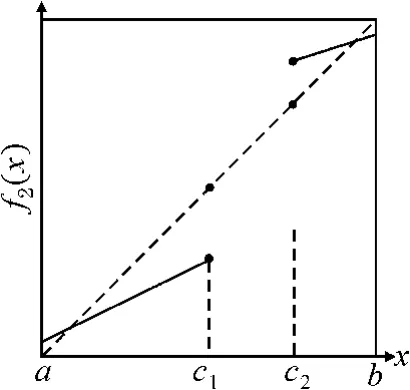
圖2 f2(ci)={ci,xi}

[1]Ch Babbage.Essay towards the calculus of functions[J].Philosoph.Transact,1815：389-423.

[2]S Bogatyi.On the nonexistence of iterative roots[J].Topology Appl,1997,76：97-123.

[3]M Kuczma.Functional equation in a single variable[M].Warszawa：Polish Scientific Publishers,1968.

[4]M Kuczma,B Choczewski,RGer.Iterative functional equations[M].Cambridge：Cambridge University Press,1990.

[5]Gy Targonski.Topics in Iteration Theory[M].G?ttingen：Vandenhoeck and Ruprecht,1981.

[6]Lin Li,Dilian Yang,Weinian Zhang.A note on iterative roots of PM functions[J],J.Math.Anal.Appl,2008,341：1482-1486.

[7]張景中,楊路.論逐段單調連續函數的迭代根[J].數學學報,1983,26：398-412.

[8]Weinian Zhang.PM functions,their characteristic intervals and iterative roots[J].Ann.Polon.Math,1997,65：119-128.

[9]Witold Jarczyk,Weinian Zhang.Also multifunctions do not like iterative roots[J].Elemente Math,2007,62：1-8.

[10]Lin Li,Justyna Jarczyk,Witold Jarczyk,Weinian Zhang.Iterative roots of mappings with a unique set-value point[J].Publ.Math.Debrecen,2009,75：203-220.