課堂教學中問題設計的有效性策略

諸建剛

學生學習數學的過程就是解決一系列問題的過程，教師通過提出的問題控制學生學習的內容和方向，保證學生學習的系統性、有效性，從而起到學習組織者、指導者的作用。教師如何在課堂教學中精心設計一系列好的問題就顯得非常重要，也值得去研究。這里，筆者結合自身多年的教學實踐，就這一問題的一個方面即問題設計的有效性策略來談談自己的一些認識。

1 現實性及應用性策略

問題的創設要注重其現實性，使所學的知識與相應的生活和生產實際相結合，使學生認識到數學知識的應用價值，這樣可激發學生的好奇心和求知欲，培養學生學以致用的意識和能力。

2 典型性及針對性策略

典型性即指抓住理解和應用知識的關鍵設置問題。如處理問題的典型思路和方法，知識間的內在聯系及易錯、易混之處，使問題擊中要害，學生能舉一反三，觸類旁通。如初中幾何計算通常采用分步計算和列方程（組）的方法，常用工具是相似三角形的比例式、勾股定理、面積變換等，教學時舉出相關例題讓學生從中掌握方法。

針對性即指根據課程標準對各知識點的要求程度（如了解、理解、掌握、運用等）設置問題，使問題難易得當，有的放矢。

3 程序性及階梯性策略

所創設的問題應按所學知識的發展過程組成一個循序漸進、具有內在聯系的問題體系，涉及的知識要從學生已有知識出發，逐步接近最近發展區，同時要針對學生知識出現的斷層和新舊知識的銜接點、學生的思維特點及認知規律設計問題的角度和梯度，層層推進，以達到讓學生“跳一跳，夠得著”的境界。這里應避免兩種傾向，一是問題程序過細，關節過于顯露，不利于思維的開展；二是程序過粗，隱含條件太多，學生思路不明確，不易抓住要點進行有目的的分析，容易導致學習方向的偏離。下面是方差一課的教學過程片段。

【情境設計：顯示打靶場面】

問題1：為了從甲、乙、丙3名射手中選拔一人參加射擊比賽，請你設計一種簡單易行的選拔方案。

學生回答：可分別計算甲、乙、丙3名射手射擊成績的平均數，誰的平均水平高，就選誰。

【新課】

教師提供甲、乙、丙3名射手的射擊成績：甲，10、7、7、7、7、7、4、7、7、7；乙，9、6、5、9、8、5、5、9、5、9；丙，8、6、6、7、6、4、7、5、5、6。

學生：1）分小組計算甲、乙、丙的射擊成績；2）發現除丙外，其他二人成績均為＝7；3）思維第一次受阻。

教師：激活思維。

問題2：平均數相等，射擊水平就完全一樣嗎？觀察數據特點，可從數據的穩定性上考慮。

學生小組討論，得出甲、乙數據特點：甲波動幅度大，但波動的數據少；乙波動幅度小，但波動的數據多。不能斷定哪個穩定性好，思維第二次受阻。教師：單看個別數據的波動幅度不能衡量一組數據的整體波動大小。

問題3：怎樣才能衡量整個一組數據的波動大小呢？

提供一種方案，供學生參考：將甲、乙兩數據以點的形式標注在平面直角坐標系里（坐標系略），然后用折線連接，確定7為中心線，從而觀察波動情況。1）能比較明顯地看到有多少數據在振動；2）數據偏離中心線的幅度有多少？結論：1）必須確定波動標準（一般取數據的平均數）；2）每個數據對整個波動情況都起作用；3）這種繪制圖像的方法仍然是定性的綜合印象。

問題4：怎樣定量地計算整個波動大小呢？

問題5：如何累計偏差？

學生：計算偏差的代數和，都為0。（無法比較，否定此法）

問題6：如何使正負偏差不互相抵消？

學生討論后得出兩種方法：1）給每個偏差加上絕對值后再相加；2）給每個偏差平方后再相加。

教師：通常采用方法2；小結計算偏差和的步驟。學生討論后得出步驟：1）計算數據平均數x；2）計算偏差，即每個數據與標準數據（）的差；3）計算偏差的平方和。

分別計算兩組數據的偏差的平方和：92.5、90、87.5；89、92、88、91、88。

教師：第一組的結果為12.5；第二組的結果為18，從計算可得出第一組比第二組穩定，但觀察數據顯然是第二組穩定。

問題7：觀察和計算為什么矛盾？學生：因為兩組數據個數不一樣。

問題8：在數據個數不一樣的情況下如何合理計算偏差？

學生：計算偏差平方的平均數。

教師：請同學們分別計算上述兩組數據偏差平方的平均數。

學生：算出第一組為4.17，第二組為3。

教師：現在觀察和計算還矛盾嗎？學生：……

教師：1）我們把一組數據偏差平方的平均數叫做這組數據的“方差”（板書課題“方差”）；2）請同學們總結計算方差的步驟。學生小組討論后給出步驟：1）計算數據的平均數；2）計算偏差，即每個數據與標準數據（）的差；3）計算偏差的平方和；4）除以數據個數。

問題9：對一般性的數據x1、 x2、 …xn，設其平均數為，你能寫出方差計算公式嗎？

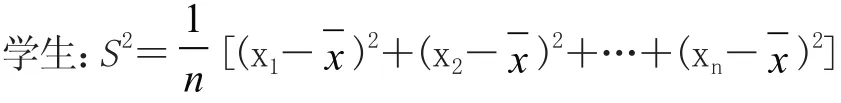
問題10：通過以上學習，你能講講方差的作用嗎？學生：用來估計一組數據波動的大小，方差越大，波動越大，數據越不穩定；反之，方差越小，波動越小，數據越穩定。

教師：1）標準差是用來恒量數據波動大小的另一個數學量；2）方差的單位是原數據單位的平方，而標準差的單位與原數據單位一致。

通過以上層層遞進、環環相扣的主問題，引發學生積極的思考和探索，不僅使學生掌握了抽象的方差公式，還讓他們知道了公式應用的環境和方法。

4 探究性及開放性策略

所編擬的問題要盡量創設懸念，體現思維沖突，使學生在知識上產生困惑，造成一種適度的心理焦慮。這樣可使學生產生質疑問題、探索求解的動機，促使他們積極主動地去探索知識，尋找規律，以達到激發思維，提高分析解決問題的能力的目的。同時，在創設問題時，要以基本知識為中心，通過各種變式手段營造開放性問題情境，引導學生從不同的角度去發散思維，開拓思路，增強自身的創新意識。

5 反思性及引申性策略

學生在解決問題時，一般情況下只會就題論題，其思想往往不夠嚴謹，帶有一定的直覺性，不大可能及時對自己的思維過程和解題方法進行整理、提升。因此，教師在解決原有問題的基礎上再設計一些迫使學生去反思的問題就很有必要。學生在教師的追問下進行反思，可深化對知識的理解，溝通新舊知識的聯系，優化解題方法，完善思維活動過程。此外，對所設計的一類問題及時進行歸納拓展，可促進學生對知識的同化和遷移，增強聯想類比能力，進一步提高思維活動效率。

總之，一個好的問題，能揭示事物的矛盾，喚起學生積極的思維，促使他們進入解決問題的角色，從而達到掌握知識、訓練能力、培養創新的目的。而要設計出一系列好的問題，需要教師課前精心設計，也需要掌握一些設計問題的策略和方法。