聯(lián)合生存概率準(zhǔn)則下的最優(yōu)再保險(xiǎn)研究

李 凱

（中央財(cái)經(jīng)大學(xué) 中國(guó)精算研究院，北京 100081）

0 引言

再保險(xiǎn)精算研究中，最優(yōu)再保險(xiǎn)一直備受關(guān)注，最早由Pesonen[1]提出使原保險(xiǎn)人風(fēng)險(xiǎn)的波動(dòng)（即方差）達(dá)到最小作為最優(yōu)準(zhǔn)則，求得最優(yōu)再保險(xiǎn)的形式。Gajek[2],Kaluszka[3]則以原保險(xiǎn)人方差最小作為最優(yōu)準(zhǔn)則，得到了最優(yōu)再保險(xiǎn)的統(tǒng)一形式。Young[4,5]研究了在Wang’s計(jì)算準(zhǔn)則下，效用函數(shù)期望達(dá)到最大時(shí)的最優(yōu)問題。以往大量的文獻(xiàn)僅僅考慮了原保險(xiǎn)人的利益，而在再保險(xiǎn)過程中，往往需要考慮再保險(xiǎn)雙方的利益，因此，將原保險(xiǎn)人和再保險(xiǎn)人相結(jié)合進(jìn)行研究亦頗具意義。曹云松[6]以原保險(xiǎn)人和再保險(xiǎn)人風(fēng)險(xiǎn)波動(dòng)的凸組合作為目標(biāo)函數(shù)，研究最優(yōu)再保險(xiǎn)的具體形式。在這些研究工作中，風(fēng)險(xiǎn)和效用函數(shù)常常作為衡量再保險(xiǎn)合同優(yōu)劣的標(biāo)準(zhǔn)。

原保險(xiǎn)人與再保險(xiǎn)人均希望獲得更多的保費(fèi)，并承擔(dān)較低的風(fēng)險(xiǎn)，最優(yōu)再保險(xiǎn)策略應(yīng)兼顧這兩方面的關(guān)系，更直觀的方法是以聯(lián)合生存函數(shù)作為優(yōu)化準(zhǔn)則，尋求聯(lián)合生存概率最大的再保險(xiǎn)安排。本文主要研究在給定的時(shí)間段內(nèi)，原保險(xiǎn)人和再保險(xiǎn)人的聯(lián)合生存概率問題，即雙方的理賠額均不超過各自收取的保費(fèi)和初始余額之和的概率。假設(shè)發(fā)生總額為S的理賠時(shí)，原保險(xiǎn)人承擔(dān)SI,再保險(xiǎn)人承擔(dān)剩余部分SR=S-SI。我們將分別討論成數(shù)再保險(xiǎn)（SR=（1-a）S）和停止損失再保險(xiǎn)(SR=(S-M)+)。本文選擇期望值保費(fèi)計(jì)算原理，即總保費(fèi)P=(1+θ1)E(S)，再保險(xiǎn)公司獲得保費(fèi) PR=(1+θR)E(SR), 而原保險(xiǎn)人保留剩余部分P1=P-PR，其中θ1θR為附加因子，通常θ1≤θR。原保險(xiǎn)人和再保險(xiǎn)人的初始余額則分別為U1、UR,則雙方聯(lián)合生存概率為{Pr(SI≤PI+UI,SR≤PR+UR)},我們將重點(diǎn)研究在給定條件下，使得聯(lián)合生存概率最大的再保險(xiǎn)策略，即

本文將通過推導(dǎo)和數(shù)值求解，分別給出成數(shù)再保險(xiǎn)（比例）和停止損失再保險(xiǎn)（非比例）的最優(yōu)自留額。相對(duì)而言，成數(shù)再保險(xiǎn)的最優(yōu)解比較簡(jiǎn)單且直觀，而停止損失再保險(xiǎn)的結(jié)果則需要更多的推導(dǎo)。并通過具體的例子，計(jì)算停止損失再保險(xiǎn)的最優(yōu)自留額以及最大生存概率。

1 最優(yōu)成數(shù)再保險(xiǎn)

成數(shù)再保險(xiǎn)是一種最簡(jiǎn)單的分保方式，是指原保險(xiǎn)人與再保險(xiǎn)人在合同中約定保險(xiǎn)金額的分割比例，將每一風(fēng)險(xiǎn)單位的保險(xiǎn)金額，按照約定的比例在分出公司與分入公司之間進(jìn)行分割的再保險(xiǎn)方式。成數(shù)再保險(xiǎn)的最大特征是“按比率”的再保險(xiǎn)，即原保險(xiǎn)人和再保險(xiǎn)人保險(xiǎn)金額的分?jǐn)偂⒈ｋU(xiǎn)費(fèi)的分?jǐn)偂①r款的分?jǐn)偠际前凑蘸贤?guī)定的同一比例來進(jìn)行的。

若理賠總額為S,那么原保險(xiǎn)人承擔(dān)S1=aS,再保險(xiǎn)人承擔(dān)SR=(1-a)S,其中0≤a≤1。雙方獲得的保費(fèi)收入分別為：

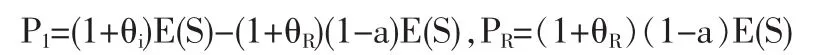
由于成數(shù)再保險(xiǎn)的保費(fèi)分?jǐn)傄彩前凑找欢ū壤M(jìn)行的，因此θ1=θR,而為了從理論上探討最優(yōu)再保險(xiǎn)問題，并與全文內(nèi)容保持一致，我們?nèi)詫ⅵ?、θR看成兩個(gè)不同的參數(shù)，定理1給出了成數(shù)再保險(xiǎn)的最優(yōu)分保比例。

定理1 在成數(shù)再保險(xiǎn)中，若原保險(xiǎn)人和再保險(xiǎn)人的初始余額則分別為U1、UR,保費(fèi)計(jì)算均遵循期望值原理，則原保險(xiǎn)人在準(zhǔn)則(1)下的最優(yōu)自留比例為

證明：在成數(shù)再保險(xiǎn)中，賠款的分?jǐn)偸前凑蘸贤?guī)定的比例來進(jìn)行的，故

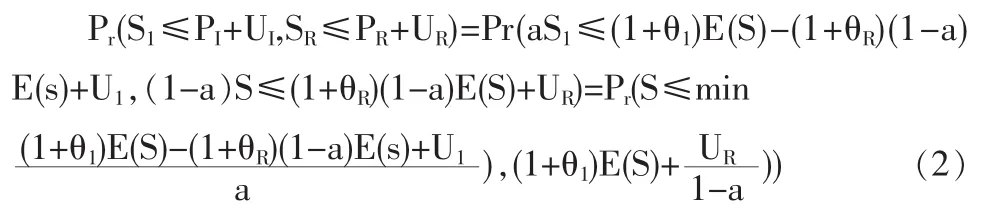
由于保險(xiǎn)公司初始余額、附加因子以及理賠額的期望均已給定，因此聯(lián)合生存概率(2)是一個(gè)關(guān)于a的函數(shù)，不妨設(shè)為G(a)，下面我們分情況討論：

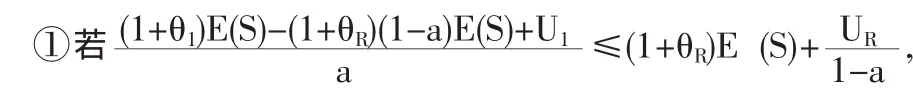
綜上所述，對(duì)于成數(shù)再保險(xiǎn)而言，由于 θI=θR，故(2)式在a=UI/UI+UR處取得最大值，從而得到了原保險(xiǎn)人的最優(yōu)自留比例。

特別的，若UR=0,則a*=1,即完全不分保時(shí)，聯(lián)合生存概率最大。這個(gè)結(jié)果是顯而易見的，此時(shí)聯(lián)合生存函數(shù)

故不分保時(shí)達(dá)到最優(yōu)。當(dāng)然這是一種很特殊的情形，如果再保險(xiǎn)人沒有初始余額，那么在分保后雙方的聯(lián)合生存概率總小于不分保時(shí)原保險(xiǎn)人的生存概率。

成數(shù)再保險(xiǎn)是一種最基本的再保險(xiǎn)形式，手續(xù)簡(jiǎn)單，且成本較低，雙方均按約定的比例分擔(dān)風(fēng)險(xiǎn)。若該比率與保險(xiǎn)公司初始余額的比率保持一致，則聯(lián)合生存概率可達(dá)到最大值。如原保險(xiǎn)人的初始余額較高，則應(yīng)自留更高比例的風(fēng)險(xiǎn)；如再保險(xiǎn)人的初始余額較高，則可分出更多的風(fēng)險(xiǎn)。

2 最優(yōu)停止損失再保險(xiǎn)

停止損失再保險(xiǎn)是以損失為基礎(chǔ)來確定再保險(xiǎn)當(dāng)事人雙方的責(zé)任，自留額以內(nèi)的損失完全由原保險(xiǎn)人承擔(dān)，而再保險(xiǎn)人對(duì)超過部分責(zé)任負(fù)責(zé)，即SR=(S-M)+。若損失金額（索賠額）x的密度函數(shù)為f(x)，其他條件不變，則再保險(xiǎn)人獲得保費(fèi)

若給定理賠額的分布，則原保險(xiǎn)人和再保險(xiǎn)人的聯(lián)合生存概率為M的函數(shù)G(M)，定理2給出了停止損失再保險(xiǎn)的最優(yōu)自留額及其存在的必要條件，符號(hào)和假定與前文均保持一致。

定理2 在停止損失再保險(xiǎn)中，原保險(xiǎn)人在準(zhǔn)則(1)下的最優(yōu)自留額M*需同時(shí)滿足如下條件：

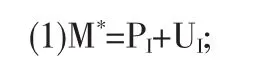
(2)損失金額S的分布函數(shù)在M*處的值F(M*

(3)聯(lián)合分布函數(shù)在M*處的值不小于不分保時(shí)原保險(xiǎn)人的生存概率，即G(M*)≥Pr(S≤P+UI).

證明：原保險(xiǎn)人和再保險(xiǎn)人的聯(lián)合生存概率為M的函數(shù)，由停止損失再保險(xiǎn)的性質(zhì)，有：

G(M)=Pr(S1≤PI+UI,SR≤PR+UR)=Pr(S1≤PI+UI,SR≤PR+UR,SM)+Pr(SI≤PI+UI,SR≤PR+UR,S＞M)=Pr(SPI+UI,S≤M)+Pr(M≤PI+UI,S-M≤PR+UR,S＞M)

其中，UI、UR為正常數(shù)，PI、PR是關(guān)于 M 的函數(shù)， 對(duì) PR求導(dǎo)可得：

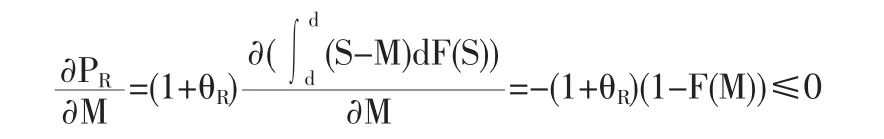
下面，我們分兩種情況討論：

①若M≥M*，則M≤PI+UI,

G(M)=Pr(S≤M)+Pr(M＜S≤PR+UR+M)=Pr(S≤PR+UR+M)

我們對(duì)函數(shù)G(M)求導(dǎo)：

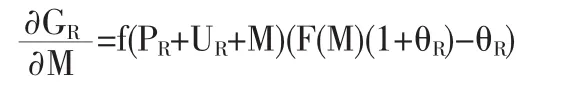
其中f、F分別是損失分布的密度函數(shù)和分布函數(shù)，F(xiàn)(M)==0，并設(shè)該點(diǎn)為。函數(shù)G(M)在左側(cè)遞減，在右側(cè)遞增。若M*≤，則G(M)在M=0處取得最大值，而這意味著全部風(fēng)險(xiǎn)分出，這是不合理的，最優(yōu)自留額不存在。因此，最優(yōu)解存在的一個(gè)必要條件是M*＞，即損失金額S的分布函數(shù)在M*處的值

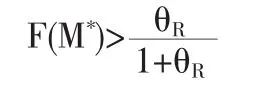
則函數(shù)G(M)在M*處取得最大值。

②若 M＞M*，則 M＞PI+UI,G(M)=Pr(S≤PI+UI),在此情形下，

綜上所述，停止損失再保險(xiǎn)的最優(yōu)自留額須滿足定理?xiàng)l件(1)、(2)，并且最優(yōu)聯(lián)合生存概率不應(yīng)小于不分保時(shí)原保險(xiǎn)人的生存概率。

需要特別注意的是，函數(shù)G(M)在M*處是不連續(xù)的。左極限

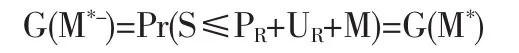
而右極限

顯然G(M*-)＞G(M*+)。事實(shí)上，在情形①中，風(fēng)險(xiǎn)自留額不超過原保險(xiǎn)人保費(fèi)與初始余額之和，我們只需考慮再保險(xiǎn)人的生存概率；情形②中，風(fēng)險(xiǎn)自留額大于原保險(xiǎn)人保費(fèi)與初始余額之和，所以必須保證原保險(xiǎn)人損失額小于保費(fèi)與初始余額之和，而此時(shí)再保險(xiǎn)人不需要理賠，必然生存。由于我們考慮的是雙方同時(shí)生存的概率，停止損失再保險(xiǎn)合同又可以看成是一類分段函數(shù)，從而導(dǎo)致聯(lián)合生存概率函數(shù)在M*處不連續(xù)的。下面，我們通過兩個(gè)實(shí)際的例子，計(jì)算停止損失再保險(xiǎn)的最優(yōu)自留額。

3 實(shí)例分析

指數(shù)分布：若理賠額S服從期望為100的指數(shù)分布，即f(S=x)，μ=100。若停止損失再保險(xiǎn)的自留額為M，則再保險(xiǎn)人獲得保費(fèi)

其中，附加因子θ1=0.1,θR=0.2，雙方的初始余額分別為UI=40，UR=10。 運(yùn)用數(shù)值方法，可獲得方程 （1+θI）μ-(1+θR）μe=M 的根 M*≈110.1,此時(shí)顯然 。 聯(lián)合生存概率G(M*)=0.7980。如不分保，原保險(xiǎn)人的生存概率為

F(S≤P+UI)=0.7769＜G(M*)

因此，M*≈110.1即為停止損失再保險(xiǎn)在聯(lián)合生存概率準(zhǔn)則下的最優(yōu)自留額。

帕累托分布：若理賠額S服從期望為100的帕累托分布，即 f(S=x)，其中 k=400,α=5,其他條件同上，則再保險(xiǎn)人獲得保費(fèi)

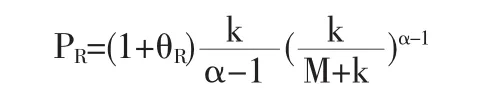
原保險(xiǎn)人保留保費(fèi)

F(S≤P+UI)=0.7956＜G(M*)

因此，M*≈110.4為帕累托分布下停止損失再保險(xiǎn)的最優(yōu)自留額。

4 小結(jié)

本文以原保險(xiǎn)人和再保險(xiǎn)人的聯(lián)合生存概率最大化為準(zhǔn)則，分別探討了兩類常見的再保險(xiǎn)形式：成數(shù)再保險(xiǎn)和停止損失再保險(xiǎn)的最優(yōu)策略。研究結(jié)果表明，成數(shù)再保險(xiǎn)的最優(yōu)策略與雙方的初始余額直接相關(guān)。而停止損失再保險(xiǎn)的最優(yōu)策略須使得自留額與原保險(xiǎn)人剩余保費(fèi)相等，同時(shí)滿足最優(yōu)解存在的必要條件。此外還通過具體實(shí)例驗(yàn)證結(jié)論。基于該準(zhǔn)則的最優(yōu)再保險(xiǎn)策略兼顧了再保險(xiǎn)當(dāng)事人雙方的利益，可為保險(xiǎn)公司與再保險(xiǎn)公司的決策提供有力依據(jù)。

[1]Pesonen,M.L.Optimal Reinsurances[J].Scandinavian Actuarial Journal,1984,84.

[2]Gajek,L.,Zagrodny,D.Insurer’s Optimal Reinsurance Strategies[J].Insurance:Mathematics and Economics,2000,27.

[3]Kaluszka,M.Optimal Reinsurance Under Mean 2 Variance Premium Principles[J].Insurance:Mathematics and Economics,2001,28.

[4]Young,V.R.Optimal Insurance under Wang’s Premium Principle[J].Insurance:Mathematics and Economics,1999,25.

[5]Young,V.R.Discussion of Christofides’Conjecture Regarding Wang’s Premium Principle[J].ASTIN Bulletin,1999,29(2).

[6]曹云松.最優(yōu)再保險(xiǎn)的研究[D].浙江大學(xué)碩士論文，2006.