新上市變質(zhì)品的EPQ模型研究

陳六新 ，李 軍，謝天帥

(1.西南交通大學(xué) 經(jīng)濟管理學(xué)院，成都 610031；2.重慶郵電大學(xué) 經(jīng)濟管理學(xué)院，重慶 400065)

0 引言

變質(zhì)產(chǎn)品廣泛存在于日常生產(chǎn)和生活中，如生鮮食品、水果、蔬菜、海鮮、電子類產(chǎn)品等，在存儲流通過程中隨時間的增加，其數(shù)量會因腐爛、損壞等原因而減少。目前我國變質(zhì)商品在流通過程中造成的各種損耗非常大(水果、蔬菜采后的損失高達35%，肉類及水產(chǎn)品亦達10～15%)，每年僅變質(zhì)食品采后的各種損耗之和高達千億元之巨[1]。因而，對變質(zhì)品生產(chǎn)庫存控制規(guī)律的研究具有極強的現(xiàn)實意義。

經(jīng)典的經(jīng)濟訂貨模型(EOQ)適用于產(chǎn)品成熟期(即需求為常數(shù))，沒有考慮產(chǎn)品具有變質(zhì)的現(xiàn)象。1963年Ghare和Schrader研究了變質(zhì)率為常數(shù)處于成熟期的變質(zhì)品瞬時補貨策略[2]。由于任何新上市產(chǎn)品都要經(jīng)歷市場擴張或成長期，在這一時期單位時間的需求隨時間而增加，經(jīng)過一段時間增長之后，進入成熟期，產(chǎn)品的需求相對穩(wěn)定[3]。關(guān)于新上市變質(zhì)品的瞬時補貨策略研究較多。1995年Hill建立了需求在成長期呈指數(shù)增加，在成熟期穩(wěn)定為常數(shù)的訂貨模型[4]。Hill的研究沒有考慮零售商可以缺貨的情形，1998年Mondal和Pal將Hill的研究擴展為允許缺貨且缺貨完全拖后供給，給出了先補給后缺貨情形的訂貨策略[5]。1999年Wu等建立了缺貨部分拖后供給的變質(zhì)品訂貨模型，認為在缺貨期間愿意等待的顧客會隨等待時間的增加而減少，拖后供給因子是實際等待時間的減函數(shù)，研究了缺貨部分拖后供給情形下的訂貨策略[6]。2000年Wu和Ouyang研究了在先缺貨后補給和先補給后缺貨兩種情形下且缺貨完全拖后供給的零售商訂貨策略[7]。2001年Wu[8]和 2003年Giri[9]建立變質(zhì)率時變且服從weibull分布、缺貨部分拖后供給的EOQ模型，研究了零售商的補貨策略。2007年Deng等研究了在先補給后缺貨、成長期可以缺貨且缺貨完全拖后供給情形下的訂貨策略，并指出文獻[5]和文獻[7]在模型求解中存在的問題[10]。Skouri等將文獻[10]的模型擴展到了先缺貨后補給且缺貨部分拖后供給的情形[11]。文獻[2～10]的新上市變質(zhì)品庫存研究主要考慮了變質(zhì)率是否時變、是否允許缺貨、先補給還是先缺貨、缺貨是否完全拖后供給等因素，研究了零售商的訂貨策略，沒有考慮邊補貨邊需求的EOQ模型(即經(jīng)濟生產(chǎn)批量模型，EPQ)。

對于邊補貨邊需求新上市變質(zhì)品EOQ模型的研究很少。2008年張旭梅等研究了新上市變質(zhì)品在成長期的生產(chǎn)庫存[12]。2006年Manna和Chaudhuri建立了在不允許缺貨或允許缺貨且缺貨完全拖后供給情形下單位生產(chǎn)成本隨生產(chǎn)規(guī)模的擴大而降低的經(jīng)濟生產(chǎn)批量模型[13]。但是，其在模型中假定“成長期不停止生產(chǎn)”，對于某些成長期較長的新上市變質(zhì)品(如電子類產(chǎn)品)而言，若成長期不停止生產(chǎn)，會使庫存成本和損耗成本過大、生產(chǎn)庫存策略非最優(yōu)，導(dǎo)致不經(jīng)濟現(xiàn)象。故需要取消文獻[13]的該項假定，即在“成長期也可以停止生產(chǎn)”的條件下來研究新上市變質(zhì)品的生產(chǎn)庫存策略。

1 假定與符號

由于電子元件對存放環(huán)境的溫度和濕度要求苛刻，在存放過程中易出現(xiàn)品質(zhì)下降的問題，例如由于溫度和濕度的影響而使得產(chǎn)品失去功能，該類產(chǎn)品具有變質(zhì)的特征。電子類產(chǎn)品由于市場競爭激烈和產(chǎn)品生命周期縮短，在成長期內(nèi)產(chǎn)品的需求快速增長，需求不可能無限制地增長，在成熟期需求相對穩(wěn)定。因此對新上市變質(zhì)品要考慮成長期和成熟期需求不同而制定庫存策略[13]。本文的研究基于以下假設(shè)：

（1）需求呈階梯型。具有廣泛接受度的新產(chǎn)品在生命周期的成長期其需求隨時間變化呈遞增趨勢，在成熟期需求相對穩(wěn)定。本文考慮新產(chǎn)品的第一生產(chǎn)周期長于成長期。

（2）生產(chǎn)率為需求率的倍數(shù)。

（3）生產(chǎn)有規(guī)模效應(yīng)，生產(chǎn)成本隨生產(chǎn)規(guī)模的增大而減少。

（4）物品存在變質(zhì)現(xiàn)象，產(chǎn)品進入庫存系統(tǒng)就開始變質(zhì)損耗，變質(zhì)率為常數(shù)。

（5）生產(chǎn)庫存系統(tǒng)不允許缺貨。

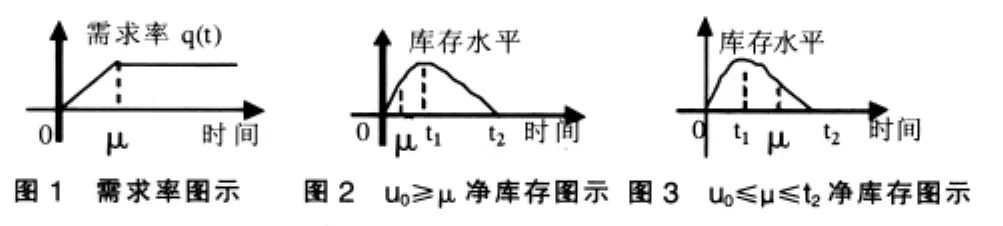
文中符號規(guī)定如下：p為產(chǎn)品的銷售價格；C表示固定啟動成本；C2表示單位產(chǎn)品單位時間的庫存費用；t1是生產(chǎn)期；t2是生產(chǎn)周期；產(chǎn)品的需求率為，其中需求增長率D和成長期μ均為正常數(shù) (如圖1)；R=βq表示生產(chǎn)率(常數(shù) β 大于 1)；C1=α1q-γ表示單位生產(chǎn)成本，其中 α1、γ 為正常數(shù)且γ≠2，可以看出，單位生產(chǎn)成本是生產(chǎn)率的減函數(shù)[13]；θ表示產(chǎn)品的變質(zhì)率(0＜θ＜1為常數(shù))。

2 模型建立及求解

根據(jù)上述假定知，庫存函數(shù)應(yīng)滿足的微分方程為：

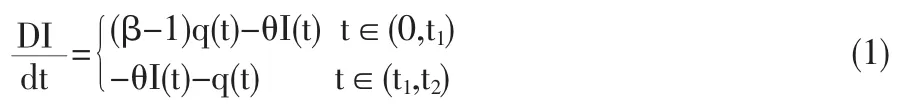
本文的主要目的是尋求新上市產(chǎn)品第一個生產(chǎn)周期的最優(yōu)生產(chǎn)策略①若第一周期的長度小于 T1＜μ，則第二周期的計算只需將式(1)的 t∈(0＜t1)和 t∈(t1，t2)分別更改為 t∈(T1，T1+t1)和 t∈(T1+t1，T1+t2)，重復(fù)本文后面的運算過程即可得到最優(yōu)生產(chǎn)策略；當(dāng)T1≥μ時，則有q(t)為常數(shù)，已有經(jīng)典文獻研究。其余周期以此類推。，由于其需求率為一個階梯型分段函數(shù)，所以需分三種情況進行討論：(1)成長期不停止生產(chǎn)(庫存示意如圖2)；(2)成長期大于生產(chǎn)期小于生產(chǎn)周期(庫存示意如圖3)；(3)成長期大于生產(chǎn)周期。

2.1 成長期不停止生產(chǎn)模型(t1≥μ)

在成長期不停止生產(chǎn)的情況下，根據(jù)式(1)，可以求得庫存函數(shù)為：

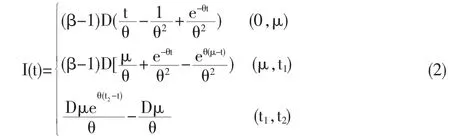
由于在t1時刻庫存函數(shù)是連續(xù)變化的，即，由(2)式可得

由式(2)和式(3)可得，賣出產(chǎn)品的數(shù)量為：

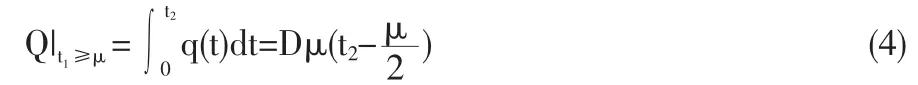
庫存費用為：

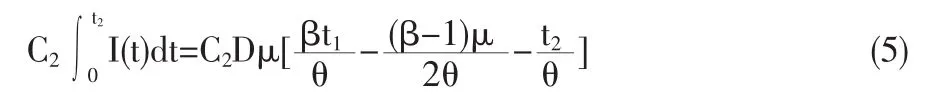
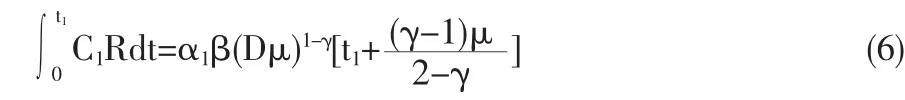
生產(chǎn)批量為

由式(3)～(6)，得到總利潤函數(shù)為：

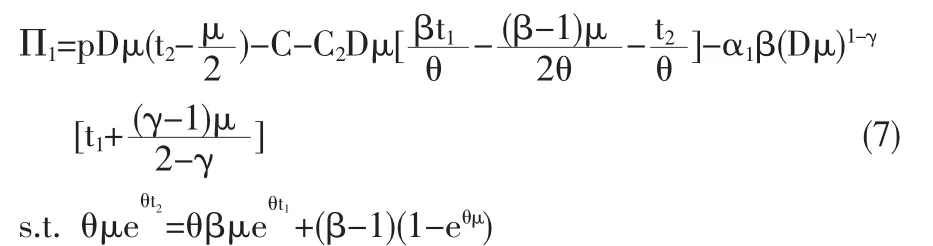
2.2 成長期大于生產(chǎn)期小于生產(chǎn)周期(t1≤μ＜t2)

在成長期大于生產(chǎn)期小于生產(chǎn)周期的情況下，根據(jù)式(1)，庫存函數(shù)應(yīng)為：

由于在t1時刻庫存函數(shù)是連續(xù)變化的，故有

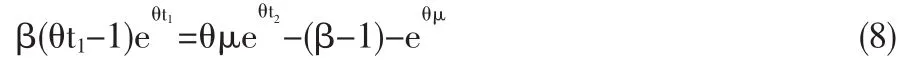
生產(chǎn)批量為：

類似于2.1節(jié)的計算，可得總利潤函數(shù)為：

2.3 成長期大于生產(chǎn)周期模型(t2≤μ)

在成長期大于生產(chǎn)周期的情況下，根據(jù)式(1)，庫存函數(shù)應(yīng)為：

由于在t1時刻庫存函數(shù)是連續(xù)變化的，故有

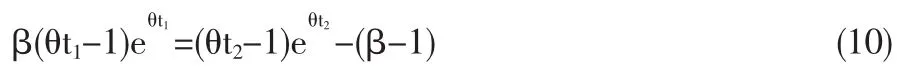
類似于2.1節(jié)的計算，可得總利潤函數(shù)為：

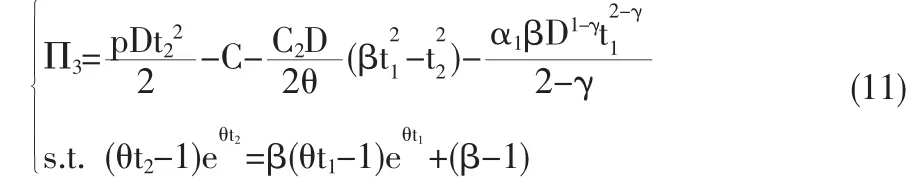
以 π(t1，t2)表示在(0，t2)的單位時間平均利潤，由式(7)、式(9)和式(11)可得，平均利潤函數(shù)為：

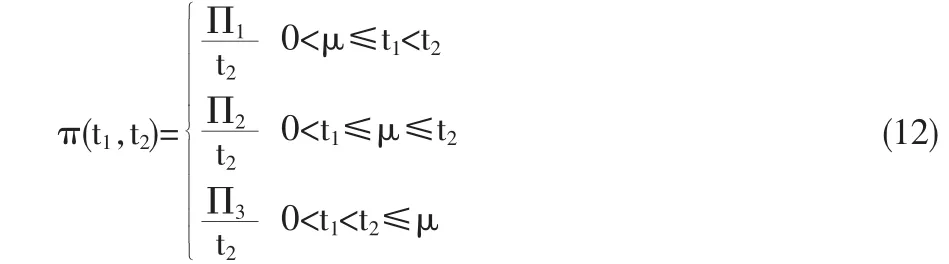
2.4 最優(yōu)生產(chǎn)策略的確定

為了得到使 π(t1，t2)最大的 t1和 t2，由式（3）、（8）式和式（10），可得 t1是 t2的函數(shù)，π(t1，t2)實際是 t2的一元分段函數(shù)π*(t2)，不能從整體上說明它的凹凸性。為了得到最優(yōu)的生產(chǎn)策略，給出如下引理。

引理 若f(x)是定義在[0，+∞)中的關(guān)于x的嚴格凹函數(shù)，x0＞0 為其駐點，則的最大值點必不大于x0。

證明 f(x)是定義在[0，+∞)中的關(guān)于x的嚴格凹函數(shù)，對于 x1＞x0＞0，有 f(x0)＞f(x1)，即故引理成立。

下面根據(jù)式(12)，分析π*(t2)特性，得到最優(yōu)解的存在區(qū)間，并得到求最優(yōu)解的步驟：

(1)當(dāng) t1≥μ 時，由式(3)可得 t1是 t2的函數(shù)，則 Π1(t1，t2)和π(t1，t2)均是 t2的一元函數(shù)，分別用 Π1*(t2)和 π1(t2)表示。 設(shè)的解為 t2=μ1，當(dāng) t1=μ 時使式(3)成立的 t2為 μ2。 若μ2＞μ1，則此種情形不存在最優(yōu)策略。 若 μ2≤μ1，則由Π1*為嚴格凹且由引理知，π1(t2)滿足條件的最大值點 t2*1必存在于[μ2，μ1]中。

(2)當(dāng) t1≤μ≤t2時，由式(8)可得 t1是 t2的函數(shù)，則 π(t1，t2)實際是 t2的一元函數(shù) π2(t2)。 當(dāng) t1=μ時，式(3)與式(8)相同，故使得式(8)成立的 t2仍為μ2。若 μ＞μ2，則此種情形不存在最優(yōu)策略。若 μ≤μ2，則由連續(xù)函數(shù) π2(t1)的滿足條件的最大值點 t2*2必存在于[μ，μ2]中。

(3)當(dāng) t2≤μ 時，由式(10)可得 t1是 t2的函數(shù)，π(t1，t2)是 t2的一元函數(shù)在(0,μ]上連續(xù)，所以 π3(t2)在(0,μ]存在最大值點t2*3。

綜上所述，可以得到問題最優(yōu)解的確定步驟：

①根據(jù)已知參數(shù)，如上確定三個搜索區(qū)間，編寫Matlab程序，在相應(yīng)的區(qū)間搜索出對應(yīng)的最大值點t2*i。

②將 t2*i代入 πi(t2)(i=1，2，3)中，使 πi(t2)最大的 t2*i即為最優(yōu)解t2*，并求出最優(yōu)的t1，從而得到最優(yōu)生產(chǎn)批量Q*。

3 算例及參數(shù)分析

某制造企業(yè)主要生產(chǎn)某種變質(zhì)品，相關(guān)的參數(shù)如下：C=100,θ=0.1,p=15,D=200，C2=1.5,μ=5,α1=2000,β=4,γ=0.95。 按文獻[13]的模型，借助數(shù)學(xué)軟件Matlab7.1可得t1=5.0016，t2=9.9458，第一周期的生產(chǎn)批量為10006，最優(yōu)平均利潤為1945.70；根據(jù)本文模型可得t1=4.6066，t2=8.9940，第一周期的生產(chǎn)批量8488，最優(yōu)平均利潤為2003.25，很明顯本文得到的生產(chǎn)策略優(yōu)于前者。故文獻[13]的模型“成長期不停止生產(chǎn)”的限制條件不合理，得到的策略可能是低效的(見表1(a),表1(b))。

將上例的單位庫存成本、變質(zhì)率和需求增長率分別取不同的值，按照文獻[13]的模型計算得表1(a)、表2(a)和表3(a)，利用本文的模型計算得表1(b)、表2(b)和表3(b)，將所得數(shù)據(jù)進行比較可以得到如下結(jié)論：

本模型得到的策略是有效的，而且?guī)齑娉杀驹礁摺⒆冑|(zhì)率越低和需求增長率越大，本文策略的有效性越明顯；當(dāng)庫存成本增加時生產(chǎn)周期縮短，生產(chǎn)期可能從大于成長期變?yōu)樾∮谛枨笤鲩L期，平均利潤降低；反之亦然。變質(zhì)率增加時生產(chǎn)期增加，生產(chǎn)周期縮短，平均利潤減小；反之亦然。需求增長率增加時生產(chǎn)期縮短，生產(chǎn)周期縮短，平均利潤增加；反之亦然。

在實際生活中，單位庫存成本和變質(zhì)率增加必然會引起庫存費用和損耗費用的增加，利潤減少，適當(dāng)縮短經(jīng)營周期，減少庫存和損耗，可以增加收益，從變化的結(jié)果看與實際情況相符合。根據(jù)靈敏度分析，庫存和損耗變化的情況下，要獲取最大利潤，管理者應(yīng)該通過有效辦法減少庫存成本和損耗成本。

4 結(jié)束語

本文研究了新上市變質(zhì)品的生產(chǎn)策略，通過分析得到了尋求最優(yōu)生產(chǎn)策略的方法，擴展了文獻[13]的模型，豐富了庫存理論。利用數(shù)值仿真，對參數(shù)變化在本文和在文獻[13]下所得結(jié)果進行比較，說明“成長期不停止生產(chǎn)”的限制條件是不合理的，可能導(dǎo)致所得到的策略是低效的。這一結(jié)論為生產(chǎn)管理部門的決策提供了有力的理論依據(jù)。該問題可以考慮允許缺貨經(jīng)濟生產(chǎn)批量做進一步研究。

表1 (a)庫存成本對平均利潤及生產(chǎn)策略影響

表1 (b)庫存成本對平均利潤及生產(chǎn)策略影響

表2 (a)變質(zhì)率對平均利潤及生產(chǎn)策略影響

表2 (b)變質(zhì)率對平均利潤及生產(chǎn)策略影響

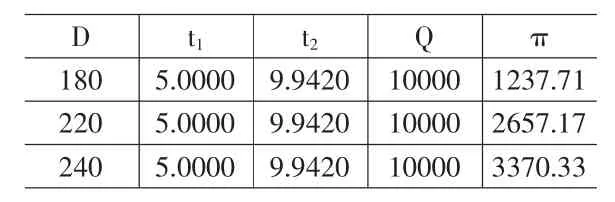
表3 (a)需求增長率對平均利潤及生產(chǎn)策略影響

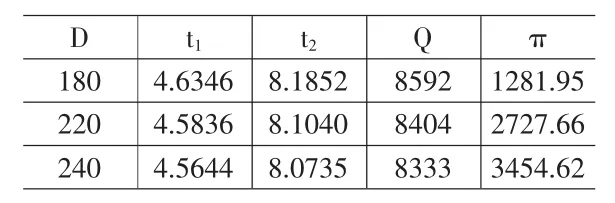
表3 (b)需求增長率對平均利潤及生產(chǎn)策略影響

[1]龔樹生,梁懷蘭.生鮮食品的冷鏈物流網(wǎng)絡(luò)研究[J].中國流通經(jīng)濟,2006,(2).

[2]Ghare P.,Schrader G.A Model for Exponentially Decaying Iinventories[J].Journal of Industrial Engineering,1963,（14）.

[3]PandaS,SenapatiS,Basu M.OptimalReplenishmentPolicy for Perishable Seasonal Products in a Season with Ramp-Type Time Dependent Demand[J].Computers&Industrial Engineering,2008,(54).

[4]Hill R.M.Inventory Model for Increasing Demand Followed by Level Demand[J].Journalofthe OperationalResearch Society,1995,(46).

[5]MondalB.,PalA.K.OrderLevelInventorySystem with Ramp Type Demand for Deteriorating Items[J].Journal of Interdisciplinary Mathematics,1998,(1).

[6]Wu J.W.,Lin C.,Tan B.,Lee W.C.An EOQ Inventory Model with Ramp Type Demand Rate for Items with Weibull Deterioration[J].Information and Management Science,1999,10(3).

[7]Wu K.S.,Ouyang L.Y.A Replenishment Policy for Deteriorating Items with Ramp Type Demand Rate[C].Proceedings of the National Science Council,Republic of China,Part A:Physical Science and Engineering,2000,24(4).

[8]Wu K.S.An EOQ Inventory Model for Items with Weibull Distribution Deterioration,Ramp Type Demand Rate and Partial Backlogging[J].Production Planning and Control,2001,12(8).

[9]Giri B.C.,Jalan A.K.,Chadhuri K.S.Economic Order Quantity Model with Weibull Deterioration Distribution,Shortage and Ramp-Type Demand[J].International Journal of Systems Science,2003,34(4).

[10]Deng Peter Shaohua,Lin Robert H.J.,Chu Peter.A Note on the Inventory Models for Deteriorating Items with Ramp Type Demand Rate[J].European Journal of Operational Research,2007,178.

[11]Skouri K.,Konstantaras I.,Papachristos S.,Ganas I.Inventory Models with Ramp Type Demand Rate,PartialBacklogging and WeibullDeterioration Rate[J].European Journal of Operational Research,2009,192.

[12]張旭梅,邱晗光,陳軍.補貨能力影響部分短缺量拖后率的邊補貨邊需求EOQ模型[J].中國管理科學(xué)，2008，16(1).

[13]Manna S.K.,Chaudhuri K.S.An EOQ Modelwith Ramp Type Demand Rate,Time Dependent Deterioration Rate,Unit Production Cost and Shortages[J].European Journal of Operational Research,2006,171.