2.4m跨聲速風洞大型飛機試驗不確定度評估

謝疆宇,吳軍強,鐘世東 ,王義慶 ,魏 志

(中國空氣動力研究與發展中心,四川綿陽 621000)

0 引 言

風洞試驗是開展空氣動力學研究的最主要手段。風洞試驗質量不僅影響飛行器實際飛行性能的正確預測,關系到飛行器的研制質量和研制水平,而且還直接決定著一座風洞的實際應用和作用發揮,在生產性風洞中居于至關重要的地位,是實驗空氣動力學領域的主要研究范疇之一。

傳統基于重復性試驗精度的質量評估方法在風洞試驗質量控制中應用較為廣泛,并有力地促進了實驗空氣動力學的發展。但傳統質量評估方法僅從試驗結果出發,做出綜合評估,未能分解試驗儀器、設備校準和試驗數據生產過程中各環節涉及的各種誤差源影響,因此還應需要不斷完善和發展新的質量評估方法,進一步提高試驗質量。上世紀90年代初,國際標準化組織頒布實施了《測量不確定度表示指南》,將不確定度評估方法推薦為計量領域的國際標準,并在世界各國得到執行和廣泛應用。隨后,AGARD發表了題為風洞試驗質量評估(AGARD-AR-304)的報告,將不確定度評估方法引入了風洞試驗[1]。該方法克服了精度方法的不足,從試驗過程中各種基本誤差源出發,通過全面考察試驗設備和過程,定量分析不同誤差源對最終試驗結果的影響,發展了科學評估分析風洞試驗數據質量的工程算法,目前已為各風洞試驗單位廣泛采用。

中國大型飛機研制工程正在進行,相關風洞試驗已經全面展開。由于大型飛機對遠航程、大運載量和安全性、經濟性等方面的追求,對風洞試驗質量提出了很高的要求。2.4m跨聲速風洞是中國目前唯一的2m量級大型試驗設備,在中國大型飛機研制項目中發揮著基礎性平臺的作用。因此,迫切需要對該風洞的試驗數據質量進行準確評估和有效控制,以滿足大型飛機跨聲速氣動力試驗的苛刻要求,減小研制風險。為此,以2.4m跨聲速風洞為研究平臺,從不確定度評估原理出發,建立了該風洞大型飛機試驗質量評估方法,并探索改進提高其試驗質量的有效措施。

1 不確定度評估原理

1.1 不確定度計算方法

1.1.1 AGARD計算方法概述

風洞試驗是一種間接測量過程,最終試驗結果受諸多基本誤差源的影響,這些基本誤差源直接影響到若干被測變量,然后通過數據處理方程傳播到最終結果中。假設某一試驗結果r由n個基本被測變量x1,x2,…xn求得,其函數關系式為：r=f(x1,x2…xn),對方程按 Taylor級數展開并略去二階以上小量,可以得出試驗結果的不確定度表達式[2]

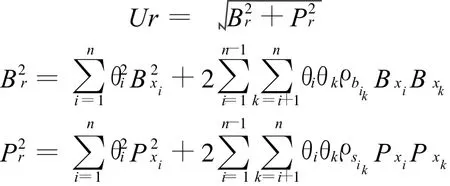
其中：θi=?r/?xi為靈敏度系數,Ur、Br、Pr分別為最終試驗結果的不確定度、偏離極限和精度極限,Bxi、Pxi分別為被測變量xi的偏離極限和精度極限,ρbik、ρsik分別為被測變量 xi、xk偏離極限與精度極限的相關系數。在絕大多數的風洞試驗中可以認為各獨立被測變量的精度極限彼此獨立、互不相關,即ρ=0。對于大部分的獨立被測變量,其偏離極限也可以近似認為是互不相關的,即ρbik=0。而對于以下兩類被測變量,一是使用同一個儀器測量的變量;二是使用相同校準裝置校準的不同儀器所測量的變量,其部分偏離極限是相關的,即ρbik≠0。

1.1.2 對AGARD方法的補充

由于AGARD計算方法僅考慮了可以通過數據處理公式傳播的不確定度,但試驗結果的分散性并不是全部由那些通過數據處理公式傳播的基本參數引起,比如試驗段模型區馬赫數控制精度、模型活動舵面安裝精度、模型姿態角定位不準確而影響天平測量結果以及模型的振動特性等都不能通過數據處理公式反映出來。計算結果表明,如果不考慮這些因素用AGARD方法計算得到的精度極限則比重復性試驗精度小很多。本文采用線性插值的方法,分別計算馬赫數、模型姿態、舵面安裝精度引起的不確定度,而通過連續采集結果分析模型振動特性,確定由此引起的氣動力測量不確定度,再將這些分量與通過公式計算結果結合起來,計入最終結果的不確定度中。

1.2 不確定度源分析及其量值標定

研究對象沒有包含由洞壁干擾、支撐干擾、Re數影響修正等帶來的不確定度,重點放在試驗數據采集處理過程及設備、試驗環境的不確定度上。

按照AGARD-AR-304介紹的方法,對各測試系統及設備統一進行了仔細的校準,標定了2.4m跨聲速風洞試驗基本參數的不確定度量值,表1給出主要結果。結果表明該風洞基本參數的不確定度水平與文獻[1]給出的美國阿諾德工程發展中心4T、16T風洞當時的水平基本相當。

表1 2.4m跨聲速風洞基本參數的不確定度Table1 The uncertainties for instrumentation and input parameters of 2.4m transonic wind tunnel

1.3 不確定度評估軟件開發

不確定度評估的原理和方法比較簡單并易于理解,但是其計算過程十分復雜,尤其是要涉及到多個自變量函數求偏導,文獻[2]介紹,試驗結果共19個,獨立參數23個,靈敏度系數θi=?r/?xi共計19×23=437個,組成一個龐大的矩陣{θi=?r/?xi}。因此,必須通過計算機編程實現自動計算,才能得到有意義的結果。文獻[3]介紹了一種基于C++語言的不確定度計算程序AUL(Automatic Uncertainty Library),文獻[4]介紹了一種在Turbo PASCAL V7.0集成環境下完成符號計算程序SMP(Symbolic Math Program)。為實時開展不確定度評估,充分利用2.4m跨聲速風洞現有的數據處理平臺,并結合MATLAB提供的符號計算工具箱,開發了基于MATLAB引擎的MATLAB和C++Builder聯合編程方法的評估軟件,實現了數據處理和不確定度計算的同步實施。

數據處理公式、基本參數的符號、參數不確定度的符號可存儲在數據庫中,以利于程序的標準化,適應不同的數據處理公式。這些基本參數和公式通過MATLAB引擎以符號的形式輸入MATLAB工作空間后,最終結果則成為由基本參數組成的符號表達式。用最終結果的符號表達式對每一個基本參數進行符號微分求得各項靈敏度系數。將各階梯基本參數及其不確定度的值代入不確定度計算公式,得到最終結果的不確定度值。軟件結構如圖1。

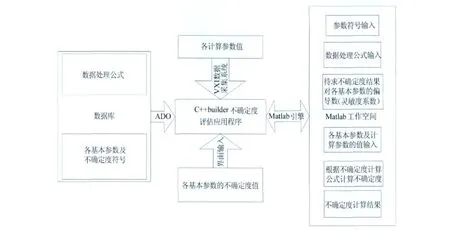
圖1 不確定度評估軟件結構及計算流程Fig.1 Structure of the uncertainty analysis program

2 評估結果分析與討論

采用編制的不確定度評估軟件,對某大型飛機試驗數據開展了不確定度評估分析,得到2.4m跨聲速風洞大型飛機試驗的質量水平,確定了其影響大飛機試驗質量的主要因素。

2.1 某大型飛機模型試驗結果不確定度評估分析

表2給出某大型飛機巡航狀態下縱向3個氣動力(矩)系數的重復性試驗精度,表3給出其不確定度評估計算結果(試驗過程中模型及其部件經過數次拆裝)。

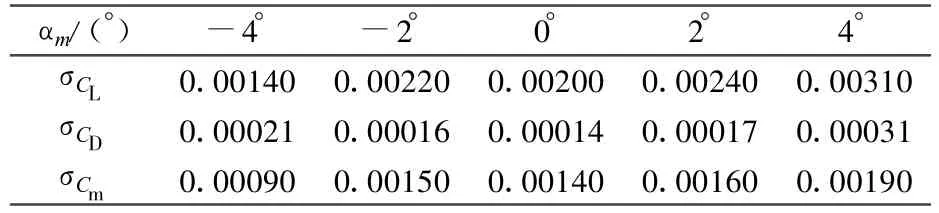
表2 某大型飛機重復性試驗精度T able 2 The standard error of test results of certain large aircraft

從表2和3中可以看出,重復性試驗精度與計算得到的精度極限相當,而不確定度約為精度極限的2～4倍,2.4m風洞大型飛機試驗結果的不確定度水平為：UCL約為 0.005～0.006,UCD約為0.0005～0.0009,UCm約為0.003～0.004,相對量分別為1%～4%,1.5%～2.0%,而俯仰力矩系數相對不確定度一般為2%左右,但在巡航姿態附近,模型處于縱向配平狀態其俯仰力矩很小,因而其相對不確定度偏大。

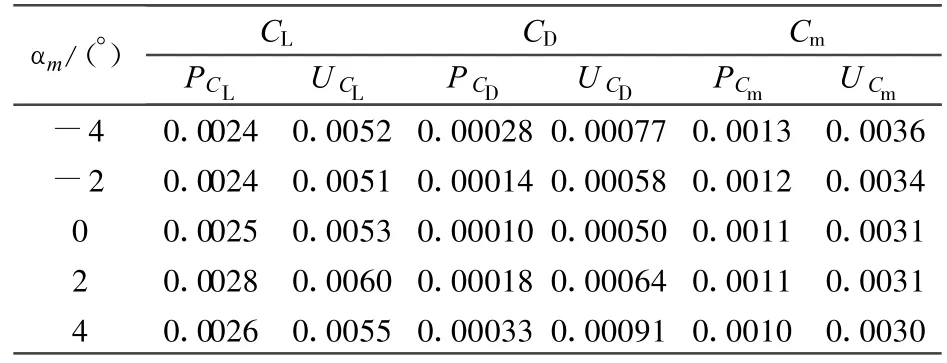
表3 某大型飛機試驗結果不確定度分析T able 3 The uncertainty calculation results of certain large aircraft

2.2 試驗結果不確定度的影響因素分析

圖2分別給出縱向3個氣動力(矩)系數不確定度的主要影響因素,均以百分比的形式給出。其中,UX、UY、UMz分別是天平阻力元 、升力元 、俯仰力矩元測量不確定度的影響量;UP0、UPc、UM分別是總壓和靜壓測量不確定度以及M數控制精度的影響量;Uαm、Upw、Usjd分別是名義迎角、平尾安 裝角、升降舵安裝角的不確定度影響量。

從圖2(a)中可以看出,在較小迎角時升力系數不確定度中名義迎角的影響最大,高達80%,天平Y元的影響在小角度時約占15%左右。主要原因是大型飛機升力線斜率較大,甚至達到0.15/(°),0.01°量級的迎角不確定度將引起0.001量級的升力系數不確定度,而在小迎角時升力系數值較小,其它因素影響并不顯著。迎角大于4°以后,其它因素的影響變大,如總、靜壓測量不確定度,以及模型的振動影響等,影響量約在10%～25%之間。

從圖2(b)中可以看出,零度迎角附近天平阻力元測量不確定度對阻力系數不確定度影響最大,接近80%;在中等迎角時名義迎角的影響逐漸增大,在4°附近與阻力元影響量相當,各約占35%;在較大迎角時,天平Y元和靜壓測量的不確定度等影響增大,各占10%～15%左右,此時,M數控制精度影響量最大。主要原因包括兩個方面,一是迎角很大以后模型相對試驗段的堵塞度很大,給流場M數建立帶來很大困難,同時洞壁干擾等影響也增大;另一方面,此時模型繞流以大面積分離流為主,流動非定常性影響變大,也成為影響試驗結果不確定度的重要因素;而馬赫數影響因子(靈敏度系數)是通過不同馬赫數試驗結果插值得到的,因而這些因素的影響就通過M數的不確定反映出來。

圖2(c)給出俯仰力矩系數不確定度的主要影響因素,可以看出在整個迎角范圍內,天平俯仰力矩元以及平尾安裝角誤差都是最主要的影響因素,分別在40%和30%左右;迎角不確定度在小角度時約15%左右,升降舵安裝角的不確定度影響最大接近10%。

圖2 縱向氣動力(矩)系數不確定度影響因素Fig.2 The uncertainty influence of the longitudinal aerodynamic coefficient

此外,計算結果表明,天平及支桿的彈性角對縱向數據的影響主要體現在中等迎角,對升力系數最大影響量約15%,而對阻力和俯仰力矩系數的最大影響量為10%左右。

某大型飛機縱向試驗數據的不確定度分析結果表明：除個別點的升力系數外,2.4m跨聲速風洞大型飛機試驗數據精度能夠滿足××標準[5]的要求;其影響大型飛機試驗數據質量的主要因素是天平測量不確定度、模型姿態的不確定度、總、靜壓測量不確定度以及模型活動舵面安裝定位誤差等。因此,提高試驗結果的質量,尤其是型號設計部門最為關心的巡航狀態試驗結果的質量,目前最主要的是應減小迎角定位和天平測量的不確定度水平。同時,在較大迎角時,則總、靜壓測量的不確定度、天平彈性角修正的不確定度、振動影響等因素均起較大的作用,它們對試驗質量的影響規律及抑制手段都還需要進行深入的研究。

3 結 論

對建立2.4m跨聲速風洞大型飛機試驗質量評估體系進行了初步探索,標定了風洞基本參數的不確定度水平,完善了以AGARD方法為基礎的不確定度評估方法,編制出評估軟件。對某大型飛機試驗結果的不確定度評估分析表明,該風洞縱向試驗結果的不確定度水平為：UCL約為0.005～0.006,UCD約為0.0005～0.0009,UCm約為 0.003～0.004,試驗結果的不確定度約為精度極限的2～4倍。認為影響小迎角升力、阻力系數試驗質量的最主要因素是迎角控制及天平測量不確定度,而俯仰力矩系數的不確定度中,平尾的安裝定位精度也起主要的作用。這些方面都是今后提高2.4m跨聲速風洞大飛機試驗質量應努力的方向。

[1] 陳作斌.風洞實驗質量評估[M].(譯自AGA RD AR-304).CARDC,1995.

[2] 李建強,張平,王義慶等.風洞數據不確定度分析方法[J].空氣動力學報,2000,18(3)：300-306.

[3] LARRY A M.A new method for integrating uncertainty analysis into data reduction software[R].AIAA 98-0632,1998.

[4] 黃勇,錢豐學,董立新.基于符號計算的風洞試驗數據不確定度評估[J].流體力學實驗與測量,2002,16(3)：91-95.

[5] 惲起麟.風洞實驗[M].北京：國防工業出版社,2000.