大轉角超低展弦比擴壓葉柵流場數值模擬及分析

嚴 明 ，焦廣云 ，魏 然

（北京航空航天大學，1.航空發動機氣動熱力重點實驗室；2.能源與動力工程學院，北京，100191）

隨著現代航空工業的飛速發展,航空發動機的性能需要進一步提高。其中，壓氣機性能的改善，對整個發動機起著至關重要的作用。因此，如何提高壓氣機的性能，成了目前世界各國共同關注的重要研究領域之一。許多研究者都嘗試了對葉型進行改造，借此來提高壓氣機壓比和效率，有效地減小或消除附面層分離。

由于加大了對氣流的轉折能力，所以大轉角靜子葉柵內流動分離加劇，葉型損失增加。超低展弦比葉柵流動，受端壁附面層影響嚴重，最終造成較大的二次流損失。壓氣機中二次流損失與葉柵端壁和葉片表面附面層有關,如端區附面層中摩擦造成的損失、葉片表面附面層潛移引起的低能氣體堆積造成的損失、通道渦造成的漩渦耗散損失等。二次流損失越大，總壓損失越大，而總壓損失系數沿葉高分布總是葉根、葉尖兩端高，葉中低。這樣，在設計時，要想減少端區的總壓損失的話，需控制徑向流動，使高能氣體輸運到端壁，降低端區的能量損失，提高端區總壓。國內外專家學者的實驗研究成果證明：采用傾斜、彎曲葉片，能明顯降低葉柵能量損失。因此，本文設計了7種葉型葉柵并對其進行CFD模擬，通過計算結果，對比分析各個葉型葉柵的氣動性能。

1 幾何模型

本文共研究7個葉型葉柵，分別是：常規直葉柵（葉根到葉尖均勻加載），正傾斜葉片葉柵，直葉柵（外端壁前加載，內端壁后加載），直葉柵（葉中前加載，端區后加載），端區正彎曲葉柵，串列葉柵，直葉柵（葉根到葉尖全部前加載）。為方便起見，將其依次編號為：0型，1型，2型，3型，4型，5型，6型。下文中的敘述，將都采用這種編號方式。這7種葉型都具有大轉角、超低展弦比的特點，轉角為55°，展弦比為0.199。葉高0.0055m，弦長0.0276m。具體三維葉型如圖1。

圖1 0～6型葉片三維葉型

2 計算網格及初場邊界條件

計算網格利用其旋轉對稱性，只對一個葉片進行數值計算，網格利用Autogrid軟件生成，具體參數如表1所示。

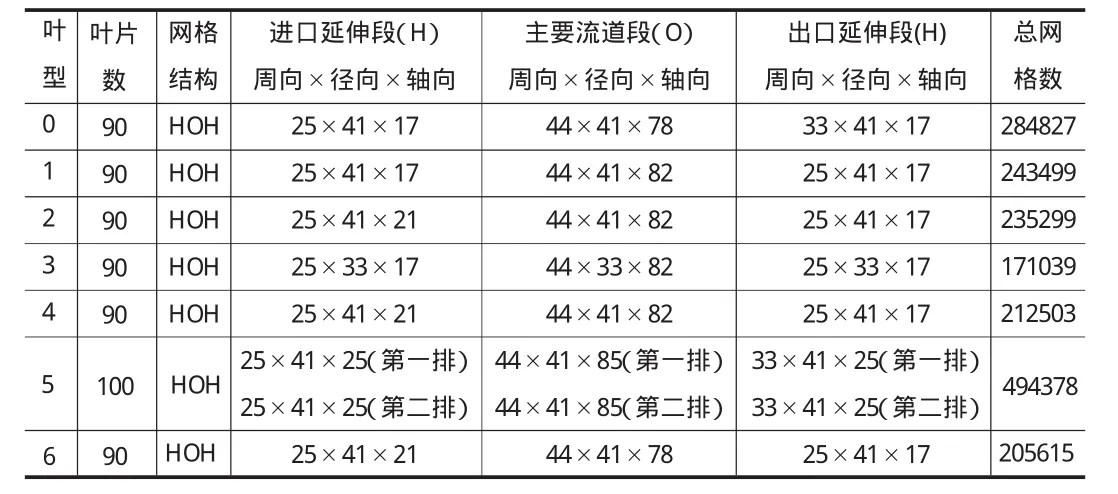
表1 各葉型網格參數設置

初場設為靜壓1.064MPa，靜溫300 K；進口邊界條件給定來流速度，軸向速度75m/s，周向速度106.18m/s，切向速度為0；出口給定背壓1.064MPa；葉片表面為無滑移邊條，兩邊界面為周期性邊條。

3 計算結果及分析

本文計算采用FINE軟件完成，為方便起見，計算結果均以0型為參照，分析如下：

3.1 靜壓增壓比分析

表2 各葉型葉柵靜壓增壓比

從表2可以看出，相對于0型，2型和4型有小幅提高，6型提高最大，1型、3型、5型有較大幅度降低。從這個參數來看，6型最好。

3.2 落后角分析

表3 各葉型葉柵落后角

從表3可以直接看出，6型葉柵平均落后角最小，相對0型減少了42.5%，3型相對于0型也有減少，減少了18.2%，6型減少的幅度較小，而2、4、5型葉柵平均落后角都有不同程度增加。從這個參數來看，6型最好。

3.3 流動損失分析

流動的能量的損失體現在總壓損失上，用總壓恢復系數σ=p2*/p1*來衡量損失的大小，本文中各葉型總壓損失系數如表4所示：

表4 總壓恢復系數

從表4可以看出，6型葉柵總壓損失最小，5型葉柵總壓損失最大。下面取每個葉型沿葉根到葉尖方向0.05倍葉高、0.5倍葉高、0.95倍葉高3個截面的馬赫數分布和吸力面馬赫數分布觀察分離和損失情況，如圖2所示。

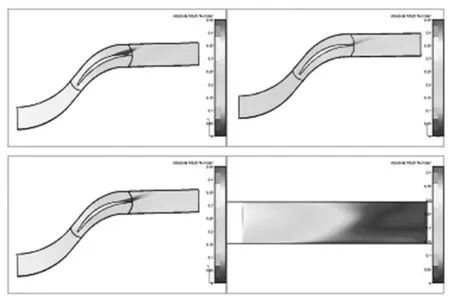
圖2 0型葉片沿葉高0.05、0.5、0.95截面處及吸力面馬赫數分布

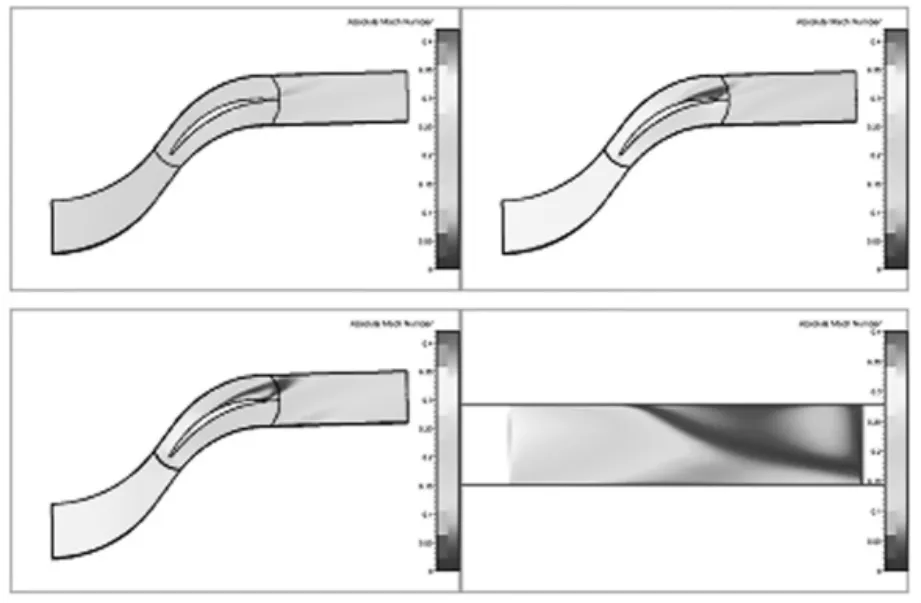
圖3 1型葉片沿葉高0.05、0.5、0.95截面處及吸力面馬赫數分布

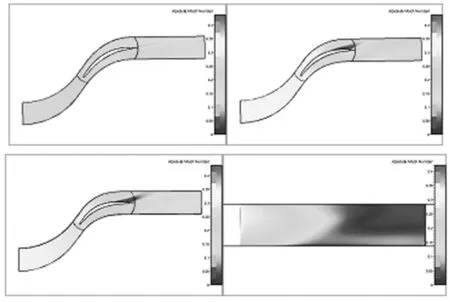
圖4 2型葉片沿葉高0.05、0.5、0.95截面處及吸力面馬赫數分布

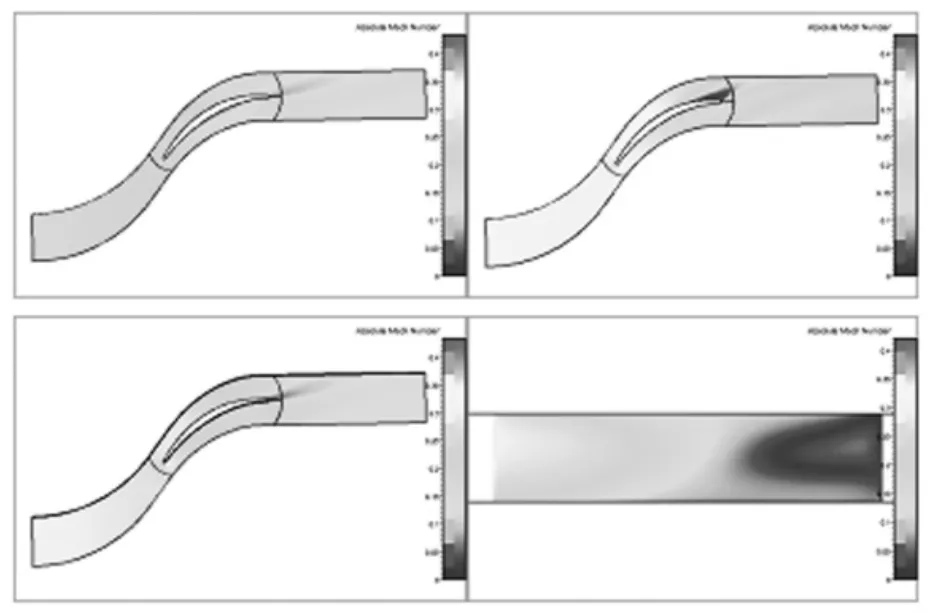
圖5 3型葉片沿葉高0.05、0.5、0.95截面處及吸力面馬赫數分布

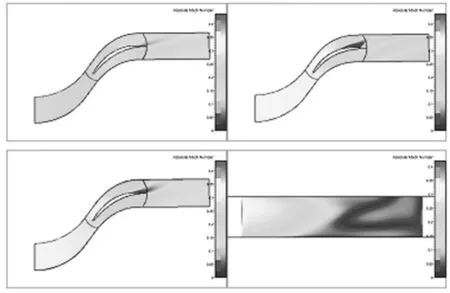
圖6 4型葉片沿葉高0.05、0.5、0.95截面處及吸力面馬赫數分布

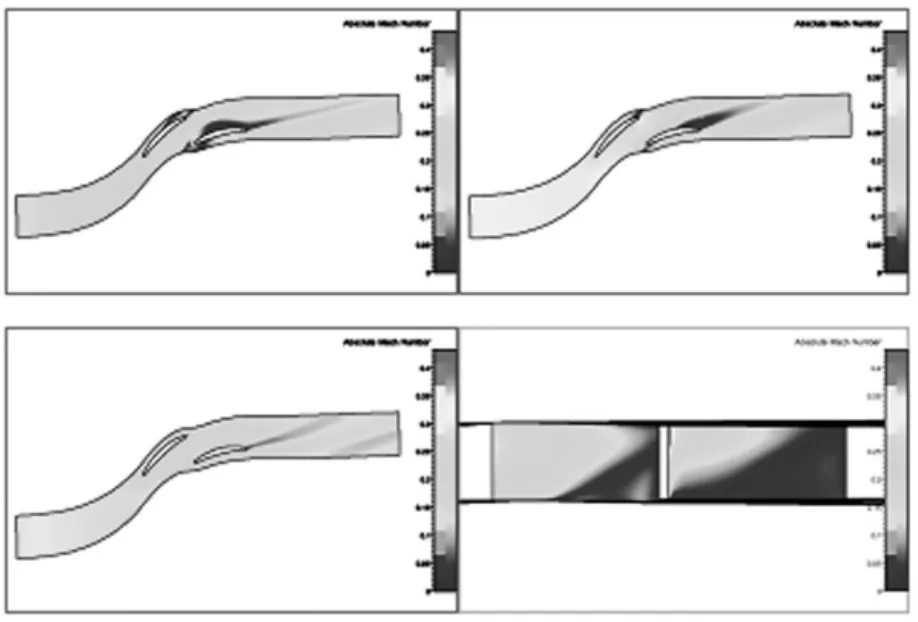
圖7 5型葉片沿葉高0.05、0.5、0.95截面處及吸力面馬赫數分布

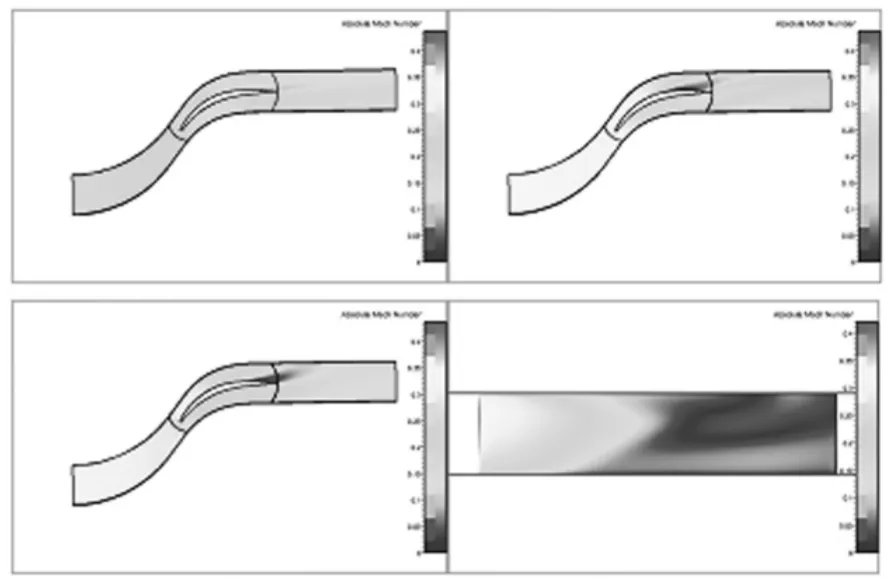
圖8 6型葉片沿葉高0.05、0.5、0.95截面處及吸力面馬赫數分布

對比圖2和圖3可以看出，0型內外端壁分離區域較大，1型內端壁有明顯改善，外端壁處分離稍加強，葉中處分離區域變大。結合吸力面馬赫數分布來分析，可以看出分離發生之后，0型外端壁速度高，葉中速度低，使得附面層向葉中堆積，葉中處損失嚴重。再分析1型可發現，1型發生分離較早，內端壁處馬赫數比葉中高，這樣的話，內端壁附面層會向葉中遷移，同時發現內端壁至葉中區域速度梯度大，輸運的能力較強，所以，低能氣體在葉中至外端壁處堆積，該區域流動損失加劇，而葉中至內端壁區域流動情況有所改善。

對比圖2和圖4可以看出，2型內端壁分離情況明顯改善，外端壁至葉中處分離稍有所加強。分析吸力面馬赫數分布可看出，在靠近內端壁區域，下側馬赫數高，上側馬赫數低，這樣會造成低能氣體由內端壁向葉中方向輸送，這種趨勢比0型要明顯，所以在靠近內端壁區域2型分離區小，流動損失少。2型外端壁至葉中方向為負馬赫數梯度，并且該處梯度比0型要大，所以2型低能氣體向葉中方向輸運的效果要明顯，導致外端壁至葉中區域流動損失加大。

對比圖2和圖5可以看出，3型內外端壁分離情況都有所改善。3型在整個流向上，呈現內外端壁壓力高、葉中壓力低的分布，即外端壁至葉中和內端壁至葉中，均為正馬赫數梯度。在這種馬赫數梯度下，內外端壁的低能流體向葉中遷移，兩端區流動損失減少，葉中處流動損失加大。而在接近出口處可發現，馬赫數分布逐漸變成兩端區低，葉中高。在一定程度上使得低能氣體向兩端壁遷移，反映到總壓分布上，便是葉中區域總壓損失大，兩端區稍有損失。

對比圖2和圖6可以看出，4型內端壁處分離情況均有所改善。4型兩端區附近壓力分布，都是兩端區馬赫數高，附近區域馬赫數低。這種分布趨勢，比0型明顯，所以兩端區分離情況得以改善，流動損失減小，葉中損失增大。在接近出口的一段區域里，葉中馬赫數比兩端區壓力高，低能流體向兩端遷移。

對比圖2和圖7的吸力面馬赫數分布可知，5型下端壁分離情況嚴重，分離發生的較早，第二排葉柵從前緣至尾緣幾乎全部分離，外端壁至葉中處摻混比較均勻，所以此區域流動損失減小的幅度比較小，相對而言，內端壁至葉中區域損失較大。

對比圖2和圖8可以看出，6型內端壁分離情況改善明顯，外端壁處分離情況無明顯改變，葉中分離稍有加強。6型與3型的馬赫數分布相似，同樣是內端壁區域，分離情況得到改善，流動損失減少，外端壁區域分離的比較早，流動損失增大。但總體上來看，6型總壓損失比0型小。這與3型總壓損失比0型大有所差異的地方在于：6型為前加載葉型，在未出現附面層分離時，加載葉型損失小，使得總體損失減小。內端壁處分離區較大，葉中處分離區域稍小，外端壁處分離區很小。

4 結束語

本文通過對7種大轉角、超低展弦比葉型葉柵的靜壓增壓比，落后角和流動損失的分析，得出了以下結論，相對于常規直葉柵（葉根到葉尖均勻加載）：

（1）正傾斜葉型內端壁處附面層分離情況改善明顯，但外端壁至流動損失增加。總體看來，落后角增大，總壓損失增大，靜壓增壓比減小。

（2）外端壁前加載、內端壁后加載葉型內端壁附面層分離情況改善，外端壁附面層分離情況加劇。總體看來，落后角增大，總壓損失也增大，靜壓增壓比增大。

（3）端區正彎葉型改善了內外端區附面層分離情況。綜合來看，落后角增大，出口總壓損失略有增大，靜壓增壓比減小。

（4）葉中前加載、端區后加載葉型，使得兩端區附面層分離情況略有改善。葉中處低能氣體先堆積后遷移，總壓幾乎沒有變化。總體來講，總壓損失減小，落后角增大，靜壓增壓比略有增大。

（5）串列葉柵分離區集中在內端壁至葉中處，但由于內端壁處分離發生的較早，前緣至尾緣幾乎全部分離，所以內端壁至葉中處處摻混比較均勻。總體說來落后角減小，總體損失增大，靜壓增壓比降低。

（6）葉根到葉尖全部前加載葉型二次流加強，葉型損失減少，總體損失減少，落后角減小，靜壓增壓比增大。

綜合以上各個性能參數來看，葉根到葉尖全部前加載葉型性能最好，適合大轉角、超低展弦比葉柵，可為以后的葉型葉柵設計提供一定的參考。

[1]王會社，鐘兢軍，王仲奇，趙 剛.正傾斜葉片壓氣機葉柵二次流的數值研究[J].熱能動力工程，2007，(17)：375-378.

[2]王會社，袁 新，鐘兢軍，王仲奇.葉片正彎曲對壓氣機葉柵葉片表面流動的影響[J].推進技術，2004，25(3)：143-146.

[3]陳紹文，陳 浮，王可立，谷 君，王仲奇.采用彎葉片的不同折轉角壓氣機葉柵流場氣動性能[J].推進技術，2007，28（2）：179-182.

[4]焦廣云.大轉角、超低展弦比擴壓葉柵流場計算與分析[D].北京：北京航空航天大學，2008.