由一道循環小數題引發的思考

■蔡青

由一道循環小數題引發的思考

■蔡青

在小學五年級數學教學中涉及到一個知識點——循環小數。而循環小數又分為純循環小數和混循環小數。有這么一道題：“0．3103103103……是（）小數，可簡記為（），循環節是（）。”我認為解決這道題的關鍵是要正確理解一個概念——循環節，因為對于一個循環小數，判斷它是純循環小數還是混循環小數，是根據這個循環小數的循環節的起點位置來確定的。循環節從小數點后第一位開始出現的就是純循環小數，不是從小數點后第一位開始出現的就是混循環小數。

而循環節到底該如何確定，在許多教師中存在爭議。就拿這一題來說，有的老師說：“0．3103103103．…．…是一個混循環小數，簡寫為0．3103,循環節是103。”理由是：循環節在最后不可能出現半個循環節，它只能以整循環節的形式出現，書上循環小數的例子很多，如教材（第九冊）第28頁：3．33……，6．416416……，15．438438……都是這樣，還沒有哪一個說出現半邊循環節的。打個比方說：循環節就像自行車上的鏈條，是一節一節的，是一環套一環的，不可能出現半節鏈條。而有的教師認為：“0．3103103．10．3……是一個純循環小數，簡寫為0．310,循環節是310。”理由是：它的循環節是從小數點后第一位開始出現的，最后出現的并不是一個完整的循環節，這恰恰是出題者設置的陷阱，再說，書上并沒有明文規定說循環節必須以整循環節的形式出現。

一時間，這兩種對立的看法爭執不下，因為這兩種觀點的理由都不足以說服對方。那么，到底誰對誰錯呢？為了搞清楚這個問題，我們還是先看看循環節的定義：“一個循環小數的小數部分中依次重復出現的一個或幾個數字叫做循環節。”定義中并沒有明文規定究竟以哪一個數字為起點，因此出現爭議。根據定義，0．3103103103……的循環節可以是310，也可以是103，還可以是301310。為了避免引起混亂，一般采取把小數中最先按一定順序重復出現的那一個數字定為循環節的起點，并將重復出現的最少位數定為一個循環節。也就是說，確定循環節的位置需要附加兩個標準：“最先”和“最少”。所以，0．3103103103…．…．是一個純循環小數，可以簡記為0．310，循環節是310。第一種觀點違反了“最先”這一標準，因而不正確。

當然，我們還可以通過分數與循環小數的互化來證明這一點。首先，我們把這個小數化成分數。

①如果按第一種觀點，把這個小數按混循環小數化成分數，過程如下：

（分子為小數點后第一個數字到第一個循環節末的數字組成的數減去非循環數字組成的數所得的差，分母由“9”和“0”組成，“9”的個數為循環節的位數，“0”的個數為非循環部分的位數。）

②如果按第二種觀點，把這個小數按純循環小數化成分數，過程如下：

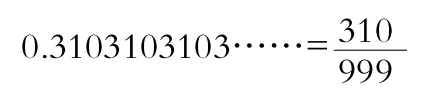
（分子為循環節，分母由“9”組成，“9”的個數為循環節的位數。）

顯然，兩種結果一樣，說明它只符合一種情況。到底是哪種情況呢？我們通過一個定理來加以判斷。定理：一個最簡分數，它的分母只含有2和5以外的質因數時，它所化的小數是純循環小數；若分母既含有質因數2和5，又含有2和5以外的質因數，它所化的小數是混循環小數。根據輾轉相除法可以知道，是一個最簡分數，其分母999=3× 3×3×37。所以，0．3103103103……是一個純循環小數。

通過這一題我們可以看出，它是循環小數中的一個特例。事實上，在數學各知識點中，特例是普遍存在的，如“四舍五入”法在特殊情況下卻有四入五舍，相背而行的行程問題是相遇問題中的特例等。作為數學老師，我們應該實事求是，客觀地面對數學中的特例，絕對不能單憑主觀臆斷而誤人子弟。

武漢市新洲區汪集街馮鋪小學）

任編輯 廖林